
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

363
9 Kurven
Die Steuerung von Industrierobotern ist ein typisches Anwendungsbeispiel für Kurven. Ein anderes Beispiel sind Spiralkurven, mit denen Daten auf CDs geschrieben oder von CDs gelesen werden. Bahnkurven von Satelliten werden ebenfalls durch Kurven beschrieben. Ganz allgemein erzeugen eindimensional bewegte Objekte eine Bahnkurve. Der Begri „eindimensional“ bedeutet dabei, dass sich das Objekt auf einer gekrümmten Kurve nur in eine Richtung bewegt. Bereits vor einigen Jahrhunderten beschäftigten sich Mathematiker mit der Beschreibung der Bahnkurven von Himmelskörpern. Nach Angaben von Daniel Kehlmann hat sich Carl Friedrich Gauß selbst in seiner Hochzeitsnacht mit solchen Fragen beschäftigt.
In diesem Kapitel betrachten wir unterschiedliche Darstellungsformen von ebenen Kurven und Raumkurven. Wir werden mit Mitteln der Di erenzialund Integralrechnung Formeln zur Berechnung von Tangenten, Krümmungen und Bogenlängen von Kurven angeben. Die elementaren ebenen Kurven wie Kreise, Ellipsen und Hyperbeln betrachten wir ausführlich.
9.1 Parameterdarstellung
Das Schaubild einer Funktion stellt eine ebene Kurve dar. Solche Kurven nennt man Kurven in expliziter Form. Der Begri Kurve ist jedoch viel allgemeiner gefasst. In Abschnitt 5.1.4 haben wir bereits gesehen, dass ein Vollkreis nicht als Schaubild einer Funktion dargestellt werden kann. Der Vollkreis kann jedoch durch eine implizite Gleichung dargestellt werden. Man spricht dann von einer Kurve in impliziter Form. Doch selbst manche einfache Kurve, wie beispielsweise eine Spirale, lässt sich weder als Kurve in expliziter Form noch als Kurve in impliziter Form vernünftig darstellen. Zur mathematischen Beschreibung von Kurven verwendet man deshalb die sogenannte Parameterdarstellung. Kurven bezeichnen wir, genau wie Vektoren, mit fettgedruckten Kleinbuchstaben. Die Koordinaten beziehen sich auf ein kartesisches Koordinatensystem, siehe Definition 3.17.
Definition 9.1 (Parameterdarstellung einer Kurve)
Bei der Parameterdarstellung einer Kurve hängen die Koordinaten der Kurvenpunkte als Funktionen von einem reellen Parameter t ab:
|
|
|
|
|
|
|
x t |
|
|
|
|
c t |
y t |
) |
, |
t I, |
c t |
’ |
y |
(t) |
“ |
, |
t I. |
( ) = Π|
x t |
‘ |
|
( ) = – |
|
( ) — |
|
|
|||
( |
|
|
|||||||||
|
( ) |
|
|
|
” |
|
( ) • |
|
|
||
Ebene Kurven haben zwei Koordinatenfunktionen x(t) und y(t). Raumkurven werden durch drei Koordinatenfunktionen x(t), y(t) und z(t) beschrieben.

364 |
9 Kurven |
Eine Kurve ist erst durch Angabe der Koordinatenfunktionen und des Parameterintervalls festgelegt. Der Parameter durchläuft das komplette Intervall und erzeugt so die Punkte der Kurve. Jede einzelne Koordinatenfunktion muss auf dem kompletten Parameterintervall definiert sein. In der Regel fordert man, dass alle Koordinatenfunktionen stetig sind. Dadurch entstehen lückenlose Kurven. Die Welt der Parameterwerte und die Welt der Koordinaten ist vollkommen getrennt. Man kann sich vorstellen, dass sich die Parameterwerte auf einer Art Zeitskala bewegen und zu jedem Zeitpunkt einen Kurvenpunkt erzeugen.
Beispiel 9.1 (Einheitskreis) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
a) |
Durch die Parameterdarstellung |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
t = |
1 |
π |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
c(t) = Π|
cos t |
|
‘ , |
|
t 0, |
3 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
sin t |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t = π |
|
|
|
|
|
|
|
|
|
|
|
|
t = 0 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|||||||||||||||||||||||||||||||
|
wird eine ebene Kurve dargestellt. Die Kurve |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
startet |
für |
t |
|
0 im |
|
|
Punkt |
|
mit |
|
den Koordina- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = |
3 |
π |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
ten |
|
1 0 |
|
und endet für t |
|
|
3 |
π im Punkt mit |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Koordinaten |
|
|
|
|
|
1 . Alle Punkte liegen auf |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
den ( |
S |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dem Einheitskreis, denn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 π 2 π |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( S − ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
t |
|
|||||||||||||||||||||
|
x |
|
t |
2 |
|
y |
|
t |
2 |
|
|
|
cos2 t sin2 t |
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Die implizite( ) + (Gleichung) = |
|
x+2 |
|
|
y2 |
=1 reicht nicht aus, um den Dreiviertelkreis genau festzule- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
gen. Man benötigt eine mathematische Beschreibung, aus der hervorgeht, dass nur ein Teil |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
des Vollkreises gemeint ist. Den Dreiviertelkreis kann man nicht als Schaubild einer einzi- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
gen Funktion darstellen. Bei einer Funktion darf jeder y-Wert höchstens zu einem x-Wert |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
gehören. Man kann sich dadurch behelfen, dass man den oberen und den unteren Halbkreis |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
jeweils getrennt durch eine Funktion beschreibt: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
, x |
|
|
|
|
|
|
1, 1 |
|
|
|
|
|
|
|
|
√ |
|
|
|
|
, x |
|
|
|
1, 0 . |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
f1 |
|
x |
|
|
|
1 |
|
|
x2 |
|
|
|
|
|
|
|
, |
|
|
|
f2 |
|
x |
1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
b) |
|
|
( |
|
) = + |
|
|
− |
|
|
|
|
|
|
|
|
|
|
[− |
|
|
|
] |
|
|
|
|
|
( ) = − |
− |
|
|
|
|
|
[−y |
|
|
] |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Alternativ kann man für den Dreiviertelkreis die |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
t = 2 π |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Parameterdarstellung |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = 23 π |
|
|
|
|
|
|
|
|
|
|
|
|
t = 25 π |
|
|
|
|
|||||||||||||||||||||||||
|
c(t) = Π|
sin t |
|
‘ , |
|
t π, |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
cos t |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|||||||||||||||||||||||||||||
|
wählen. Die Kurve startet für t |
|
π im Punkt mit |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = π |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
den Koordinaten |
|
|
0 |
|
|
|
|
1 und endet für t |
|
|
5 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
im Punkt mit den Koordinaten |
|
1 0 . Dadurch |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
S − |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ändern sich der Durchlaufsinn und der Anfangs- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 π t |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( S ) |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
2 π |
|
||||||||||||
|
und Endpunkt. Nach wie vor wird jedoch dersel- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
be Ausschnitt des Einheitskreises dargestellt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
c) |
Der Einheitskreis lässt sich auch durch die Parameterdarstellung |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
c(t) = |
1 |
Œ 1−2tt2 ‘ , |
|
|
|
|
t R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
mithilfe rationaler Funktionen repräsentieren. Die Koordinatenfunktionen erfüllen die Kreis- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
gleichung für alle Parameterwerte t: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x t |
2 |
|
y |
|
t |
2 |
|
|
|
|
|
|
|
4t2 |
|
|
|
|
|
|
|
1 t2 2 |
|
4t2 1 2t2 t4 |
1 2t2 t4 |
|
1 t2 2 |
|
1. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t2 2 |
|
|
|
|
(1 |
|
|
|
t2 2 |
|
|
|
|
+1 |
t2 2 |
|
|
|
|
|
1 t2 2 |
|
|
|
|
|
t2 2 |
|
|
|
|
|||||||||||||||||
|
|
( ) + ( ) = |
( |
+ ) |
|
|
+ |
− ) |
= |
|
|
|
− + |
= |
+ + |
|
|
|
|
= |
(1 + ) |
= |
|
|
Ì |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
( |
|
+ ) |
|
|
|
( + ) |
|
|
|
( + ) |
|
|
|
( + ) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
9.1 Parameterdarstellung |
365 |
Parameterdarstellung
Unterschiedliche Parameterdarstellungen können ein und dieselbe Kurve erzeugen. Eine Kurve besitzt keine eindeutige Parameterdarstellung.
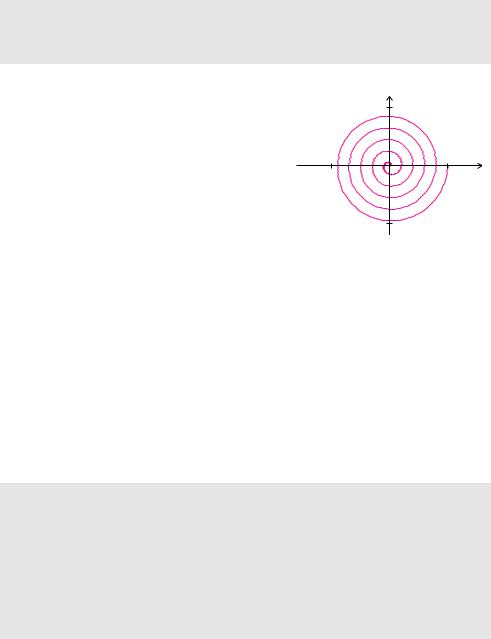
Beispiel 9.2 (Archimedische Spirale) |
|
Bei der nach dem griechischen Mathematiker Archi- |
y |
medes benannten Spirale verändert sich der Radius |
2 nπ |
|
|
proportional zum Winkel. Dadurch haben die einzel- |
|
nen Windungen immer denselben Abstand zueinan- |
|
der. Die Kurve wird durch die Parameterdarstellung |
|
−2 nπ |
2 nπ x |
cos t |
|
c(t) = t Œ sin t ‘ , t [0, 2 n π] , |
|
beschrieben. Jedes Mal, wenn der Parameter t ein |
−2 nπ |
Intervall der Länge 2π durchläuft, bewirken cos t |
|
und sin t eine volle Umdrehung. Dabei wird der Vorfaktor t um den Wert 2π vergrößert. Mithilfe der Tangente, siehe Abschnitt 9.3, kann man zeigen, dass die Spirale den Ursprung in Richtung der positiven x-Achse verlässt. Ì
Archimedische Spiralen finden in Verdichtern ihre Anwendung. In zwei gegenläufigen Spiralen wird durch Rotation das eingeschlossene Volumen verkleinert und so der Druck erhöht. Dieses Prinzip wird etwa in Turboladern, Kompressoren und Wärmepumpen eingesetzt.
Die Kurve aus Beispiel 9.2 ist typisch für Kurven in sogenannten Polarkoordinaten. Eine ebene Kurve definiert man in Polarkoordinaten dadurch, dass man jedem Kurvenpunkt einen Rotationswinkel ϕ und einen entsprechenden Radius r zuordnet. Polarkoordinaten sind insbesondere im Zusammenhang mit komplexen Zahlen von Bedeutung, siehe Definition 11.5.
Definition 9.2 (Ebene Kurve in Polarkoordinaten)
In der Darstellung einer ebenen Kurve
c |
t |
|
r |
t |
|
cos ϕ t |
|
, |
t |
|
I |
|
) = |
) Π|
sin ϕ |
(t) |
‘ |
|
|||||||
|
( |
|
( |
|
( ) |
|
|
|
||||
bezeichnet man ϕ(t) und r(t) als Polarkoordinaten. Dabei ist ϕ eine Funktion, die jedem Parameterwert t aus dem Intervall I einen Winkel ϕ(t) zuordnet, und r(t) eine Funktion, die jedem t aus I einen nicht negativen Radius r(t) zuordnet.
Die Darstellung einer Kurve in Definition 9.2 basiert auf einem kartesischen Koordinatensystem, siehe Definition 3.17. Man kann jedoch die Polarkoordinaten auch direkt in einem Polarkoordinatensystem einsetzen. Dann sind ϕ(t) und r(t) die beiden Koordinatenfunktionen.
366 |
9 Kurven |
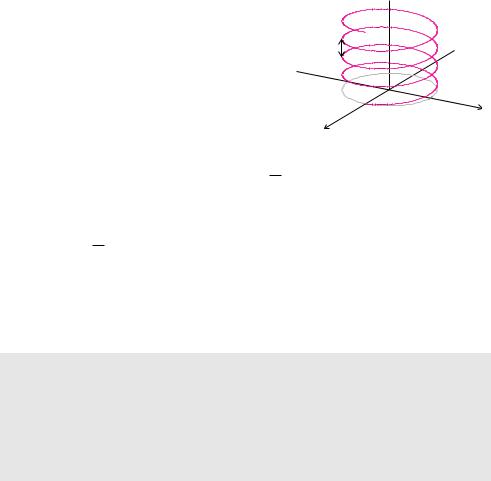
Beispiel 9.3 (Schraubenlinie)
Wir suchen eine Parameterdarstellung der Schraubenlinie mit Grundkreisradius r und Ganghöhe h. Ausgangspunkt für unsere Überlegungen ist eine Parameterdarstellung des Kreises mit Mittelpunkt (0 S 0 S 0) und Radius r in der x-y-Ebene
’ r cos t “ c0(t) = – r sin t — .
” 0 •
In der z-Koordinate müssen wir dafür sorgen, dass wir pro Umdrehung die Höhe h gewinnen.
z 
c(t)
h
r y
r
xc0(t)
Bei linearem Anwachsen gelingt dies durch z(t) = 2hπ t. Das Parameterintervall bestimmt die Anzahl der Umdrehungen. Insgesamt erhalten wir für n volle Umdrehungen
c |
t |
’ |
r cos t |
“ |
, |
t |
[ |
0, 2 n π |
] |
. |
Ì |
r sin t |
|||||||||||
|
( |
) = – |
|
— |
|
|
|
|
|
”2hπ t •
Das Schaubild einer Funktion f für x-Werte im Intervall I kann man als Spezialfall einer ebenen Kurve interpretieren. Dazu interpretiert man die x-Werte als Parameterwerte und die Funktionswerte als y-Werte der Kurve. Alle Formeln für parametrisierte Kurven lassen sich dadurch auf Schaubilder von Funktionen übertragen.
Schaubild einer Funktion als ebene Kurve
Das Schaubild einer Funktion f für x-Werte in einem Intervall I lässt sich als ebene parametrisierte Kurve c(t) darstellen:
c(t) = Π|
t |
‘ , t I. |
f(t) |
9.2 Kegelschnitte
Die einfachsten echt gekrümmten ebenen Kurven sind die sogenannten Kegelschnitte. Sie umfassen Kreise, Ellipsen, Hyperbeln und Parabeln. Anschaulich definiert man einen Kegelschnitt als Schnittkurve zwischen einer Ebene und einem Kegel. Im Zusammenhang mit Kegelschnitten verstehen wir hier unter einem Kegel eine Fläche, die man umgangssprachlich als unendlich ausgedehnten Doppelkegel bezeichnen würde. Der Typ der Kurve ist abhängig vom Schnittwinkel zwischen der Ebene und den Mantellinien.
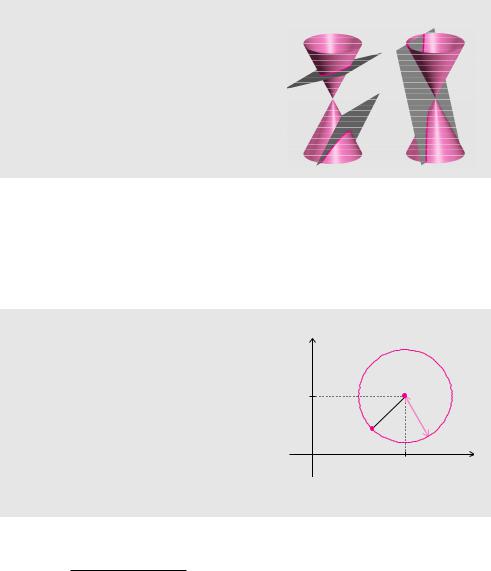
9.2 Kegelschnitte |
367 |
Definition 9.3 (Kegelschnitt)
Eine Schnittkurve zwischen einer Ebene und einem Kegel bezeichnet man als Kegelschnitt. Insbesondere sind Kreise, Ellipsen,
Hyperbeln und Parabeln Kegelschnitte. In Spezialfällen bestehen die Schnittkurven aus Geraden oder entarten zu einem Punkt. Der Typ des Kegelschnitts ist vom Winkel zwischen Ebene und Mantellinien abhängig.
Kegelschnitte lassen sich aber auch über geometrische Eigenschaften definieren. Beispielsweise besagt die geometrische Definition des Kreises, dass ein Kreis aus allen Punkten besteht, die denselben Abstand von einem Mittelpunkt haben. Schließlich kann man Kegelschnitte auch noch durch quadratische Gleichungen definieren. Der Einheitskreis besteht beispielsweise aus allen Punkten, die die Gleichung x2 + y2 = 1 erfüllen. Wir werden bei der Darstellung der Kegelschnitte alle diese Aspekte aufgreifen.
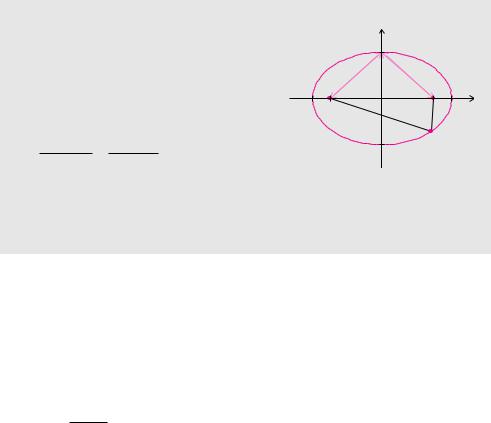
Definition 9.4 (Kreis)
Ein Kreis mit Radius r > 0 besteht aus allen Punkten P (x S y), die denselben Abstand r vom Mittelpunkt M(x0 S y0) haben. Die Punkte erfüllen die Gleichung
(x − x0)2 + (y − y0)2 = r2.
Eine Parameterdarstellung lautet
c |
t |
|
x0 |
r cos t |
|
, t |
|
0, 2 π |
|
. |
) = Π|
y0 |
+ r sin t |
‘ |
[ |
) |
|||||
|
( |
|
+ |
|
|
|
y |
|
|
|
|
M(x |
| y ) |
|
y |
0 |
0 |
|
0 |
|
|
|
|
|
r |
|
|
P(x| y) |
|
|
|
x |
|
x |
|
0 |
|
|
Die Gleichung in Definition 9.4 kann man direkt aus der Abstandsformel aus Satz 3.16 herleiten. Der Punkt P (x S y) hat vom Mittelpunkt M(x0 S y0) den Abstand
»
r = (x − x0)2 + (y − y0)2.
Die Gültigkeit der Parameterdarstellung in Definition 9.4 kann man durch Einsetzen in die Gleichung nachweisen:
(x0 + r cos t − x0)2 + (y0 + r sin t − y0)2 = r2(cos2 t + sin2 t) = r2.
Wählt man für den Parameter t nicht ein komplettes Intervall der Länge 2 π, so kann man auf elegante Weise Teile des Vollkreises darstellen. Intervalle mit einer Länge größer als 2 π führen dazu, dass Teile des Kreises mehrfach durchlaufen werden. Auch der Durchlaufsinn der Kurve kann leicht verändert werden, indem man beispielsweise t durch −t ersetzt.
368 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 Kurven |
|||||
Beispiel 9.4 (Kreis) |
|
|
|
|
|
|
|
|
|
|
) |
|
(− |
|
S |
|
) |
||
Wir bestimmen die Gleichung des Kreises mit Mittelpunkt M 1 |
2 |
, der durch den Punkt P |
1 |
0 |
|||||||||||||||
geht. Die beiden Punkte P und M haben den Abstand |
( S |
|
|
|
|
||||||||||||||
|
» |
|
|
√ |
|
2√ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1 1 2 |
2 2 |
|
|
|
|
|
|
|
|
|
|
|||||||
r |
8 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
Dieser Abstand= (−ist− der) |
Radius+ (− ) des= |
gesuchten= |
Kreises. Somit hat der Kreis die Gleichung |
|
|
|
|
|
|||||||||||
(x − 1)2 + (y − 2)2 = 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
||||
Definition 9.5 (Ellipse)
Eine achsenparallele Ellipse mit den Halbachsen a > 0 und b > 0 besteht aus allen Punkten P (x S y), bei denen die Summe der Abstände zu den Brennpunkten F1 und F2 den konstanten Wert 2a hat. Die Punkte erfüllen die Gleichung
|
( |
x |
− |
x0 |
) |
2 |
+ |
|
( |
y |
− |
y0 |
) |
2 |
= |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
a2 |
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|||
Eine Parameterdarstellung lautet |
|
|
|
|
|||||||||||||||||
c |
t |
|
|
|
x0 |
|
|
a cos t |
|
|
, t |
|
0, 2 π |
|
. |
||||||
) = Π|
y0 |
+ b sin t |
‘ |
[ |
) |
||||||||||||||||
|
|
( |
|
|
+ |
|
|
|
|
|
|
|
|||||||||
|
|
y |
|
|
|
b |
|
|
a |
a |
|
|
F |
F |
|
−a |
1 |
2 |
|
−e |
e |
a x |
|
|
|
P(x| y) |
|
|
|
−b |
|
Die Herleitung der Gleichung aus Definition 9.5 erfolgt durch Aufsummieren der Abstände, die ein Punkt von den beiden Brennpunkten hat. Den konstanten Wert 2a erkennt man im Punkt P (0 S b). Die Gültigkeit der Parameterdarstellung erfolgt wie beim Kreis durch Einsetzen in die Gleichung. Wir verzichten jedoch auf die einzelnen algebraischen Umformungen. Bei einer Ellipse bezeichnet man den Abstand der beiden Brennpunkte zum Mittelpunkt als Exzentrizität e. Die Exzentrizität ist ein Maß dafür, wie stark eine Ellipse von einem Kreis abweicht. Eine Ellipse mit Exzentrizität e = 0 ist ein Kreis. Zwischen den Halbachsen a, b und der Exzentrizität e besteht nach dem Satz von Pythagoras der Zusammenhang
√
e = a2 − b2.
Landschaftsgärtner erzeugen Ellipsen, indem sie an den Positionen der Brennpunkte zwei Pflöcke einschlagen und eine Schnur der Länge 2 a daran befestigen. Bewegt man nun eine Markierung entlang der stets gespannten Schnur, so erhält man eine Ellipse.
9.2 Kegelschnitte |
|
|
|
|
|
|
369 |
|||
Beispiel 9.5 (Ellipse) |
|
|
|
|
|
|
||||
Die Parameterdarstellung |
|
|
|
|
|
|
||||
c |
t |
|
8 |
6 cos t |
|
, |
t |
|
0, 2 π |
|
) = Π|
6 + |
4 sin t |
‘ |
[ |
) |
|||||
|
( |
+ |
|
|
|
|
||||
beschreibt eine Ellipse mit dem Mittelpunkt M(8 S 6) und den Halbachsen a = 6 und b = 4. Wir möchten nun entscheiden, ob der Punkt P (12 S 3) innerhalb, außerhalb oder genau auf der Ellipse liegt. Dazu betrachten wir die Mittelpunktsgleichung
(x − 8)2 + (y − 6)2 = 1 62 42
und setzen die Koordinaten des Punktes P ein:
( |
12 |
− |
8 |
2 |
+ ( |
3 |
− |
6 |
) |
2 |
|
16 |
9 |
|
145 |
> |
||||
|
|
) |
|
|
= |
|
+ = |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
62 |
|
|
|
|
|
42 |
|
|
|
36 |
16 |
144 |
Ì |
||||
Der Punkt P liegt also außerhalb der Ellipse. |
||||||||||||||||||||
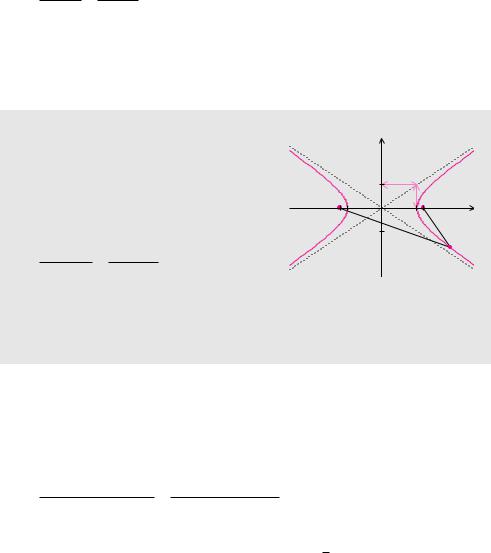
Definition 9.6 (Hyperbel)
Eine achsenparallele Hyperbel mit den Parametern a > 0 und b > 0 besteht aus allen Punkten P (x S y), bei denen die Di erenz der Abstände von den beiden Brennpunkten F1 und F2 den konstanten Wert 2a hat. Die Punkte erfüllen die Gleichung
(x − x0)2 − (y − y0)2 = ±1. a2 b2
|
y |
|
|
|
|
b |
a |
|
|
F1 |
b |
F2 |
|
|
|
|
|||
|
|
|
||
−e −a |
|
a |
e |
x |
−b |
|
|
|
|
|
|
|
|
|
|
|
P(x| y) |
|
|
Eine Parameterdarstellung lautet
c t |
|
x0 |
a cosh t |
|
, |
t |
|
R. |
) = Π|
y0 |
± b sinh t |
‘ |
|
||||
( |
|
± |
|
|
|
Die unterschiedlichen Vorzeichen in den Formeln gehören zu den unterschiedlichen Hyperbelästen. Ein Hyperbelast kann nach links, rechts, oben oder unten geö net sein. Die Herleitung der Gleichung aus Definition 9.6 erfolgt aus der Di erenz der Abstände, die ein Punkt von den beiden Brennpunkten hat. Auch hier verzichten wir auf die Details. Die Gültigkeit der Parameterdarstellung erfolgt durch Einsetzen in die Gleichung und mithilfe von Satz 5.22:
( |
x |
± |
a cosh t |
− |
x |
0) |
2 |
− |
( |
y |
0 |
± |
b sinh t |
− |
y |
0) |
2 |
= cosh2 t − sinh2 t = 1. |
0 |
a2 |
|
|
|
b2 |
|
|
|||||||||||
|
|
|
|
|
|
Charakteristisch für Hyperbeln sind ihre Asymptoten. Die beiden Asymptoten schneiden
sich im Mittelpunkt M(x0 S y0) und haben die Steigung ± b . a
370 |
|
|
|
|
|
|
|
|
|
|
9 Kurven |
Beispiel 9.6 (Hyperbel) |
|
|
|
|
|
||||||
Die Parameterdarstellung |
|
|
|
|
|
||||||
c |
t |
) = Π|
3 |
+ |
2 cosh t |
‘ |
, |
t |
|
R |
|
− |
1 |
4 sinh t |
|||||||||
|
( |
|
+ |
|
|
|
|
||||
beschreibt eine Hyperbel. Die x-Werte werden nicht kleiner als 5. Es wird also nur der rechte Ast definiert. Die Asymptoten haben die Steigungen ±2 und schneiden sich im Punkt M(3 S − 1). Die Hyperbel besitzt die Gleichung
(x − 3)2 − (y + 1)2 = 1.
22 42
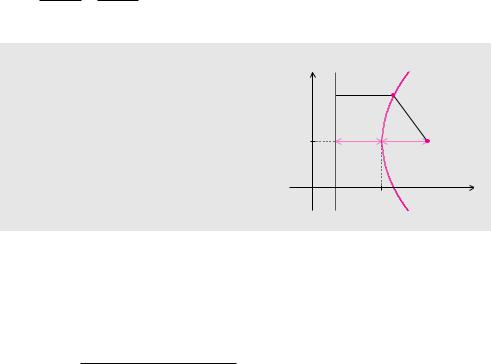
Definition 9.7 (Parabel)
Eine achsenparallele Parabel besteht aus allen Punkten P (x S y), bei denen der Abstand zum Brennpunkt F und zur Leitlinie ` gleich groß ist, wobei der Parameter p > 0 den Abstand zwischen F und ` beschreibt. Die Punkte erfüllen eine Gleichung der Form
y |
y0 |
|
2 |
= |
2p |
x |
x0 |
|
(x |
− x0) |
|
2 |
±2p |
(y |
− y0 ) |
||
( |
− |
) |
|
= |
± |
( |
− ) |
|
Ì
y |
` |
|
|
|
P(x| y) |
||
|
|
||
y0 |
p |
p |
|
2 |
2 |
F |
|
|
x0 |
|
x |
Der Parameter p wird manchmal auch als Halbparameter bezeichnet, da in der Parabelgleichung der Ausdruck 2p steht. Die unterschiedlichen Vorzeichen in den Formeln gehören zu den unterschiedlichen Parabelästen. Ein Parabelast kann nach links, rechts, oben oder unten geö net sein. Für die Herleitung der Gleichung aus Definition 9.7 betrachten wir den Fall einer nach rechts geö neten Parabel. Der Punkt P (x S y) hat den Abstand d1 = x − x0 + p2 von der Leitlinie `. Der Abstand zwischen dem Punkt P (x S y) und dem Brennpunkt beträgt
¾
|
p |
2 |
||
d2 = ‹x − ‹x0 + |
•• + (y − y0)2. |
|||
|
|
|||
2 |
|
|||
Da die beiden Abstände d1 und d2 gleich sind, folgt
‰x − x0 + p2 Ž2 = ‰x − x0 − p2 Ž2 + (y − y0)2 Ô 2 p (x − x0) = (y − y0)2 .
Die drei anderen Fälle ergeben sich durch ähnliche Betrachtungen. Die Eigenschaften von Parabeln werden in der Technik für Parabolspiegel ausgenutzt. Bei einem Parabolspiegel werden parallel einfallende Strahlen im Brennpunkt gebündelt. Umgekehrt erzeugt eine punktförmige Lichtquelle durch einen Parabolspiegel paralleles Licht in eine Richtung.
Kreise, Ellipsen, Hyperbeln und Parabeln werden alle durch quadratische Gleichungen in x und y beschrieben. Man kann zeigen, dass auch umgekehrt jede quadratische Gleichung in x und y einen Kegelschnitt beschreibt. In entarteten Fällen können, zusätzlich zu Kreisen, Ellipsen, Hyperbeln und Parabeln, auch Geraden oder Punkte entstehen.
9.2 Kegelschnitte |
371 |
Satz 9.1 (Kegelschnittgleichung)
Jeder Kegelschnitt kann durch eine quadratische Gleichung der Form a x2 + 2 b x y + c y2 + 2 d x + 2 e y + f = 0
beschrieben werden. Umgekehrt beschreibt jede quadratische Gleichung einen Kegelschnitt. Für b = 0 verlaufen die Achsen parallel zu den Koordinatenachsen und man kann den Typ des Kegelschnitts aus den Vorzeichen der restlichen Koe zienten bestimmen:
L |
Kreis |
a |
= |
c 0 |
≠ 0 |
|
L |
Ellipse |
a c |
0 |
Parabel |
c |
0, a, e |
oder |
Hyperbel |
< |
0 |
||||
L |
a |
= |
0,≠ c, d |
0 |
L |
a c > |
||||
|
|
|
= |
|
≠ |
|
|
|
|
|
Die Kegelschnittgleichung enthält an mehreren Stellen den Faktor 2. Durch diese Schreibweise werden weitere Formeln für Kegelschnitte einfacher. Für b ≠ 0 ist die Typbestimmung von Kegelschnitten etwas aufwendiger. Das liegt daran, dass die Hauptachsen für b ≠ 0 nicht parallel zu den Koordinatenachsen verlaufen. Man kann zeigen, dass die Achsen um einen Winkel α gegenüber den Koordinatenachsen gedreht sind, mit
tan (2 α) = 2b . a − c
Beispiel 9.7 (Kegelschnittgleichungen)
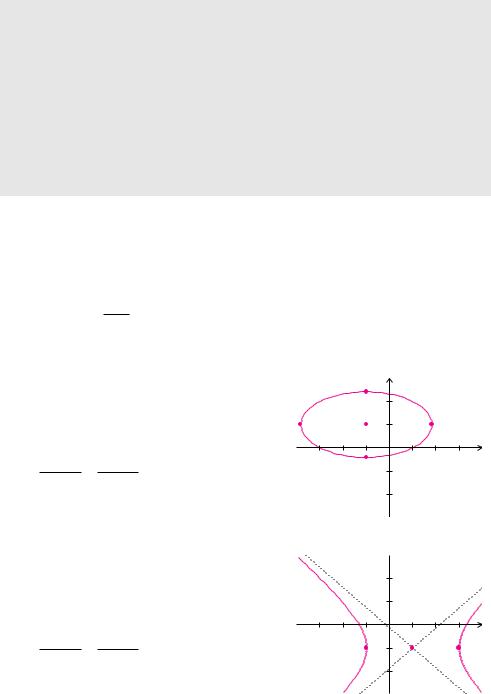
a) Ein Kegelschnitt wird beschrieben durch:
x2 + 4y2 + 2x − 8y − 3 = 0
Durch quadratische Ergänzung der Terme in x und y erhalten wir
(x + 1)2 + (y − 1)2 = 1.
82
Der Kegelschnitt ist also eine Ellipse mit dem
Mittelpunkt M |
1 |
|
1 |
|
und den beiden Halbach- |
|||||||
sen |
|
|
|
|
|
(− S |
|
) |
|
|
|
|
|
a |
= |
√ |
|
= √ |
|||||||
|
|
2 2 und b |
|
|
|
2. |
||||||
|
|
y |
|
|
S4 |
2 |
|
S1 |
M |
1 |
S2 |
−3 |
1 2 3 x |
S3 −1
−2
b) Zur Bestimmung des Typs der Gleichung
3x2 − 4y2 − 6x − 8y − 13 = 0
ergänzen wir die Terme in x und y jeweils zu vollständigen Quadraten:
(x − 1)2 − (y + 1)2 = 1.
43
Damit ist der Kegelschnitt eine Hyperbel mit
dem Mittelpunkt M 1 |
√ |
1 und den beiden Pa- |
||||
|
= |
|
= |
|
|
|
rametern a |
b |
3.) |
||||
|
2 und ( S − |
|||||
y
2
1
−3 −2 −1 |
1 2 3 x |
S1 −1 |
S2 |
−2 |
M |
|
