
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
98 |
3 Vektoren |
3.4 Punkte, Geraden und Ebenen
Mit der Vektorrechnung lassen sich weit mehr Probleme lösen, als wir bisher betrachtet haben. Beispielsweise kann man den Abstand, den ein Punkt von einer Ebene hat, oder den Schnittwinkel zwischen zwei Ebenen mithilfe von Vektoren berechnen. In diesem Abschnitt beschäftigen wir uns mit dem Zusammenhang von Vektoren mit Punkten, Geraden und Ebenen. Wir verwenden die Vektorrechnung, um geometrische Probleme zu lösen. In der Mathematik bezeichnet man dieses Teilgebiet als analytische Geometrie. Oftmals fällt die Trennung zwischen Vektoren einerseits und Punkten, Geraden und Ebenen andererseits nicht leicht. Punkte haben eine feste Position im Raum, Vektoren sind jedoch frei verschiebbar. Vektoren besitzen eine endliche Länge, Geraden und Ebenen sind mathematische Gebilde, die in ihrer Ausdehnung unbeschränkt sind.
3.4.1 Kartesisches Koordinatensystem
Die Grundlage für das Rechnen mit Punkten, Geraden und Ebenen bilden räumliche kartesische Koordinatensysteme, benannt nach dem Franzosen René Descartes.
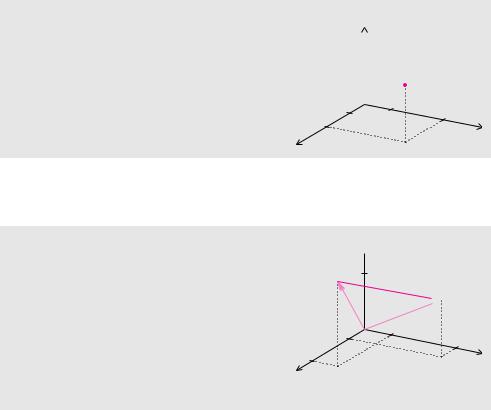
Definition 3.17 (Kartesisches Koordinatensystem im Raum)
Ein Achsenkreuz aus drei paarweise senkrech- |
z |
|
|
|
|
|
|||||||||
ten Geraden, die sich im Ursprung O schnei- |
z0 |
|
|
|
P0(x0|y0|z0) |
|
|||||||||
|
|
|
|
||||||||||||
den, nennt man ein kartesisches Koordina- |
|
|
|
|
|
||||||||||
tensystem. Die Einheitslängen sind auf allen |
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||
drei Achsen gleich und die Einheitsvektoren in |
1 |
|
|
O |
1 |
|
|
||||||||
Richtung der Geraden bilden ein Rechtssystem. |
|
|
y0 |
y |
|||||||||||
|
|
|
|
||||||||||||
x0 |
|
|
|
||||||||||||
Ein Punkt P0 |
( |
x0 |
S |
y0 |
S |
z0 |
) |
wird durch seine Ko- |
x |
|
|
|
|
|
|
ordinaten beschrieben. |
|
|
|
|
|
|
|
|
|
||||||
Der Zusammenhang von Punkten und Vektoren ergibt sich durch Ortsvektoren und Verbindungsvektoren.
Definition 3.18 (Ortsvektor und Verbindungsvektor)
Den Vektor a vom Punkt P1 (x1 S y1 S z1) zum Punkt P2 (x2 S y2 S z2) nennt man den Verbindungsvektor. Er hat die Koordinaten
’ x2 − x1 “
a = – y2 − y1 — .
” z2 − z1 •
Ein Ortsvektor ist ein Verbindungsvektor vom Ursprung O (0 S 0 S 0) zu einem Punkt.
P1 
xx1
z  z2
z2
O x2
a
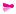 P2
P2
y1
y2 y

3.4 Punkte, Geraden und Ebenen |
99 |
Für die Koordinatendarstellung von Punkten und Vektoren verwenden wir bewusst unterschiedliche Schreibweisen. Die Koordinaten von Vektoren stellen wir in einer Spalte dar, die Koordinaten von Punkten werden durch einen vertikalen Strich getrennt in einer Zeile dargestellt.
Beispiel 3.17 (Vektor zwischen zwei Punkten)
Der Vektor a vom Punkt A(3 S − 4 S 4) zum Punkt B(1 S − 2 S 5) hat die Koordinaten
|
’ |
1 |
− |
3 |
“ ’ |
2 |
“ . |
|
a |
2 |
4 |
−2 |
|
||||
|
= – −5 |
+ |
4 |
— = – |
1 |
— |
Ì |
|
|
” |
|
− |
|
• ” |
|
• |
|
Wenn man in der Mathematik vom Abstand spricht, dann meint man damit den kürzesten Abstand. Der Abstand zweier Punkte entspricht der Länge des Verbindungsvektors. Diese Länge berechnen wir nach Satz 3.10.
Satz 3.16 (Abstand zwischen Punkten)
Die Punkte P1 (x1 S y1 S z1) und P2 (x2 S y2 S z2) haben den Abstand
¼
dP1 P2 = (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2.
Der Punkt P (x S y S z) hat vom Ursprung den Abstand
»
dP = x2 + y2 + z2.
Beispiel 3.18 (Teilung einer Strecke)
Die Strecke zwischen dem Punkt P (5 S 8 S 1) und dem Punkt Q(−4 S 2 S − 2) soll durch den Punkt M im Verhältnis 1 zu 2 geteilt werden. Welche Koordinaten hat der Punkt M? Wir berechnen zunächst den Verbindungsvektor a von P nach Q:
|
|
|
4 |
− |
5 |
9 |
“ . |
a |
’ −2 |
8 |
“ ’ −6 |
||||
|
= – |
− |
2 |
− |
1 |
— = – −3 |
— |
|
” |
|
− |
|
• ” − |
• |
|
Den Ortsvektor m des Punktes M erhalten wir dann aus dem Ortsvektor p des Punktes P und dem Verbindungsvektor a durch
|
|
|
|
1 |
|
|
5 |
|
1 |
9 |
|
2 |
|
|
m |
|
p |
|
a |
’ |
8 |
“ |
’ −6 |
“ ’ |
6 |
“ . |
|||
= |
+ |
|
+ |
|
||||||||||
|
|
|
|
= – |
|
— |
|
– − |
— = – |
|
— |
|||
3” 1 • 3 ” −3 • ” 0 •
Der Punkt M hat somit die Koordinaten M(2 S 6 S 0). |
Ì |
100 |
3 Vektoren |
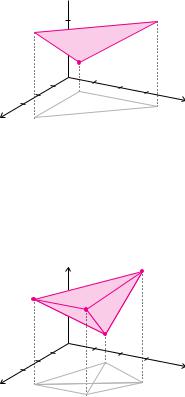
Beispiel 3.19 (Flächeninhalt eines Dreiecks)
Die drei Punkte P (1 S 1 S 1), Q(4 S 1 S 3) und R(1 S 4 S 3) bilden ein Dreieck. Zur Berechnung des Flächeninhalts verwenden wir den Verbindungsvektor a von P nach Q, den Verbindungsvektor b von P nach R und bestimmen den Vektor c = a × b:
a |
’ |
3 |
“ |
, |
b |
’ |
0 |
“ |
, |
c |
6 |
“ . |
x |
0 |
3 |
’ −6 |
|||||||||||
|
= – |
2 |
— |
|
|
= – |
2 |
— |
|
|
= – −9 |
— |
|
|
” |
|
• |
|
|
” |
|
• |
|
|
” |
• |
|
z 
 R
R
Q 
|
P |
|
|
|
1 |
1 |
2 |
|
|
|
3 |
y |
||
2 |
|
|
3
Den Flächeninhalt des Dreiecks A erhalten wir aus dem Betrag des Vektors c:
|
A |
= |
|
1 |
S |
c |
S = |
1 |
» |
|
|
|
6 |
|
2 |
|
|
6 |
|
2 |
|
|
92 |
= |
3√17 . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
(− |
|
|
) |
|
+ (− ) + |
|
|
|
|
|
|
|
|
|
Ì |
|||||||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||
Beispiel 3.20 (Volumen eines Tetraeders) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Die |
vier |
Punkte |
P |
( |
4 |
S |
3 |
S |
3 , |
Q |
( |
4 |
S |
1 |
S |
3 |
) |
, |
R |
( |
2 |
S |
4 |
S |
4 |
) |
z |
|
R |
|||||||||||
und |
|
|
S |
|
) |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
Q |
|
P |
|||||||||||||||
des |
S 1 |
2 |
1 |
bilden ein Tetraeder. Zur Berechnung |
|
|
|
|||||||||||||||||||||||||||||||||
( S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Volumens verwenden wir den Verbindungsvektor |
|
|
|
||||||||||||||||||||||||||||||||||||
a von P nach Q, den Verbindungsvektor b von P
nach R und den Verbindungsvektor c von P nach S: |
|
|
1 |
S |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
’ |
0 |
“ |
|
|
2 |
“ |
|
|
3 |
“ . |
|
|
2 |
3 |
y |
|
|
|
|
|
|
|
2 |
|
|
|||||||||
a |
2 |
, |
b |
’ −1 |
, |
c |
’ −1 |
x |
3 |
|
|
|
|
||||
|
= – −0 |
— |
|
|
= – 1 |
— |
|
|
= – −2 |
— |
|
|
|
|
|
|
|
|
” |
|
• |
|
|
” |
• |
|
|
” − |
• |
|
|
|
|
|
|
Das Volumen des Tetraeders erhalten wir dann aus dem Spatprodukt dieser Vektoren:
|
|
1 |
|
|
1 |
|
|
7 |
|
|
||
V |
= |
|
T [ |
a, b, c |
] T = |
|
S − |
14 |
S = |
|
|
Ì |
6 |
|
|
||||||||||
|
|
6 |
|
3 . |
||||||||
3.4.2 Parameterdarstellung von Geraden und Ebenen
Geraden und Ebenen besitzen zwei verschiedene Darstellungsformen: Eine Form mit und eine ohne Parameter. Jede der beiden Formen hat Vorund Nachteile. In diesem Abschnitt starten wir mit der Parameterdarstellung von Geraden und Ebenen. Die Darstellung ohne Parameter sind Thema des nächsten Abschnitts.

3.4 Punkte, Geraden und Ebenen |
101 |
Definition 3.19 (Punktrichtungsform einer Geraden)
Eine Gerade g kann durch einen Richtungsvek- |
|
||||
tor a |
≠ |
0 und durch einen Punkt P mit dem |
P |
||
|
0 |
0 |
0 |
||
Ortsvektor x festgelegt werden: |
|||||
|
|
||||
|
g |
x = x0 + λ a, λ R. |
|
|
|
a
x 0
P |
g |
|
x
O
Bei der Parameterdarstellung der Geraden g in Definition 3.19 ist die Gleichung so zu interpretieren, dass die Gerade g aus allen Punkten P mit Ortsvektor x besteht, bei der sich der Ortsvektor x in Form von x = x0 + λa darstellen lässt. Der Parameter λ wirkt als eine Art Schieberegler. Für λ = 0 erhalten wir den sogenannten Aufpunkt P0. Mit wachsenden λ-Werten erhalten wir Punkte, die von P0 aus in Richtung des Vektors a verlaufen. Negative λ-Werte erzeugen diejenigen Punkte, die in entgegengesetzter Richtung liegen. Der Parameter λ durchläuft alle reellen Zahlen. Dadurch werden alle Punkte auf der Geraden durch einen eindeutigen Parameterwert λ beschrieben. In ähnlicher Weise lässt sich eine Gerade auch durch zwei Punkte festlegen. Dabei übernimmt der Verbindungsvektor der beiden Punkte die Rolle des Richtungsvektors.
Definition 3.20 (Zweipunktform einer Geraden)
Eine Gerade g kann durch zwei verschiedene Punkte P0 und P1 mit den Ortsvektoren x0 und x1 festgelegt werden:
g x = x0 + λ (x1 − x0) , λ R.
P0
x 0
P1
x
1
P |
g |
|
x
O
Zur Definition einer Ebene benötigt man zwei Richtungen, genauer gesagt, zwei linear unabhängige Vektoren. Jede Richtung wird unabhängig durch einen eigenen Parameter gesteuert.
Definition 3.21 (Punktrichtungsform einer Ebene)
Eine Ebene E kann durch zwei linear unabhängige Richtungsvektoren a und b und durch einen Punkt P0 mit dem Ortsvektor x0 festgelegt werden:
E x = x0 + λ a + µ b, λ, µ R.
Die Parameter λ und µ sind unabhängig voneinander.
b
P |
|
|
0 |
x |
|
x |
||
|
||
0 |
|
P a
O
E
