
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

15.2 Eigenschaften |
575 |
Darstellung mit Amplitude und Phase
Die Fourier-Transformierte einer reellen Funktion s ist in der Regel eine komplexwertige Funktion S, die von der reellen Variablen f abhängt. Man kann S in Exponentialform
S(f) = SS(f)S ei φ(f)
darstellen. Dabei ist
»
Ldie Amplitude SS(f)S = R(f)2 + I(f)2 eine gerade reelle Funktion und
Ldie Phase φ(f) = arg(S(f)) = arg(R(f) + i I(f)) eine ungerade reelle Funktion.
Beispiel 15.6 (Darstellung mit Amplitude und Phase)
Aus der Fourier-Transformierten |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
S(f) = 1 |
1 |
|
|
|
|
|
|
|
− |
2 π f |
|
|
|
|
|
|
|
| |
S(f) |
| |
|
||||||||
4π2f2 + i |
1 |
4π2f2 |
|
|
|
|
1 |
|
|
|
|||||||||||||||||||
der Funktion |
s t+ |
|
e |
− |
t |
σ t |
|
|
|
+ |
|
|
|
|
|
3 |
2 |
1 |
1 |
|
2 |
3 |
t |
||||||
|
( ) = |
|
|
|
( ) |
aus Beispiel 15.3 erhal- |
− |
− |
− |
|
|
|
|
||||||||||||||||
ten wir die |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Amplitude |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
S f |
|
|
»1 |
|
4 |
2 |
2 |
|
|
|
|
|
2 |
2 |
|
|
π |
|
|
|
|
|
|||||||
S ( )S = |
|
|
|
|
|
π2 f2 |
= »1 |
|
|
|
|
|
|
2 |
|
φ(f ) |
|
|
|||||||||||
1 |
|
+4 π f |
|
|
+ |
4 π f |
|
|
|
|
|
|
|
|
|
||||||||||||||
und die Phase |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
−2 |
−1 |
1 |
|
2 |
3 |
f |
||||||
φ |
( |
f |
) = − |
arctan |
( |
2 π f |
) |
. |
|
|
|
|
|
|
|
−π2 |
|
|
|
|
Ì |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
15.2 Eigenschaften
Die Fourier-Transformationen einfacher Funktionen sind in Tabellen festgehalten, siehe Anhang A.7. Für viele Funktionen kann man deshalb die Fourier-Transformierte berechnen ohne dabei auf die Integralformel aus Definition 15.1 zurückzugreifen. Dazu kombiniert man die Korrespondenzen aus den Tabellen und die Rechenregeln der Fourier-Transfor- mation.
Die Rechenregeln der Fourier-Transformation haben alle eine ähnliche Struktur. Sie geben Aufschluss darüber, wie sich Veränderungen an der Funktion im Zeitbereich auf die Funktion im Frequenzbereich auswirken oder umgekehrt. Typische Veränderungen, die wir betrachten, sind Addition, Multiplikation, Verschiebung, Ableitung und Integration.
576 |
15 Fourier-Transformation |
15.2.1 Linearität
Die Linearität der Fourier-Transformation beinhaltet zwei Aspekte. Zum einen besagt sie, dass der Addition von Funktionen im Zeitbereich die Addition der entsprechenden FourierTransformierten im Frequenzbereich entspricht. Zum andern entspricht der Multiplikation mit einem konstanten Faktor im Zeitbereich die Multiplikation mit demselben Faktor im Frequenzbereich.
Satz 15.4 (Linearität)
Die Addition von Funktionen im Zeitbereich entspricht der Addition der zugehörigen Fourier-Transformierten im Frequenzbereich. Die Multiplikation mit einem konstanten Faktor im Zeitbereich entspricht der Multiplikation mit demselben Faktor im Frequenzbereich.
s1(t), s2(t) |
c |
s |
S1(f), S2(f) |
|
|||
|
× |
|
|
|
|
× |
|
C1 s1 t |
× |
|
|
|
C1 S1 f |
× |
|
×C2 s2 t |
|
|
×C2 S2 f |
||||
|
Ö |
|
c |
s |
|
Ö |
|
C |
+und |
C beliebige Konstanten. |
( ) |
||||
Dabei sind( )1 |
2( ) |
|
|
( |
) + |
||
Der Nachweis der Linearität ist o ensichtlich: Die Linearität der Fourier-Transformation geht aus der Linearität des Integrals hervor.
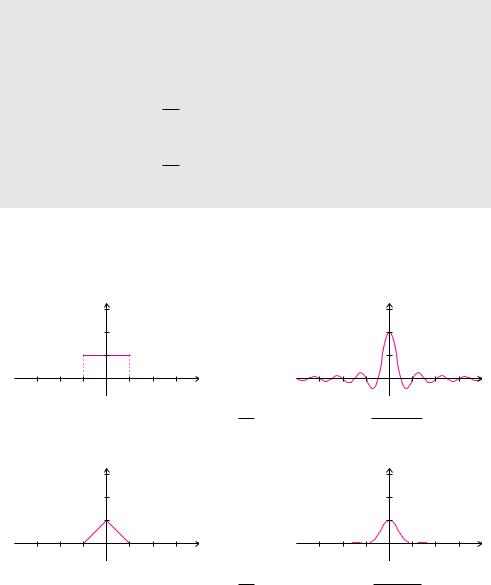
Beispiel 15.7 (Linearität der Fourier-Transformation)
Die Fourier-Transformation der Rechteckfunktion kennen wir bereits aus Beispiel 15.1:
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
s1(t) |
|
|
|
|
|
|
|
|
|
S1(f) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
−3 −2 −1 |
|
1 |
2 |
3 |
t |
|
−3 −2 −1 |
|
1 |
2 |
3 |
f |
|||
|
( |
) |
|
|
c |
s |
|
( |
|
) = |
sin |
2 π f |
) |
|
|
s1 |
|
|
S1 |
f |
( |
|
|
|
|||||||
t |
|
|
|
|
|
|
|
π f |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Die Fourier-Transformation der Dreieckfunktion kann man Beispiel 15.4 entnehmen:
|
2 |
s2(t) |
|
|
|
|
2 |
|
S2(f) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
−3 −2 −1 |
1 |
2 |
3 |
t |
c s |
−3 −2 −1 |
|
1 |
2 |
3 |
f |
|
s2(t) |
|
|
|
S2(f) = |
sin2 |
π f |
) |
|
|
|
|
|
|
|
π2(f2 |
|
|
|||||

15.2 |
Eigenschaften |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
577 |
||
Wir können die Fourier-Transformierte von s1(t) + s2(t) mittels Linearkombination berechnen: |
|||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
˜ |
|
|
|
|||
|
|
|
|
s˜(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(f) |
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
−3 −2 −1 |
1 |
2 |
3 |
t |
|
|
|
−3 −2 −1 |
|
1 |
|
2 |
3 |
f |
||||||
|
s˜ t |
|
s1 t |
s2 t |
|
c |
s |
˜ |
|
|
|
sin 2 π f |
) |
sin2 |
|
π f |
) |
|
|||
|
|
|
S f |
|
|
π f |
π2 f2 |
|
|||||||||||||
|
|
|
|
|
|
|
( |
|
|
|
( |
|
|
( |
|
|
|
||||
|
sich auch die Fourier-Transformierte von s1 |
t |
|
s2 |
t |
ermitteln: |
|
|
|
|
|
|
|||||||||
Ebenso lässt ( ) = |
( ) + |
( ) |
|
|
|
|
|
) = |
|
|
|
+ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
( ) − |
( ) |
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
ˆ |
|
|
|
|||
|
|
|
|
sˆ(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(f) |
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
−3 −2 −1 |
1 |
2 |
3 |
t |
|
|
|
−3 −2 −1 |
|
1 |
|
2 |
3 |
f |
||||||
|
sˆ t |
|
s1 t |
s2 t |
|
c s |
ˆ |
|
|
|
sin 2 π f |
|
sin2 |
|
π f |
|
|
||||
|
|
|
S f |
|
|
π f |
|
2 |
|
2 |
|
|
|||||||||
|
( ) = ( ) − ( ) |
|
|
( ) = |
|
( |
|
) − |
π (f |
|
) |
Ì |
|||||||||
15.2.2 Zeitverschiebung
Als nächstes klären wir die Frage, wie sich eine Verschiebung im Zeitbereich auf die Fourier-Transformation auswirkt. Dazu betrachten wir die um t0 verschobene Funktion
s˜(t) = s(t − t0).
Es sei nochmals darauf hingewiesen, dass t0 |
|
0 eine |
Verschiebung in Richtung der |
|
positiven Zeitachse bewirkt. Entsprechend verschiebt t |
0 |
0 in Richtung der negativen |
||
|
> |
|
|
|
Zeitachse. Die Transformation von s˜ kann man mit der Integralformel aus Definition 15.1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
= |
< |
|
|
|
|
|
|
|
|
|
berechnen. Mithilfe der Substitution u |
t |
t0 und du |
dt ergibt sich |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
˜ |
|
|
|
|
∞ s |
|
|
|
|
− i 2 π f t |
|
|
∞ s |
|
|
|
|
|
i 2 π f u t0 |
|
|
|||
s˜ t |
|
|
|
|
S |
|
f |
|
|
|
t |
|
t0 |
|
e |
dt |
|
|
|
u |
|
e |
|
|
|
du. |
|
||
) |
c s |
( |
) = |
|
( |
− |
) |
= |
|
( |
) |
− |
|
( + ) |
i 2 π f t0 |
||||||||||||||
( |
|
|
S |
−∞ |
|
|
− |
|
S |
−∞ |
|
|
|
|
|||||||||||||||
An den Grenzen |
verändert die Verschiebung um t0 |
nichts. Da der Faktor e− |
|
||||||||||||||||||||||||||
nicht von der Integrationsvariablen u abhängt, können wir diesen Faktor vor das Integral |
|||||||||||
ziehen: |
|
|
|
|
|
±∞ |
|
∞ s u e |
|
|
|
S˜ |
( |
f |
) = |
e |
− |
i 2 π f t0 |
|
− |
i 2 π f udu . |
||
|
|
|
|
S |
−∞ |
( ) |
|
||||
|
|
|
|
|
|
|
|
S f |
|
||
|
|
|
|
|
|
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
||||
|
|
|
|
|
|
|
|
|
( |
|
) |
Wir erkennen, dass es sich bei dem verbleibenden Integral gerade um die Fourier-Trans- formation der Ausgangsfunktion s(t) handelt.
578 |
15 Fourier-Transformation |
Satz 15.5 (Zeitverschiebung)
Die Verschiebung der Funktion s im Zeitbereich um t0 entspricht der Multiplikation der FourierTransformierten S mit dem Faktor e−i 2 π f t0 im Frequenzbereich.
s(t)
×
×
×
Ö
s(t − t0)
c |
s |
|
|
|
S(f) |
|
|
|
||
|
|
|
e |
|
|
× |
S |
|
f |
|
c |
s |
− |
|
× |
( |
) |
||||
|
|
Ö |
|
|
||||||
|
|
|
|
|
i 2 |
π f×t0 |
|
|
|
|
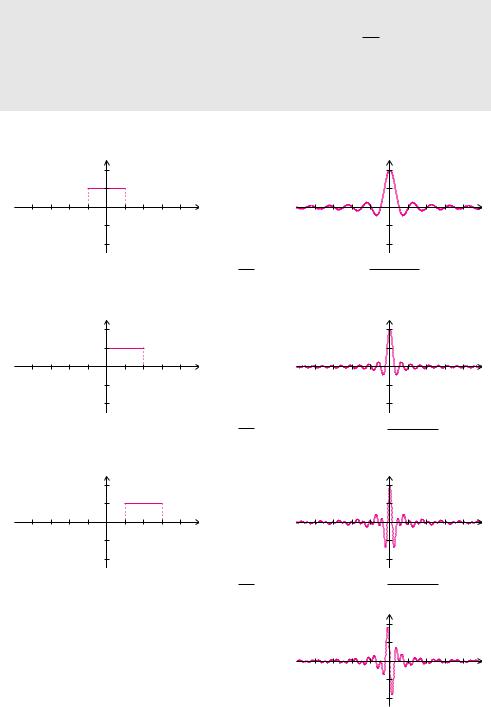
Beispiel 15.8 (Zeitverschiebung bei der Fourier-Transformation)
Die Rechteckfunktion aus Beispiel 15.1 ist gerade, die Fourier-Transformierte ist reell:
2 |
s(t) |
|
|
2 |
S(f) |
1 |
|
|
1 |
||
|
|
|
|
||
−4 −3 −2 −1 |
1 2 3 4 t |
|
|
−4 −3 −2 −1 |
1 2 3 4 f |
−1 |
|
|
|
−1 |
|
−2 |
s(t) |
c |
s |
−2 |
|
|
S(f) = sin(2 π f) |
||||
π f
.
Eine Verschiebung in der Zeit um t0 = 1 bewirkt eine Multiplikation der Fourier-Transformierten mit dem Faktor e−i 2 π f im Frequenzbereich:
|
2 |
|
|
s˜(t) |
|
|
||
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
−4 −3 −2 −1 |
|
1 2 3 4 t |
|
|
||||
−1 |
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
c |
s |
|
s˜ t |
) = |
s |
t |
− |
1 |
) |
||
( |
( |
|
|
|
|
|||
.
|
|
|
|
|
|
2 |
|
˜ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
R(f) |
|
|
|
|
|
|
|
|
|
|
|
−4 −3 −2 −1 |
1 2 3 4 f |
||||||||
|
|
|
|
|
|
−1 |
|
|
|
˜ |
( |
|
) = |
|
− |
−2 |
sin |
2 π f |
) |
|
|
i 2 π f |
|||||||
S |
f |
e |
|
( |
|
||||
π f
Entsprechend bewirkt eine Verschiebung um t0 = 2 eine Multiplikation mit dem Faktor e−i 4 π f :
|
2 |
|
|
sˆ(t) |
|
|
||
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
−4 −3 −2 −1 |
|
1 2 3 4 t |
|
|
||||
−1 |
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
c |
s |
|
sˆ t |
) = |
s |
t |
− |
2 |
) |
||
( |
( |
|
|
|
|
|||
.
Durch die Verschiebung ist die Funktion im Zeitbereich nun nicht mehr gerade und die Fourier-Trans- formierte enthält auch imaginäre Anteile. Hier abge-
ˆ
bildet ist nur I(f).
|
|
|
|
|
2 |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
R(f) |
|
|
|
|
|
|
|
|
|
|
−4 −3 −2 −1 |
1 2 3 4 f |
|||||||
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
−2 |
|
|
) |
ˆ |
|
|
e |
|
i 4 π f sin 2 π f |
|||
S f |
|
|
|
π f |
||||
|
( |
) = |
|
− |
|
|||
|
|
|
( |
|
||||
|
|
|
|
|
2 |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
I(f ) |
|
|
|
|
|
|
|
|
|
|
−4 −3 −2 −1 |
1 2 3 4 f |
|||||||
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
−2 |
|
|
Ì |
|
|
|
|
|
|
|
|
|
