8.2 Potenzreihen und Konvergenz

Potenzreihen sind einerseits Funktionen und andererseits unendliche Reihen. Funktionen sind sie, weil sie von einer Veränderlichen x abhängen. Reihen sind sie, weil jeder einzelne Funktionswert aus einer Summe von unendlich vielen Zahlen besteht.

Definition 8.5 (Potenzreihe)

Eine Funktion p in Form einer unendlichen Reihe mit Koe zienten ak

∞

p(x) = Q ak(x − x0)k = a0 + a1(x − x0) + a2(x − x0)2 + . . . + an(x − x0)n + . . .

k=0

nennt man Potenzreihe mit Entwicklungspunkt x0. Im Spezialfall x0 = 0 ergibt sich

∞

p(x) = Q ak xk = a0 + a1 x + a2 x2 + . . . + an xn + . . .

k=0

Potenzreihen sind bei Weitem nicht so dramatisch, wie sie auf den ersten Blick wirken. Sie besitzen ähnlich angenehme Eigenschaften wie Polynome. Allerdings sind manche Potenzreihen im Gegensatz zu Polynomen nicht für alle reellen Zahlen definiert. Der maximale Definitionsbereich einer Potenzreihe ist stets ein Intervall, das symmetrisch zur Entwicklungsstelle liegt. Die Größe dieses Intervalls gibt der Konvergenzradius an. Der Begri Radius kommt dabei aus der Betrachtung von Potenzreihen mit komplexen Zahlen. In der komplexen Ebene konvergieren Potenzreihen innerhalb einer Kreisscheibe. Wir betrachten hier aber nur Potenzreihen mit reellen Zahlen.

Definition 8.6 (Konvergenzradius)

Der Konvergenzradius r > 0 einer Potenzreihe ist eine positive Zahl mit der Eigenschaft, dass die Potenzreihe für alle x mit Sx − x0S < r konvergiert und für alle x mit Sx − x0S > r divergiert. Eine Potenzreihe, die für alle reellen Zahlen x konvergiert, hat einen unendlichen Konvergenzradius r = ∞.

Beispiel 8.7 (Potenzreihe)

Die Potenzreihe p mit Entwicklungsstelle x0 = 0, und Koe zienten ak = 1 für alle k, ist

∞

p(x) = Q xk = 1 + x + x2 + . . . + xn + . . .

k=0

Zwei Fragen müssen wir dabei beantworten. Für welche x-Werte konvergiert die Reihe und können wir p als elementare Funktion darstellen? Die Antwort auf beide Fragen liefert die geometrische Reihe, siehe Beispiel 8.4, denn es ist

Der Konvergenzradius lässt sich aus den Koe zienten der Potenzreihe bestimmen. Die Formeln zur Berechnung des Konvergenzradius leiten sich aus dem Quotientenund dem Wurzelkriterium aus Satz 8.4 ab.

Im schlimmsten Fall ist der Konvergenzradius null. Dann konvergiert die Potenzreihe nur für x = x0. In diesem Fall besteht die Summe nur aus einem einzigen Wert, nämlich aus a0. Ein heikle Frage ist das Konvergenzverhalten am Rande des Konvergenzbereichs. Hat der Konvergenzradius einen endlichen Wert, dann ist oft sehr mühsam zu ermitteln, ob die Reihe für x = x0 ± r konvergiert oder divergiert. Für praktische Problemstellungen ist diese Frage aber in der Regel nicht interessant. Die Konvergenzgeschwindigkeit nimmt mit zunehmender Entfernung von der Entwicklungsstelle ab. Selbst wenn Konvergenz in einem Randpunkt vorliegt, konvergiert die Reihe dort nur sehr langsam.

8.3 Taylor-Reihen

Unser Ziel ist, eine Potenzreihe zu konstruieren, die mit einer gegebenen Funktion f übereinstimmt. Das sogenannte Taylor-Polynom wird aus den Ableitungswerten der Funktion f bis zur Ordnung n an der Entwicklungsstelle x0, also aus f(x0), f′(x0), f′′(x0), . . ., f(n)(x0) gebildet. Die Ableitungen der Potenzreihe

∞

p(x) = Q ak(x − x0)k = a0 + a1(x − x0) + a2(x − x0)2 + . . . + an(x − x0)n + . . .

k=0

an der Stelle x0 sind p(x0) = a0, p′(x0) = a1, p′′(x0) = 2 a2, . . ., p(n)(x0) = n! an. Daraus ergeben sich die Formeln für die Koe zienten der Potenzreihe:

Definition 8.7 (Taylor-Polynom)

Das Polynom Tn vom Grad n, bei dem an der Stelle x0 der Funktionswert und alle Ableitungen bis zur Ordnung n mit einer Funktion f übereinstimmen

nennt man Taylor-Polynom der Ordnung n. Dabei muss die Funktion f in der Umgebung der Entwicklungsstelle x0 mindestens n-mal di erenzierbar sein.

Die Bezeichnung Taylor-Polynom geht auf den englischen Mathematiker Brook Taylor zurück. Die Näherung einer Funktion durch ihr Taylor-Polynom hat gute Approximationseigenschaften in der Nähe des Entwicklungspunktes x0. Die Di erenz zwischen der Funktion f und ihrem Taylor-Polynom Tn hängt im Wesentlichen von der Ordnung n und dem Abstand, den ein Punkt x von der Entwicklungsstelle x0 hat, ab.

Satz 8.6 (Taylor-Restglied)

Die Di erenz zwischen einer Funktion f und dem Taylor-Polynom Tn bezeichnet man als Taylor-Restglied Rn. Das Restglied lässt sich durch

Rn(x) = f(x) − Tn(x) = f(n+1)(ξ)(x − x0)n+1

(n + 1)!

darstellen, dabei ist ξ eine Stelle zwischen x und x0. Die Funktion f muss in der Umgebung der Entwicklungsstelle x0 mindestens (n + 1)-mal di erenzierbar sein.

Das Taylor-Restglied erweckt den Eindruck, dass man die Di erenz zwischen der Funktion f und dem Taylor-Polynom leicht berechnen kann. Leider ist die Sache nicht ganz so einfach. Das Problem ist die Zwischenstelle ξ. Von der Zwischenstelle ξ weiß man nur, dass sie zwischen x und x0 liegt. An allen Stellen x, an denen das Taylor-Restglied für n → ∞ gegen null geht, entsteht beim Grenzübergang aus dem Taylor-Polynom die Taylor-Reihe.

nennt man Taylor-Reihe der Funktion f. Dabei muss die Funktion f in der Umgebung der Entwicklungsstelle x0 beliebig oft di erenzierbar sein. An allen Stellen x, an denen

das Taylor-Restglied den Grenzwert null hat, also lim Rn(x) = 0 gilt, sind Funktion

n→∞

und Taylor-Reihe identisch, also f(x) = T (x).

Auf den ersten Blick vermutet man, dass das Taylor-Restglied genau an allen Stellen x aus dem Konvergenzbereich der Taylor-Reihe gegen null geht. Es gibt jedoch Situationen, in denen die Taylor-Reihe zwar konvergiert, aber der Grenzwert nicht mit dem Funktionswert übereinstimmt. Auf diesen Aspekt gehen wir hier jedoch nicht weiter ein.

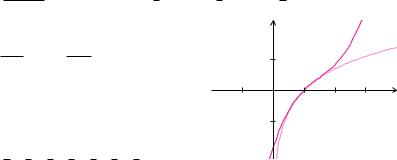
Beispiel 8.8 (Taylor-Reihe des Logarithmus)

An der Stelle x = 0 ist die Funktion f(x) = ln x nicht definiert. Wir bestimmen deshalb die TaylorReihe von f an der Entwicklungsstelle x0 = 1. Dazu benötigen wir die Ableitungsfunktionen

Daraus ergibt sich die Potenzreihe

8.4 Eigenschaften

Es ist prinzipiell möglich, Potenzreihen von Funktionen mithilfe von Taylor-Reihen aus den Werten der Ableitungen an der Entwicklungsstelle herzuleiten. Allerdings ist diese Vorgehensweise ziemlich aufwendig. Es gibt wesentlich elegantere Methoden, mit denen man neue Potenzreihen aus bereits bekannten Potenzreihen herleiten kann. Die Potenzreihen der wichtigsten Funktionen sind in Tabellen festgehalten, siehe Anhang A.3. Methoden, mit denen man aus diesen tabellierten Reihen neue Reihen entwickeln kann, stellen wir in diesem Abschnitt vor. Das folgende Beispiel betrachtet Potenzreihen mit komplexen Zahlen. Wer bisher nicht mit komplexen Zahlen vertraut ist, sollte dieses Beispiel einfach überspringen. Abgesehen von diesem Beispiel werden wir uns bei Potenzreihen ausschließlich auf reelle Zahlen beschränken.

Beispiel 8.9 (Potenzreihen von Sinus und Kosinus)

Potenzreihen lassen sich auch mit komplexen Zahlen definieren. Ohne auf die Details einzugehen, betrachten wir die Potenzreihe der e-Funktion aus Beispiel 8.1, wobei wir x durch i x ersetzen:

Aus der Potenzreihe der e-Funktion ergeben sich die Potenzreihen des Sinus und Kosinus. Beide Reihen konvergieren genau wie die Potenzreihe der e-Funktion für alle reellen Zahlen. Ì

Die Addition und Subtraktion von Potenzreihen ist problemlos möglich, vorausgesetzt, alle Reihen besitzen dieselbe Entwicklungsstelle. Außerdem muss man sich Gedanken über den Konvergenzradius machen.

Satz 8.7 (Addition und Subtraktion von Potenzreihen)

Zwei Potenzreihen mit den Konvergenzradien r1, r2 und derselben Entwicklungsstelle x0 dürfen gliedweise addiert oder subtrahiert werden:

Q ak(x − x0)k ± Q bk(x − x0)k = Q(ak ± bk)(x − x0)k.

Der Konvergenzradius r der neuen Potenzreihe besteht aus dem Minimum der beiden Konvergenzradien der Ausgangsreihen r = min {r1, r2}.

Die Di erenziation und Integration lässt sich bei Potenzreihen, wie auch bei Polynomen, gliedweise durchführen. Darunter versteht man, dass man jedes Glied der Summe einzeln ableiten und integrieren darf. Sowohl Di erenziation und Integration als auch die Bildung einer unendlichen Summe sind Grenzwertprozesse. Letztendlich handelt es sich bei der gliedweisen Vorgehensweise um das Vertauschen von zwei Grenzübergängen. Die mathematische Rechtfertigung für das Vertauschen von Grenzprozessen erfordert einen tieferen Einstieg in die Materie.

Satz 8.8 (Di erenziation und Integration von Potenzreihen)

Jede Potenzreihe ist beliebig oft di erenzierbar und integrierbar. Die Ableitung bzw. die Stammfunktion kann man ermitteln, indem man die Glieder der Reihe einzeln differenziert bzw. integriert. Der Konvergenzradius r bleibt dabei unverändert.

Beispiel 8.10 (Di erenziation und Integration von Potenzreihen)

Aus Beispiel 8.7 kennen wir bereits die Potenzreihe

mit Entwicklungsstelle x0 = 0 und Konvergenzradius r = 1. Für die Ableitung erhalten wir dann

In entsprechender Weise können wir auch die Stammfunktionen betrachten:

Substitution bei Potenzreihen

Mithilfe von Substitutionen kann man aus der Potenzreihendarstellung einer Funktion Potenzreihendarstellungen anderer Funktionen erzeugen. Dabei können die neuen Potenzreihen andere Entwicklungsstellen und andere Konvergenzradien besitzen.

Beispiel 8.11 (Substitution bei Potenzreihen)

a) Wir suchen die Potenzreihe der Funktion

f(x) = x2

9 x2

f hat den Konvergenzradius r = 3.

b)Die Potenzreihe aus Beispiel 8.8

Bei der Multiplikation von Polynomen müssen Klammern ausmultipliziert werden, siehe Satz 5.2. Die Multiplikation von Potenzreihen erfolgt nach demselben Prinzip. Um die Formeln einigermaßen übersichtlich zu gestalten, betrachten wir die Multiplikation und Division nur für Potenzreihen mit der Entwicklungsstelle x0 = 0. Alle Ergebnisse lassen sich auf Potenzreihen mit beliebiger Entwicklungstelle x0 übertragen.

356 8 Potenzreihen

Satz 8.9 (Multiplikation von Potenzreihen)

Die Multiplikation zweier Potenzreihen mit den Konvergenzradien r1 und r2

∞ ∞ ∞

ŒQ ak xk‘ ŒQ bk xk‘ = Q ck xk = a0 b0 + (a0 b1 + a1 b0) x + . . .

ergibt eine Potenzreihe mit Konvergenzradius r = min {r1, r2}. Jeder einzelne Koe zient ck der Produktreihe kann aus dem Cauchy-Produkt ermittelt werden:

k

ck = Qa` bk−` = a0 bk + a1 bk−1 + a2 bk−2 + . . . + ak−1 b1 + ak b0.

`=0

Das Cauchy-Produkt ist nach dem französischen Mathematiker Augustin-Louis Cauchy benannt. Bei der Berechnung des Koe zienten ck mit dem Cauchy-Produkt ergibt die Summe der Indizes immer k. Das ist leicht einzusehen, denn die Produkte mit x müssen zusammen xk ergeben:

a0 x0 bk xk + a1 x1 bk−1 xk−1 + a2 x2 bk−2 xk−2 + . . . + ak−1 xk−1 b1 x1 + ak xk b0 x0.