Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Koch_Mathematik fur das Ingenieurstudium.pdf

Скачиваний:

107

Добавлен:

21.02.2016

Размер:

17.74 Mб

Скачать

☆

<<< < Предыдущая 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146147 / 156147 148 149 150 151 152 153 154 155 156 > Следующая >>>

16.4 Transformation periodischer Funktionen

613

Nachweis des Faltungssatzes verzichten wir. Die Faltung ist ein wichtiges Hilfsmittel zur Lösung von Di erenzialgleichungen mit der Laplace-Transformation, siehe Beispiel 16.16.

16.3.4 Grenzwerte

Bei einigen praktischen Problemstellungen interessiert man sich für das Langzeitverhalten einer Zeitfunktion, siehe Beispiel 16.17. Dieses asymptotische Verhalten gibt beispielsweise bei Lösungen von Di erenzialgleichungen Aufschluss darüber, wie sich ein System im eingeschwungenen Zustand verhält. Mit der Laplace-Transformation kann man diese Information aus der Spektralfunktion ermitteln, ohne den genauen Verlauf der Zeitfunktion zu kennen. Auf einen Nachweis der Grenzwertsätze verzichten wir.

Satz 16.10 (Grenzwertsätze)

Zwischen der Funktion f im Zeitbereich und ihrer Laplace-Transformierten F im Bildbereich bestehen die Zusammenhänge

L t→∞

(

) = s→0 ‰

s F

(

)Ž

t→0

(

) = s→∞ ‰

s F

(

)Ž

lim f

lim

lim f

lim

16.4 Transformation periodischer Funktionen

Das typische Werkzeug für periodische Funktionen sind Fourier-Reihen und die FourierTransformation. Insbesondere im Zusammenhang mit Di erenzialgleichungen betrachtet man jedoch auch die Laplace-Transformation periodischer Funktionen. Genau genommen muss man bei der Laplace-Transformation von einer einseitig periodischen Funktion sprechen. Denn nach wie vor spielen die Funktionswerte für negative Zeiten bei der LaplaceTransformation keine Rolle.

Die komplette Information einer Zeitfunktion f mit Periode T ist in einem endlichen Intervall der Länge T enthalten. Dadurch kann man bei der Laplace-Transformation einer Funktion mit Periode T die Integration auf das Intervall zwischen 0 und T beschränken. Wir verwenden die Formel aus Deﬁnition 16.1 und zerlegen das Integrationsintervall in Einzelintervalle der Länge T :

f(t) c

2 T

3 T

f(t) e−s t dt +

2 T

f(t) e−s t dt + . . .

u t

u t T

u t 2 T

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶

Auf jedes einzelne Integral

wenden wir eine Substitution der Form u

t n T an, wobei

= −

die natürliche Zahl

so gewählt ist, dass alle Integrale auf das

Intervall zwischen 0 und

−

T transformiert werden:

S f(u) e−s u

du	0	T	u		T	)	e−s (u+T )
du	0	f	u		T		e−s (u+T )
	+		(f +
	S	´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
			(	u	)
			(		)

du+S

f(u + 2 T ) e−s (u+2 T ) du+. . .

´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ f(u)

614	16 Laplace-Transformation

Wegen der Periodizität von f können wir für alle natürlichen Zahlen n den Ausdruck f(u + n T ) durch f(u) ersetzen. Außerdem lässt sich der von u unabhängige Faktor e−n T s jeweils vor das Integral ziehen:

’1 e

−

T s

2 T s e

3 T s . . .“

0 T f u e

s u du.

–

−

—

( )

−

–

—

–

² ²

— S

”

•

Die Summe der Vorfaktoren hat die Form einer geometrischen Reihe mit q = e−T s. Somit gilt

f(t) c	s	1		T
			S0	f(u) e−s u du.
		1 − e−T s

Dabei müssen wir natürlich voraussetzen, dass die Reihe konvergiert. Das ist für SqS < 1, also für Re(s) > 0, sichergestellt.

Satz 16.11 (Laplace-Transformation einseitig periodischer Funktionen)

Die Laplace-Transformation einer zumindest einseitig periodischen Funktion f mit der

(

) =

)

kann man durch folgende Formel berechnen:

Eigenschaft

(

f(t) c

f(t) e−s t dt, Re(s) > 0.

1 − e−T s

Beispiel 16.11 (Laplace-Transformation einer periodischen Funktion)

Die Laplace-Transformierte der abgebildeten Funkti-

on f mit Periode T

2 berechnen wir mit der Formel

aus Satz

16.11:

e−s t dt.

)

−

2 s

(

Im Bereich zwischen 0 und 1 gilt f(t) = t, zwischen 1 und 2 hat die Funktion den Wert null. Das Integral

1	f (t)
	f (t)
1	2	3	4	5	6	t
−1

	0 1 t e s t dt			s t e−s 2		e−s t	1		s e−s s2e−s 1
			−	t	−		1	−	− +
S	−	=	−	s	−		Wt=0 =	−	− +

berechnen wir mit einer Stammfunktion, siehe Anhang A.5:

a x e

a x

x e−a x dx =

a2− e

InsgesamtS

erhalten wir

f t

s e−s

e−s

c s

( )

−s2

− e

−

2 s+

(

−

)

16.5 Rücktransformation

615

16.5 Rücktransformation

Die typische Vorgehensweise bei der Laplace-Transformation besteht darin, ein Problem in den Bildbereich zu transformieren und dort zu lösen, siehe Abschnitt 16.6. Allerdings benötigt man dazu die Rücktransformation der Lösungsfunktion vom Bildbereich in den Zeitbereich. Es gibt zwar eine Integralformel, mit der sich die Funktion im Zeitbereich aus der Funktion im Bildbereich berechnen lässt. Diese Art der Rücktransformation erfordert jedoch ein tieferes Verständnis für die Integration in der komplexen Ebene. In der Anwendungspraxis verwendet man Korrespondenztabellen, in denen die wichtigsten Zuordnungen zwischen Zeitfunktionen und Spektralfunktionen enthalten sind, siehe Anhang A.8. Bei vielen Anwendungen treten im Bildbereich gebrochenrationale Funktionen auf. Bei Nennerund Zählerpolynomen von höherem Grad sind diese Funktionen nicht tabelliert. Sie lassen sich jedoch durch Partialbruchzerlegung in eine Summe aus einfacheren Brüchen zerlegen, siehe Abschnitt 5.2.3, und dann aufgrund der Linearität zurücktransformieren. Ein weiteres wichtiges Hilfsmittel zur Rücktransformation ist die Faltung, siehe

Satz 16.9.

Rücktransformation vom Bildbereich in den Zeitbereich

Die wichtigsten Hilfsmittel zur Rücktransformation einer Funktion aus dem Bildbereich in den Zeitbereich sind bei der Laplace-Transformation

LKorrespondenztabellen,

LPartialbruchzerlegung und

LFaltung.

Beispiel 16.12 (Rücktransformation durch Partialbruchzerlegung)

Wir suchen eine Zeitfunktion f, sodass die Laplace-Transformation von f die Spektralfunktion

F (s) =

s3 − 4 s2 + 5 s − 2

ergibt. Der erste Schritt bei der Partialbruchzerlegung ist die Bestimmung aller Nennernullstellen, siehe Abschnitt 5.2.3.

(1) Die Nullstelle s1 = 1 kann man beispielsweise durch Raten ﬁnden:

s3 − 4 s2 + 5 s − 2 = 0 Ô 13 − 4 12 + 5 1 − 2 = 0 Ô s1 = 1.

Die weiteren Nullstellen ﬁndet man durch Polynomdivision

‰s3 − 4s2 + 5s − 2 Ž ‰s − 1Ž = s2 − 3s + 2

−s3 + s2

−3s2 + 5s

3s2 − 3s

2s − 2

− 2s + 2

616	16 Laplace-Transformation

und durch Lösen der quadratischen Gleichung

√

s2 − 3 s + 2 = 0 Ô s2,3 = 3 ± 9 − 8 = 1, 2. 2

(2)Bei s1,2 = 1 handelt es sich um eine doppelte Nullstelle, s3 = 2 ist eine einfache Nullstelle. Deshalb verwenden wir den Ansatz

			A	2		B	1			C			A	s	−	1	)	2	+	B	(	s	−	1 s			2		) +	C s	2	)
				2			1			1			(		−		)		+		(		−	)( −					) +	( −		)
F	s																																.
	(	) =	−		+	−		+ (	s	− )	2	=								( −			)( −		1	)		2
		s			s				s		2									s			2	s	1			2

(3) Durch Ausmultiplizieren des Zählers erhalten wir

s = A s2 − 2 A s + A + B s2 − 3 B s + 2 B + C s − 2 C.

Ein Koe zientenvergleich ergibt das lineare Gleichungssystem

2 A

3 B

−A

−

2 B

2 C

mit der

−

2, B

2 und

C 1. Die Korrespondenzen aus Bei-

eindeutigen Lösung A

spiel 16.1 zusammen mit einer

Zeitverschiebung, siehe Satz 16.3, ergeben die Rücktransfor-

= −

mation:

−

( )

−

(

−

)

c s

f t

2 e2 t

2 et

t et

−

( )

16.6 Lösung gewöhnlicher Di erenzialgleichungen

Bei praktischen Problemen wird die Laplace-Transformation hauptsächlich zur Lösung von Di erenzialgleichungen eingesetzt. Wir betrachten in diesem Abschnitt lineare Di e- renzialgleichungen mit konstanten Koe zienten, siehe Deﬁnition 12.16 und lineare Differenzialgleichungssysteme mit konstanten Koe zienten, siehe Deﬁnition 12.30. Für das Verständnis der in diesem Abschnitt präsentierten Methoden ist ein Grundverständnis für Di erenzialgleichungen erforderlich. Die Lösungsmethoden unterscheiden sich jedoch grundsätzlich von den Verfahren aus Kapitel 12.

Die wesentliche Idee besteht darin, die Di erenzialgleichung in den Bildbereich zu transformieren und dort zu lösen. Durch die Transformation einer linearen Di erenzialgleichung oder eines linearen Di erenzialgleichungssystems mit konstanten Koe zienten in den Bildbereich ergibt sich eine algebraische Gleichung. Gelingt es, diese algebraische Gleichung zu lösen, dann kann man die Lösung im Zeitbereich durch Rücktransformation der Lösung im Bildbereich berechnen.

x(t)

16.6 Lösung gewöhnlicher Di erenzialgleichungen

617

Lösung einer Di erenzialgleichung mit der Laplace-Transformation

Folgende Schritte führen auf eine Lösung:

(1)Transformiere die Di erenzialgleichung in den Bildbereich.

(2)Berechne die Lösung der algebraischen Gleichung im Bildbereich.

(3)Transformiere die Lösung der algebraischen Gleichung zurück in den Zeitbereich.

Di erenzial-	c	s	Algebraische
gleichung	c	s	Gleichung
×			×
×	c	s	×
Ö	c	s	Ö
Lösung			Lösung ×
×			Lösung ×
Zeitbereich			Bildbereich
Zeitbereich			Bildbereich

Bei der Laplace-Transformation der Di erenzialgleichung arbeitet man mit Platzhalter für die zu berechnende Lösungsfunktion. Wenn x die gesuchte Lösung der Di erenzialgleichung ist, dann verwendet man die Korrespondenz

c s X(s) Ô x c s X.

Dabei ist es üblich, sowohl im Zeitbereich als auch im Bildbereich auf die explizite Angabe der Variablen t und s zu verzichten.

Das Hauptproblem bei der Lösung von Di erenzialgleichungen mit der Laplace-Transfor- mation liegt typischerweise in der Rücktransformation der Lösung aus dem Bildbereich in den Zeitbereich. Dabei sind unterschiedliche Strategien erforderlich, siehe Abschnitt 16.5.

Beispiel 16.13 (Anfangswertproblem mit Di erenzialgleichung erster Ordnung)

Zur Lösung des Anfangswertproblems transformieren wir die Di erenzialgleichung unter Berücksichtigung des Anfangswerts in den Bildbereich:

−

4 t, x 0

) =

+ 2

(

s X 1

2 X

Bei der Transformation− +

=dersAbleitung−

haben wir Satz 16.5 zur Di erenziation im Zeitbereich

verwendet. Die restlichen Korrespondenzen ergeben sich aus der Tabelle im Anhang A.8. Die Gleichung im Bildbereich lässt sich problemlos nach unserer gesuchten Spektralfunktion X auflösen:

s X + 2 X = 1

−

X =

−

s 2

s s 2

s2 s 2

Die Rücktransformation erfolgt mithilfe der

Korrespondenztabelle aus Anhang A.8:

(

)

( + )

−

s 2

)

(

)

2 t

2 e−2 t

4 e−2 t

2 t

−

2−

−

2 t

( ) =

−

2 t

Die Lösung des

Anfangswertproblems ist x t

−

618	16 Laplace-Transformation

Vorteile der Laplace-Transformation

Die Lösung einer linearen Di erenzialgleichung mit der Laplace-Transformation bietet folgende Vorteile:

LAnfangswerte werden bei der Transformation in den Bildbereich berücksichtigt.

LEine separate Betrachtung der homogenen und der inhomogenen Di erenzialgleichung ist nicht erforderlich.

Beispiel 16.14 (Randwertproblem mit Di erenzialgleichung zweiter Ordnung)

Wir betrachten das Randwertproblem

x¨ 9 x 0, x

π2

1, x π

Zur Transformation+ =

der‰

DiŽ =erenzialgleichung( ) = −

benötigen wir Anfangswerte zum Zeitpunkt t

Da wir diese Werte nicht kennen, arbeiten wir mit Parametern:

x 0

C ,

x˙ 0

C2.

Damit ergibt( ) =die1Transformation( ) =

in den Bildbereich

x¨

9 x

s2 X s C1 C2

9 X

Die Lösung

der Gleichung im Bildbereich ergibt

−

C1 s

X +

9 X

= C2 + C1 s

Ô X

s2 9

Aus der Korrespondenztabelle im Anhang A.8

bestimmen wir die Rücktransformation:

s + 9

cos (3 t)

+ C1 sin (3 t)

Somit haben wir die allgemeine Lösung der Di erenzialgleichung

x(t) =

cos (3 t) + C1 sin (3 t)

bestimmt. Die Lösung des Randwertproblems ergibt sich aus den Randwerten:

x ‰ 2

Ž = 1

Ô −C1 = 1,

x(π) = −1

Ô −

= −1.

Die Lösung des Randwertproblems lautet x(t) = cos (3 t) − sin (3 t).

16.6 Lösung gewöhnlicher Di erenzialgleichungen

619

Allgemeine Lösung einer Di erenzialgleichung mit Laplace-Transformation

Zur Bestimmung der allgemeinen Lösung einer linearen Di erenzialgleichung mit der Laplace-Transformation kann man für die Anfangswerte zum Zeitpunkt t = 0 Parameter einführen:

x(0) = C1, x˙(0) = C2, x¨(0) = C3, . . .

Dadurch kann man auch Anfangswertprobleme, bei denen die Anfangswerte nicht zum Zeitpunkt t = 0 gegeben sind, und Randwertprobleme lösen.

Beispiel 16.15 (Di erenzialgleichung zweiter Ordnung mit Resonanz)

Zur Lösung des Anfangswertproblems

x¨

−

3 x˙

2 x

et, x

(

) =

0, x˙ 0

( ) =

transformieren wir die Di erenzialgleichung mit den Anfangswerten in den Bildbereich:

x¨

−

3 x˙

2 x

s2 X − 1 − 3 s X + 2 X =

s 1

Die Lösung der Gleichung im

Bildbereich ergibt

−

s2 X

s X

−

+ 2

= 1

+ s

−

Ô2 t

−

)(

−

3 s

2 e

( ,

)

Die Rücktransformation ergibt x t

) =

−

t e

siehe Beispiel 16.12.

(

Bei der Di erenzialgleichung in Beispiel 16.15 liegt Resonanz vor, siehe Abschnitt 12.3.4. Bei der Lösung des Problems mit der Laplace-Transformation wird dieser Aspekt quasi automatisch berücksichtigt.

Laplace-Transformation bei Di erenzialgleichung mit Resonanz

Die Laplace-Transformation kann auch im Resonanzfall zur Lösung einer linearen Differenzialgleichung mit konstanten Koe zienten verwendet werden.

In Beispiel 16.15 taucht bei der Lösung des Problems das charakteristische Polynom, siehe Deﬁnition 12.17, auf. Das ist kein Zufall. Transformiert man eine lineare homogene Di erenzialgleichung mit konstanten Koe zienten mit Nullanfangsbedingungen

	x	(	0	) =	0,	x˙	0	) =	0,	x¨	(	0	) =	0, . . .
in den		(		) =		(		) =			(		) =
	Bildbereich

an x(n) + an−1 x(n−1) + . . . + a2 x¨ + a1 x˙ + a0 x = 0

an sn X + an−1 sn−1 X + . . . + a2 s2 X + a1 s X + a0 X = 0

620	16 Laplace-Transformation

dann entsteht die charakteristische Gleichung mit der Variablen s anstelle von λ. Das homogene Problem mit Nullanfangsbedingungen hat natürlich die triviale Lösung. Wenn die Di erenzialgleichung jedoch inhomogen oder eine Anfangsbedingung ungleich null ist, dann taucht das charakteristische Polynom im Nenner auf.

Beispiel 16.16 (Anfangswertproblem mit Rechteckfunktion als Störfunktion)

Beim Anfangswertproblem

x¨ + 4 x = r(t), x(0) = 0, x˙(0) = 0

ist die Störfunktion eine Rechteckfunktion

r(t) = œ	1	für	0	≤	t	≤	1
r(t) = œ	0	sonst .		≤		≤

1	r(t)
1
	1	t

Wir transformieren die Di erenzialgleichung in den Bildbereich:

x¨ + 4 x = r(t)

s2 X + 4 X = R(s)

Für die Laplace-Transformation der Rechteckfunktion r verwenden wir den Platzhalter R. Wir werden das Problem lösen, ohne R explizit zu bestimmen. Die Lösung der Gleichung im Bildbereich ergibt

2		1
s	X + 4 X = R(s) Ô	X =		R(s).
			s2 + 4

Nach dem Faltungssatz im Zeitbereich, siehe Satz 16.9, können wir die Lösung x durch eine Faltung berechnen:

1 sin

2 t

2 τ

dτ.

R s

x t

r t

sin

r t

2 s2

) †

( ) =

(

)

(

−

)

Falls

t kleiner als 1 ist, verläuft der Integrationsbe-

( ) =

( )

( ) =

(

S r(t

−

τ )

reich zwischen 0 und t:

x t

sin

2 τ

dτ

cos

2 sin (2 τ)

( ) =

( )

‰ − ( )ŽT

t −1

‰1 − cos (2 t)Ž.

Wenn t größer als 1 ist, dann startet der Integrationsbereich bei t − 1 und endet bei t:

	1	t	1			t
x(t) =		St−1sin (2 τ) dτ =			‰−cos (2	τ)ŽTt−1
	2			4

=1 ‰ cos (2 t − 2) − cos (2 t)Ž . 4

1		r(t − τ )
		1 sin (2 τ)
		2
t −1	1	t	τ
t −1	1	t

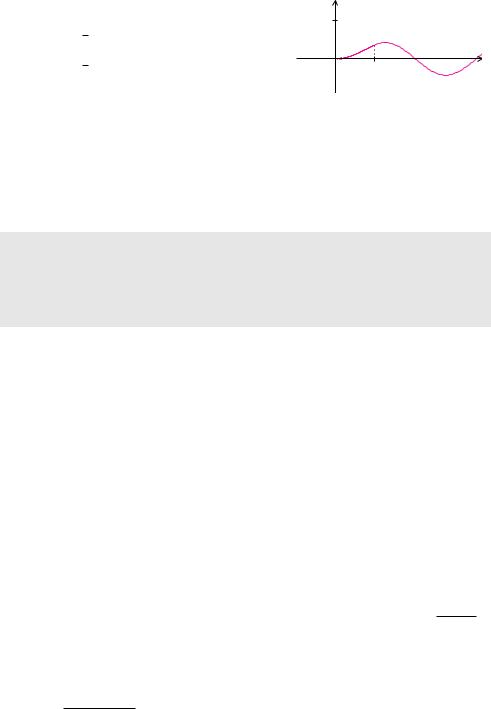
16.6 Lösung gewöhnlicher Di erenzialgleichungen

621

Insgesamt besteht die Lösung aus zwei Abschnitten:

x t

cos

für 0

x(t)

−

(

)Ž

≤

‰

t .

( ) = ¦

cos

für 1

‰

(

−

) −

(

)Ž

Die Di erenzialgleichung aus Beispiel 16.16 ist mit klassischen Hilfsmitteln nur schwer in den Gri zu bekommen. Für die abschnittsweise deﬁnierte Störfunktion, die sogar eine Sprungstelle besitzt, fehlt uns bei der klassischen Lösungstheorie ein geeigneter Ansatz zur Bestimmung einer partikulären Lösung, siehe Abschnitt 12.3.4. Mithilfe der LaplaceTransformation können wir elegant Probleme lösen, die mit den klassischen Methoden aus Kapitel 12 nur schwer zu bewältigen sind.

Lineare Di erenzialgleichungen mit abschnittsweise deﬁnierten Störfunktionen

Die Laplace-Transformation kann man auch zur Lösung linearer Di erenzialgleichungen verwenden, bei denen die Störfunktion eine abschnittsweise deﬁnierte Funktion ist und sogar Sprungstellen haben darf. Zur Rücktransformation verwendet man dabei in der Regel den Faltungssatz.

Beispiel 16.17 (Di erenzialgleichungssystem)

Wir betrachten ein Anfangswertproblem, das aus einem linearen Di erenzialgleichungssystem zweiter Ordnung und vier Anfangswerten zum Zeitpunkt t = 0 besteht:

x¨

2 y¨

x˙

−

2 y

4 σ t , x 0

x˙ 0

x¨

y˙

σ(t), y(0) =

y˙

(0) =

−

( )

( ) =

Die Transformation der Gleichungen in den Bildbereich ergibt:

s2 X

−

2 s2

−

) +

s X

2 Y

(

−

s X − 3

s Y − X

Dabei bezeichnen X und Y die Transformationen unserer gesuchten Funktionen x und y. Im Bildbereich erhalten wir das lineare Gleichungssystem mit Parameter s, das sich durch Division

mit dem Faktor

vereinfachen lässt:

s + 1

5 s

4 5 s

)

(

−

)

s X

(

−

)

s s+

(

1 + 3 s

1 3 s

(

−

)

−

)

( +

)

s s

+ ( +

(

)

Die Lösung dieses Gleichungssystems lautet

( +

6 s

2 s2

, Y

−

)

2 s2

−

(

<<< < Предыдущая 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146147 / 156147 148 149 150 151 152 153 154 155 156 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.11.2018280.06 Кб6group_sex.docx
#
24.11.201935.46 Кб5hgfgk,jgggk,j.docx
#
21.02.201667.9 Кб12Istoriya_ukr_kult_mk2.docx
#
21.02.20161.56 Mб37KaossPad3_Reference_Manual_Ru.pdf
#
21.02.2016296.36 Кб6KLISHENKO.pdf
#
21.02.201617.74 Mб107Koch_Mathematik fur das Ingenieurstudium.pdf
#
21.02.20162.04 Mб7Konspekt_teplofizika.doc
#
21.02.2016611.84 Кб20KR-nadijnist-el-meh-system.doc
#
20.08.2019517.12 Кб1KURSOVA_VARIANT2.doc
#
21.02.20162.57 Mб15Kursovoy_stroy_konstruktsii.docx
#
21.02.20162.35 Mб25KURS_P_EO-METODICA.doc