ВСТУП

Значення обчислювальних машин і головним чином електронних обчислювальних машин в справі технічного прогресу нашої країни виключно велике. Сучасні електронні цифрові обчислювальні машини проводять десятки тисяч арифметичних і логічних операцій в секунду і здатні у виключно короткі терміни давати рішення складних математичних і технічних задач, немислимі при ручному розрахунку.

Величезна швидкодія обчислювальних машин відкриває нові широкі можливості для застосування загальних математичних методів дослідження в проблемах теплофізики і багатьох інших областей.

Принципова відмінність від колишнього стану речей полягає в тому, що складні технічні питання можуть розв'язуватися в точній постановці, недоступній для малих обчислювальних машин через надмірний обсяг роботи.

Виняткове значення мають електронні машини для автоматичного управління швидко рухомими об'єктами, наприклад міжпланетними ракетними снарядами. Велика також роль електронних обчислювальних машин для розвитку самої математики. Машини використовуються для підрахунку математичних постійних; для вирішень, трансцендентної і диференціальної рівнянь, алгебри; для вирішення складних функціональних нерівностей і т.п. З'явилися нові статистичні методи машинного рішення задач математичної фізики, стало можливим експериментальне рішення логічних задач і багато що інше.

Таким чином, створення електронних обчислювальних машин знаменує рішучий стрибок по шляху прогресу точних і технічних наук нашого часу.

Все це зробило вельми актуальним удосконалення і розвиток чисельних і наближених методів рішення задач. Річ у тому, що машина здатна виконувати дуже велике, але кінцеве число операцій. Тому точні граничні процеси рішення задач, пов'язані з нескінченним числом операцій, при роботі на машині з потреби повинні бути замінені наближеними алгоритмами, що містять лише кінцеве число дій. Наприклад, при машинному обчисленні певного інтеграла останній звичайно замінюється кінцевою інтегральною сумою, замість диференціального рівняння розглядається кінцева система рівнянь в кінцевих різницях і т.п. Крім того, машина володіє кінцевою пам'яттю і може оперувати з числами лише кінцевої довжини. Тому проміжні результати округляються, внаслідок чого навіть точний метод з кінцевим числом дій стає наближеним.

В даний час розробка чисельних і наближених методів рішення задач в основному протікає в двох напрямах: з одного боку, створюються ефективніші детерміновані способи рішення задач, що враховують специфічні особливості рахункових машин; з іншого боку, в практику успішно упроваджуються статистичні недетерміновані методи, засновані на випадкових випробуваннях (метод Монте-Карло та інші).

Висока продуктивність електронних машин істотним чином змінила підхід до оцінки того або іншого обчислювального методу. Цінним виявляється той метод, який є найбільш універсальним і який допускає просту реалізацію на машинах. Навпаки, метод, заснований на приватних особливостях завдання або на здатності обчислювача, виявляється тепер мало придатним. У зв'язку з цим відбулася своєрідна переоцінка цінностей: багато обчислювальних методів, що приводили до громіздкого рахунку і вважалися раніше, при ручному рахунку, непрактичними, виявилися зараз цілком робочими. В той же час чисто аналітичні конструкції, що ведуть до незручних обчислювальних алгоритмів, втратили свою минулу цінність. От чому зараз великого поширення набули ітеративні, різницеві, варіаційні, імовірнісні і т.п. методи рішення задач, допускаючі зручні схеми рахунки і застосовні до широкого круга проблем.

При наближеному рішенні задач необхідна оцінка погрішності отриманого результату. Тут при обчисленнях з великим числом кроків ми стикаємося з новою вельми важливою проблемою — питанням стійкості обчислювальної схеми. Може трапитися, що неминучі погрішності округлень швидко накопичуються (наприклад, мають показове зростання). Така обчислювальна схема нестійка і непридатна для практики. Допустимо користуватися лише стійкими обчислювальними схемами, коли погрішності округлень взаємно компенсуються і помилка результату, що викликається ними, залишається малою для всього процесу обчислень.

Для вивчення реального фізичного об'єкту сучасним є наступний підхід (схема ОЕ).

1. фізична модель

2. математична модель

3. дискретна модель та алгоритми

4. програма (ПП)

5. розрахунки на ЕОМ

Математична модель – замкнена система рівнянь, яка описує найбільш суттєві риси і властивості об'єкту, що вивчається.

Таким чином, математична модель заснована на певному спрощенні, ідеалізації не тотожна об'єкту, а є його приблизним описом.

Реальному об'єктові може слідувати декілька математичних моделей. Чим точніше результати, тим складніше, зазвичай, математична модель.

Описавши поведінку об'єкта, що вивчається, математичною мовою ми можемо скористатися універсальним математичним апаратом, який не залежить від природи об'єкту. Це дозволяє:

• одноманітно описати широке коло фактів і спостережень

• провести їх детальний кількісний аналіз

• передбачити, як поведе себе об'єкт в різних умовах, тобто спрогнозувати результати майбутніх спостережень.

Прогнозування – завжди важка задача, і виправдані прогнози є предметом особливої гордості людей науки.

Здатність побудови і використання математичної моделі суттєво залежить від здатності об'єкта, що вивчається.

В математиці часто зустрічаються задачі, рішення яких не вдається отримати в вигляді формули, що пов'язує шукану величину з заданими. Про такі задачі кажуть, що вони не вирішуються в явному вигляді. Для їх вирішення прагнуть знайти певний нескінчений процес, що сходиться до шуканої відповіді. Якщо такий процес вказаний, то виконується певна кількість кроків, і потім обриваючи обчислення (їх не можна продовжувати нескінченно), ми отримаємо наближене рішення задачі. Така процедура, пов'язана з проведенням обчислень за строго визначеною системою правил, яка завдається характером процесу має назву алгоритм.

Такий підхід до рішення задач був відомий ще до появи ЕОМ, проте використовувався досить рідко через виключну трудомісткість великих обчислювань. В більшості випадків дослідники намагались уникнути великих обчислень, тому складні математичні моделі, для яких не вдавалось отримати відповідь у вигляді формули, або взагалі не роздивлялися, або спрощувались за допомогою додаткових припущень. Спрощення моделі знижувало ступінь відповідності дослідному об'єктові, робило результати досліджень об'єкта менш точними, і, таким чином, менш інженерними ,а інколи й взагалі помилковими.

Досвідчений обчислювач витрачав на виконання однієї арифметичної дії в середньому за робочу зміну близько півхвилини, в той час, як сучасні ЕОМ виконують близько 10¹⁴ операцій в секунду.

Використання чисельних методів на базі ЕОМ відразу суттєво розширило клас математичних задач, що допускають суттєвий аналіз. Тепер вже досліднику (інженеру) для побудування математичної моделі певного об'єкта немає потреби прагнути сильних спрощень (для отримання відповіді у явному вигляді). Його увага, насамперед, повинна бути звернена на те, щоб вірно врахувати всі найбільш суттєві особливості об'єкта, що вивчається, і відобразити їх в математичній моделі.

Після побудування моделі стає питання щодо розробки алгоритму рішення відповідної математичної задачі і про його реалізацію на ЕОМ. Таким чином, ЕОМ змінило підхід до використання математики як методу досліджень.

В наш час ЕОМ є одним з визначальних факторів НТП, адже вони відкрили принципово нові можливості проектування складних систем ,вибору оптимальних прикладів роботи об'єктів.

Очевидно, що всі колись зіштовхувались з задачами, в яких було конкретно вказано, що дане (нехай дане…) і потім на мові строго визначених математичних понять слідує повне викладення вихідних передумов ,які сприймаються однаково будь-яким математиком, що є спеціалістом в відповідній області.

Інколи справа стосується прикладних задач. В них безпосередньо завдається реальний нематематичний об'єкт: система керування, економічний план і так далі. Дослідження починається з формалізації об'єкта, з побудови відповідної математичної моделі: виділяються його най суттєві риси і властивості і описуються за допомогою математичних співвідношень. Тільки після того, як побудована математична модель, тобто задачі надана математична форма ,можна користуватися для її вивчення математичними методами.

Математичні моделі є досить поширеними ,хоча людина, що має з ними справу, можливо й не зустрічала цього терміну. Уявімо собі, що потрібно визначити площу поверхні письмового столу. Для цього вимірюють його довжину й ширину ,а потім перемножують отримані числа. Така елементарна процедура фактично означає наступне: реальний об'єкт – поверхня столу – замінюється абсолютною математичною моделлю – прямокутником. Прямокутнику приписуються розміри ,що отримані внаслідок вимірювань, і площа такого прямокутника наближено приймається за шукану площу.

Заміняючи поверхню стола прямокутником ми спираємося на своє зорове сприйняття. При більш серйозному підході перед тим ,як скористатися моделлю прямокутника, її необхідно перевірити: виміряти довжину протилежних сторін столу, його діагоналей і порівняти вимірювання. Якщо з ступенем точності, що вимагається, довжини протилежних сторін і довжини діагоналей попарно рівні, то поверхню столу дійсно можна розглядати як прямокутник. В зворотному випадку модель прямокутника прийдеться замінити на модель чотирикутника загального вигляду. При більш високій вимозі точності може виникнути необхідність в ще більшому уточненні моделі ,наприклад, врахувати закруглення кутів столу.

Таким чином математична модель не визначається однозначно дослідним об'єктом. Для столу:

• модель прямокутника,

• модель чотирикутника загального вигляду,

• модель чотирикутника загального вигляду з закругленими кутами.

Вибір моделі визначається вимогою точності. З підвищенням точності модель потрібно ускладнювати, враховуючи все нові особливості об'єкта, що вивчається.

Роздивимось в якості прикладу наступну задачу з механіки: тілу на Землі надали початкову швидкість , що направлена під кутом α до ї поверхні. Потрібно знайти траєкторію руху тіла і підрахувати відстань між її початковою і кінцевою точками.

Щоб зробити задачу більш конкретною вважатимемо, що мова іде про камінь, що кинутий за допомогою катапульти. Це дає характерні розміри тіла, його масу і можливу початкову швидкість.

Побудуємо математичну модель, що заснована на припущеннях:

1. Земля – інерційна система підрахунку (тобто нехтується обертання Землі навколо власної осі і навколо Сонця);

2. прискорення вільного падіння g стале;

3. кривизною Землі можна знехтувати і вважати її пласкою;

4. дією повітря на рух каменю, що рухається, можна знехтувати.

За умови зроблених припущень проекція каменя на вісьх буде рухатися рівномірно зі швидкістю .

Рух проекції каменя на вісь y рівноприскорений з прискоренням і початковою швидкістю.

Таким чином, рух каменя визначається формулами

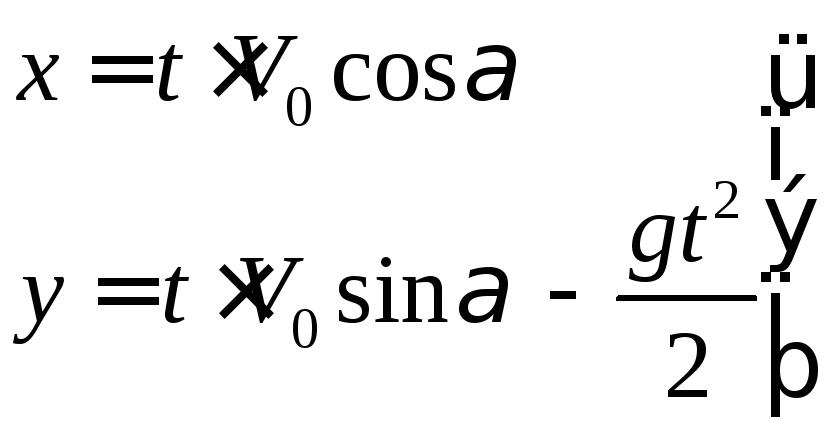математична модель задачі в припущеннях 1-4.

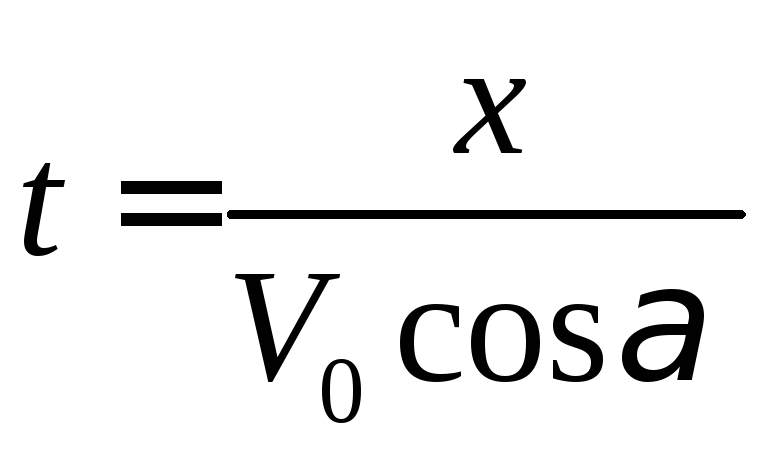
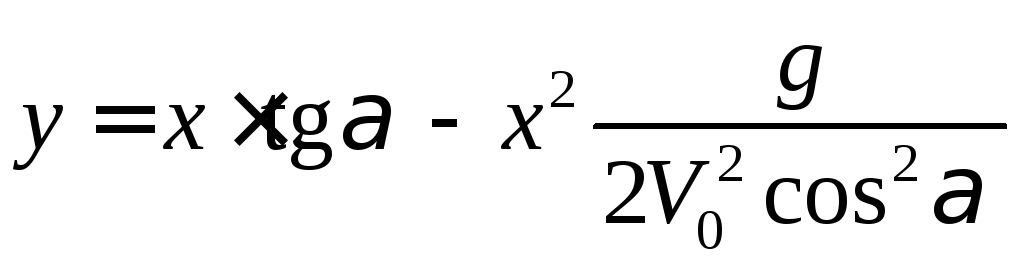–парабола.

Отримана модель є досить простою і з її допомогою можна легко відповісти на поставлену задачу

(*)

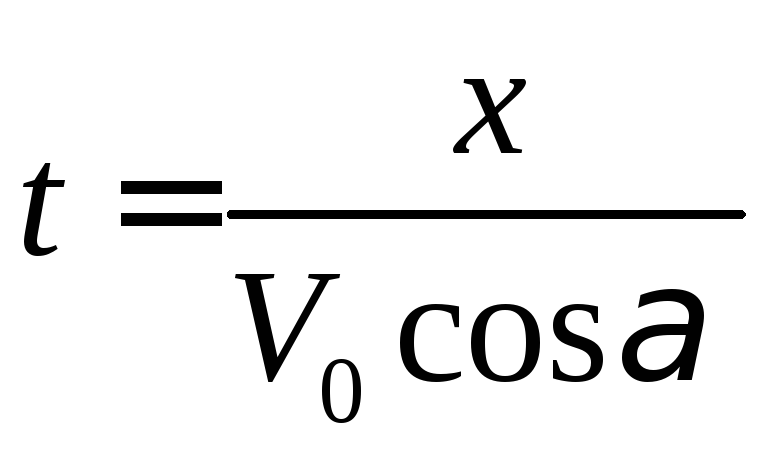
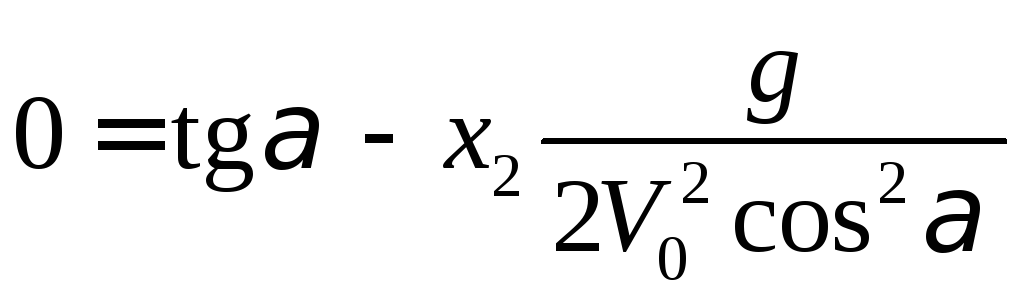
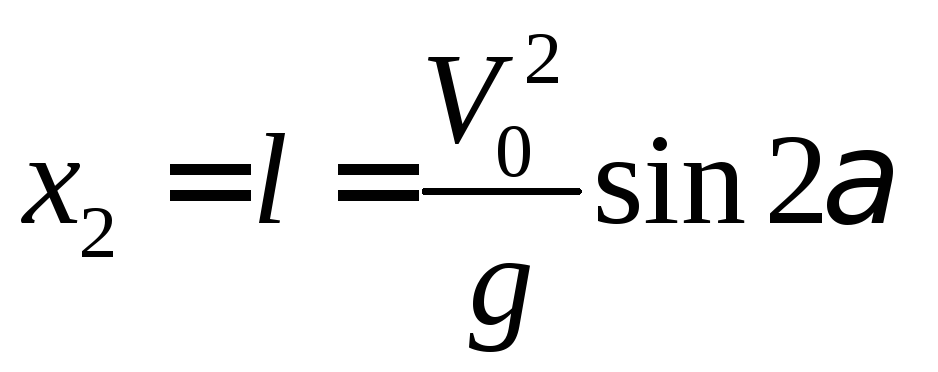В прикладних задачах побудування математичної моделі – це один з найбільш складних і відповідальних етапів роботи. Дослід показує, що вірно вибрати модель – вирішити проблему більш ніж наполовину. Важкість даного етапу полягає в тому, що він вимагає поєднання математичних і спеціальних знань.

Відповідність математичної моделі об'єктові, що вивчається. Критерій практики.

Математична модель ніколи не буває тотожна об'єктові, що розглядається. Заснована на спрощенні, ідеалізації вона є наближеним описом об'єкта. Тому результати, які отримані при аналізі моделі, завжди носять для об'єкту наближений характер. Їх точність визначається ступенем відповідності, адекватності моделі та об'єкту. Питання про точність – одне з найтонших питань.

Найбільш просто це питання вирішується, коли добре відомі закони ,що визначають поведінку об'єкту, і є досить великий практичний досвід їх застосування. Тоді можна заздалегідь (до досліду, тут – до початку рішення математичної задачі) оцінити точність результатів.

Наприклад, розрахунок траєкторії штучного супутника Землі в міжпланетному просторі проводиться на основі математичної моделі, що використовує закони механіки та закон всесвітнього тяжіння. Універсальність законів природи слугувала гарантією застосування моделі. Більш складна ситуація виникає тоді, коли знання щодо об'єкту, який вивчається, не достатні. В цьому випадку доводиться робити додаткові припущення, які носять характер гіпотез. Висновки, отримані на основі цієї гіпотетичної моделі, носять умовний характер. Для їх перевірки необхідно зіставити результати моделі з усією інформацією, що існує щодо об'єкту, який вивчається. Основним критерієм істинності є експеримент, практика в найширшому змісті цього слова. Критерій практики дозволяє обрати з усіх математичних моделей ту, яка є найбільш простою і в той самий час у рамках потрібної точності вірно передає властивості об'єкту, що вивчається.

Для зображення цих відповідностей повернемося до нашого прикладу про траєкторію каменя. Математична модель була побудована на основі чотирьох спрощуючих пропозицій і була отримана формула (*) для дальності кидку.

Оцінимо точність цієї формули. Для цього немає потреби самостійно проводити експерименти з катапультою, адже можна скористатися вже накопиченим експериментальним та теоретичним матеріалом. Потрібно лише вміти їм скористатися.

Продивимося ще раз спрощуючі припущення і проаналізуємо їх.

Нехай , α = 45º

h = 20·30 м; t = 5 c.

В цих умовах найбільш уразливим здається четверте припущення щодо впливу повітря. Проаналізуємо його. На всіляке тіло, що рухається в повітрі, воно діє з певною силою . Її модуль і напрямок залежать від форми поля і швидкості руху. Силуможна розкласти на дві складові: паралельно і перпендикулярно швидкості руху.

Перпендикулярна складова виникає тільки при наявності асиметрії тіла по відношенню до напрямку руху. Наприклад, підйомна сила, що діє на крило літака. Проте для каменя, форма якого близька до сфери перпендикулярна складова мала і нею можна знехтувати (для кулі дорівнює нулеві)|підіймальна|.

Паралельна складова виникає завжди, вона направлена в бік, протилежний руху і намагається загальмувати тіло, її називаютьлобовим опором.

Таким чином, в нашому випадку . Модуль лобового опоруможна представити у вигляді

С є функцією від Re та форми тіла.

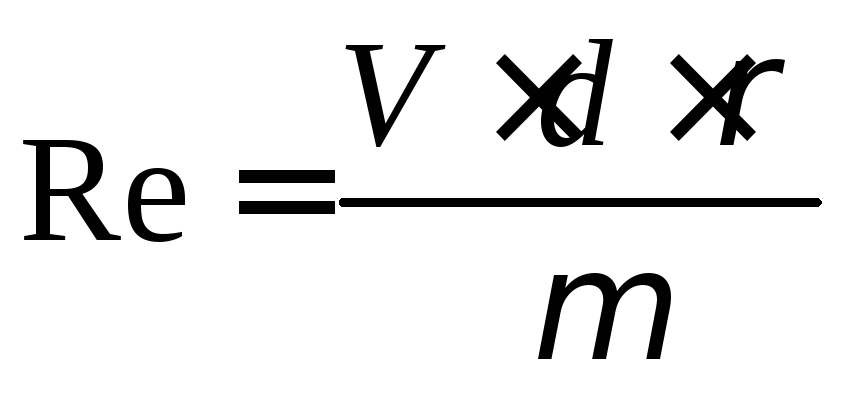
Для d = 0,2 м, V = 30 м/c, ρ = 1,2 кг/м³, μ = 1,7·10^-5 Па·с

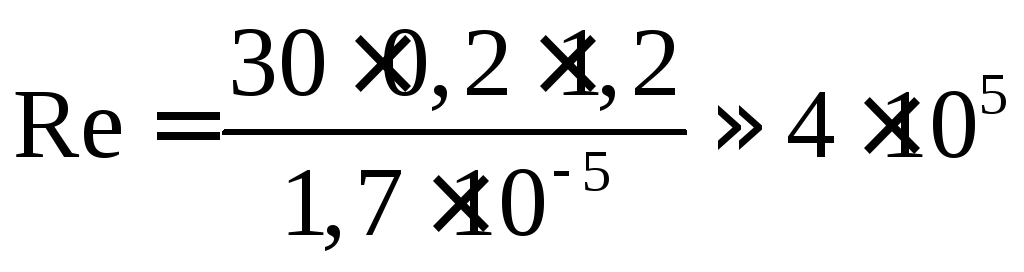
Для для кулі

.

Для оцінки впливу опору повітря на характер руху порівняємо його з основною силою – силою тяжіння .

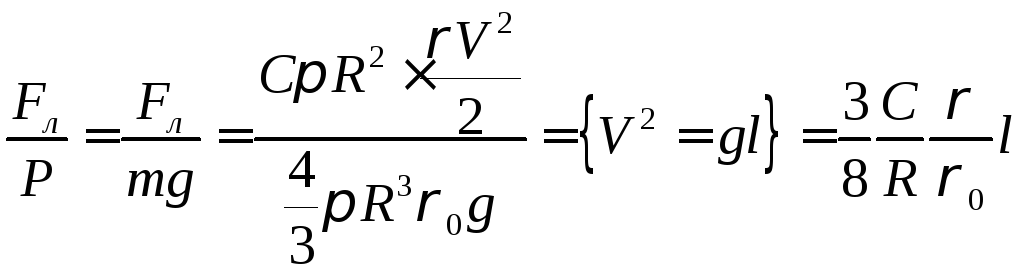
Для каменя

(**)

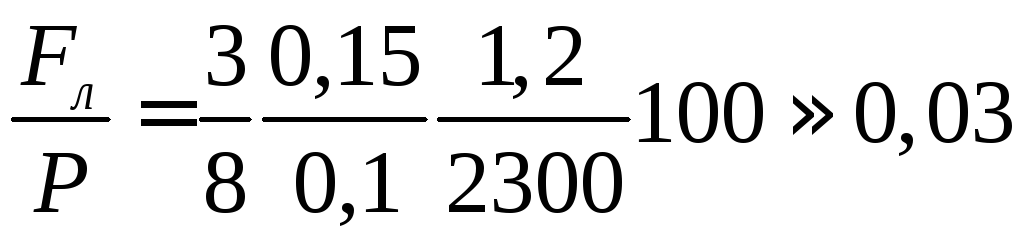Таким чином, опір повітря дає помилку приблизно 3 % при малому опорі

тобто та.

Даний аналіз дозволив встановити для математичної моделі умови застосовності пов'язуючи їх з цілим діапазоном зміни основних параметрів і точності, що вимагається.

Уточнення математичної моделі.

Проведемо аналіз математичної моделі для чавунного ядра вважаючи l = 1 км, R = 0,07 м, ,с = 0,15.

(15 %) (~150 м).

Якщо розглядати математичну модель чавунного ядра, яка враховує опір повітря, то при незмінних трьох перших припущеннях, четверте пере формулюється:

4) повітря діє на ядро при його русі з силою , її модуль визначається за формулою (), а напрямок протилежний напрямку швидкості.

Урахування опору повітря суттєво ускладнюють задачу. Тепер вона вже не допускає рішення у вигляді простих аналітичних формул і може бути вирішена лише за допомогою чисельних методів.

По мірі підвищення вимог точності можливий перегляд і всіх інших припущень.

Структура похибки.

Існують чотири джерела похибки результату: математична модель, вихідні дані, наближений метод та округлення при розрахунках.

Похибка математичної моделі пов'язана з фізичними допущеннями.

Похибка вихідних даних пов'язана з тим, що вихідні дані відомі, зазвичай, наближені (наприклад, з експерименту). У більшості фізичних експериментах точність доходить до 10¹² и більше. Проте у більшості технічних і фізичних задач похибка вимірювання сягає 1-10 %. Оскільки така похибка не залежить від математика, вона має назву неусувна.

Похибка методу пов'язана з тим, що точні оператори і вихідні дані заміняються наближеними. Наприклад, інтеграл заміняють сумою, похідну – різницею, функцію – багаточленом або будують нескінченний ітераційний процес і обривають його після кінченого числа ітерацій. Методи будуються так, що похибка наближається до нуля. Тобто цю похибку можна регулювати.

Похибку методу доцільно обирати так, щоб вона була в 2-5 разів менша неусувної похибки. Більша похибка знижує точність відповіді, а помітно менша не вигідна, адже значно збільшується обсяг обчислень.

Обчислення на ПЕОМ виконуються з певним числом значущих цифр. Це привносить у відповідь похибку округлення, яка накопичується в процесі обчислень.

Абсолютна та відносна похибка.

Абсолютною похибкою Δ наближеного числа а називається абсолютна величина різниці між відповідним числом А та числом а, тобто

Граничною абсолютною похибкою Δ_а наближеного числа розуміється всіляке число, не менше абсолютної похибки цього числа.

Тобто точне число Δ_а досить широке. Практично досить зручно в якості граничної абсолютної похибки обирати якомога менше число, яке задовольняє нерівності.

Абсолютної похибки н досить для характеристики точності вимірювань чи обчислень. Наприклад, при вимірюванні довжини двох стержнів отримали результати l₁ = 100,8 см ± 0,1 см чи l₁ = 10,2 см ± 0,1 см, то не дивлячись на збіг граничних абсолютних похибок, якість першого вимірювання більша, ніж другого. Для точності даних вимірювання суттєва абсолютна похибка, віднесена до одиниці довжини – відносна похибка.

Відносною похибкою δ наближеного числа а називається відношення абсолютної похибки Δ цього числа до модуля відповідного точного числа А () тобто

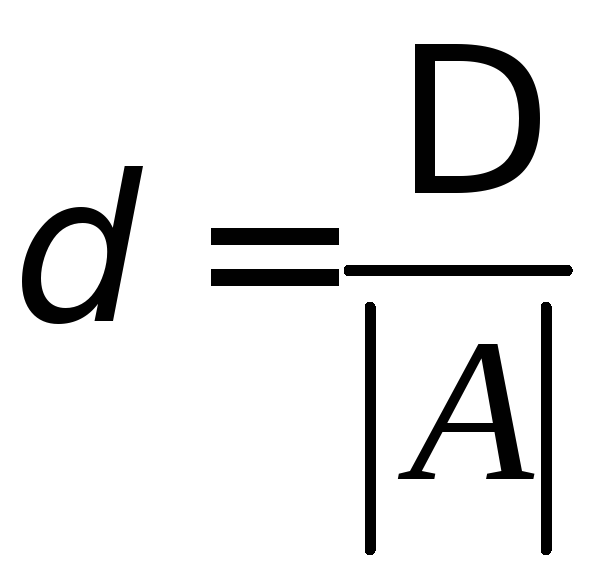, звідси .

Аналогічно, як у випадку абсолютної похибки вводяться поняття граничної відносної похибки δ_а:

тобто

звідки

Таким чином, за граничну абсолютну похибку числа а можна приймати:

.

За умови, що на практиці , часто використовують

.

1. Теорія похибок наближених розрахунків

Похибка суми.

Абсолютна похибка алгебраїчної суми декількох наближених чисел не перевищує суми абсолютних похибок цих чисел.

Нехай х₁, х₂,… х_n – данні наближені числа. Розглянемо алгебраїчну суму

Очевидно, що

Тоді

Наслідки:

За граничну абсолютну похибку алгебраїчної суми можна прийняти суму граничних абсолютних похибок

(*)

Звідси витікає, що гранична абсолютна похибка суми не може бути меншою за граничну абсолютну похибку найменш точного з доданків (тобто того, що має найбільшу похибку). Отже, з яким би ступенем точності не були всі інші складові, ми не можемо за їх рахунок збільшити точність суми. Тому немає сенсу зберігати зайві знаки і в більш точних складових.

Якщо доданки одного й того самого знаку, то гранична відносна похибка їх суми не перевищує найбільшої з граничних відносних похибок доданків.

Позначимо: – точні значеннях_і

– точне значення суми.

Тоді за граничну відносну похибку суми можна прийняти

Нехай є найбільшою з, тобто

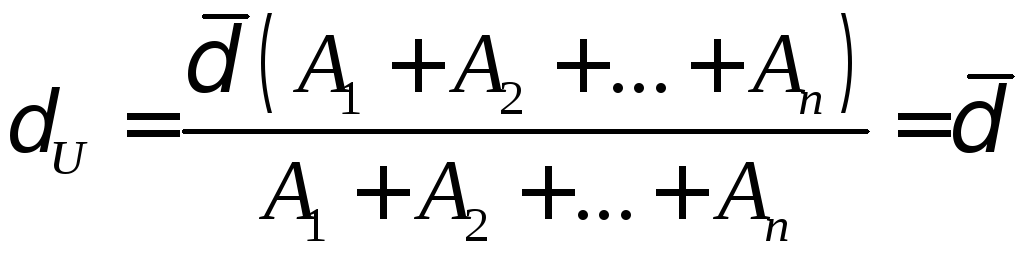
Тобто

Похибка різниці.

Роздивимось різницю двох наближених чисел . Тоді за формулою (*) гранична абсолютна похибка різниці

Тобто, гранична абсолютна похибка різниці дорівнює сумі граничних абсолютних похибок зменшуваного і від'ємника.

Звідси гранична відносна похибка різниці

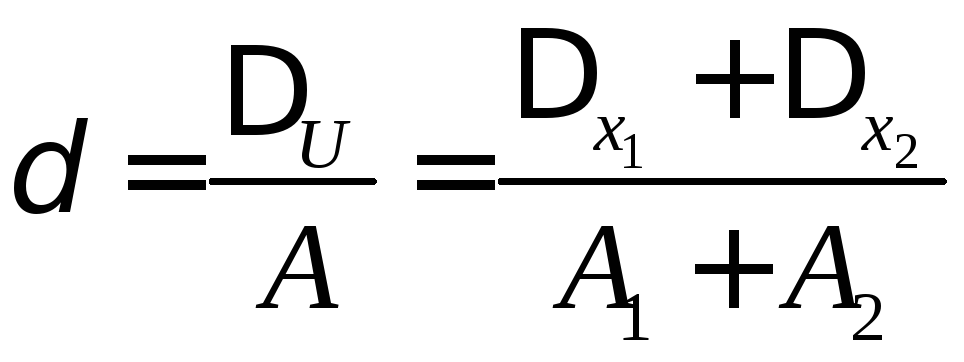
А – точне значення абсолютної величини різниці та.

Зауваження щодо втрати точності: Якщо наближені числа тадостатньо близькі одне до одного і мають малі абсолютні похибки, то числоА мале.

Гранична відносна похибка в цьому випадку може бути досить великою, у той час як відносні похибки тазалишаються малими, тобто тут має місце втрата точності.

Приклад: Обчислимо різницю двох чисел ікожне з яких має п'ять вірних знаків .

Тобто різниця U має лише дві значущі цифри, з яких остання сумнівна через те, що гранична абсолютна похибка різниці

Граничні відносні похибки зменшуваного, від'ємника і різниці

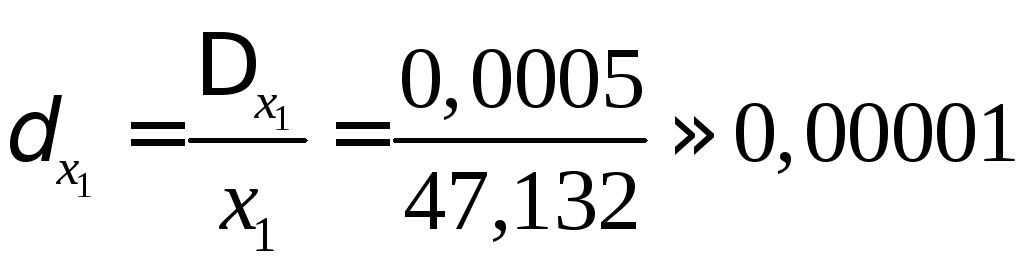
Гранична відносна похибка різниці тут в свою чергу приблизно в 5000 разів більше граничних відносних похибок вихідних даних. Тому при наближених обчисленнях корисно перетворювати вирази, в яких віднімаються близькі числа.

Приклад: знайти різницю

з трьома вірними даними

;

Цей результат можна отримати, якщо записати вихідні вирази у вигляді

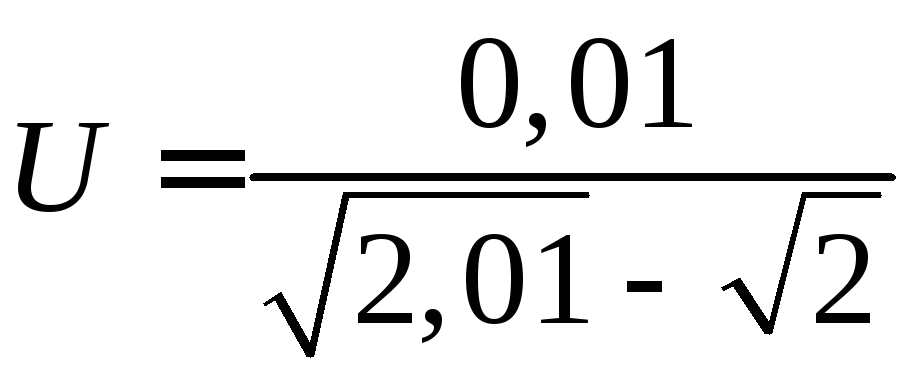
і вирахувати корені з трьома вірними знаками

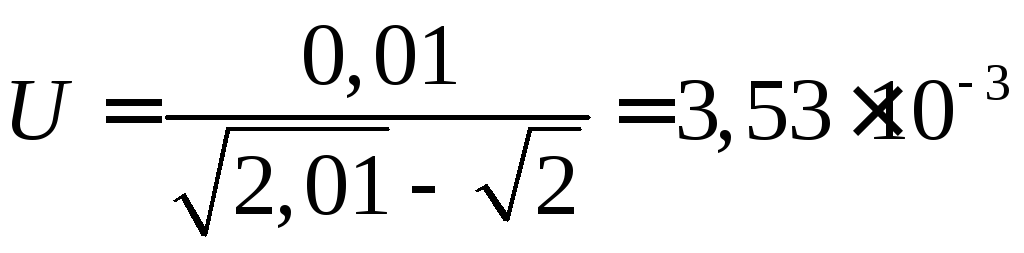
Отже при наближених обчисленнях потрібно по можливості уникати віднімання двох майже рівних наближених чисел (або зменшуване і від'ємник брати з достатньою кількістю запасних вірних знаків).

Похибка добутку.

Відносна похибка добутку декількох наближених чисел, не рівних нулю, не перевищує суми відносних похибок цих чисел.

Нехай . Нехай для простоти

Звідки використовуючи наближену формулу

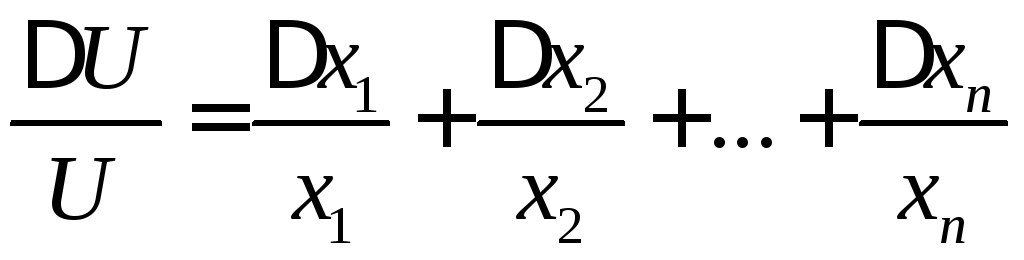
Тоді для відносних похибок

Отже гранична відносна похибка добутку

Граничну абсолютну похибку можна визначити через граничні відносні

.

Похибка частки.

Якщ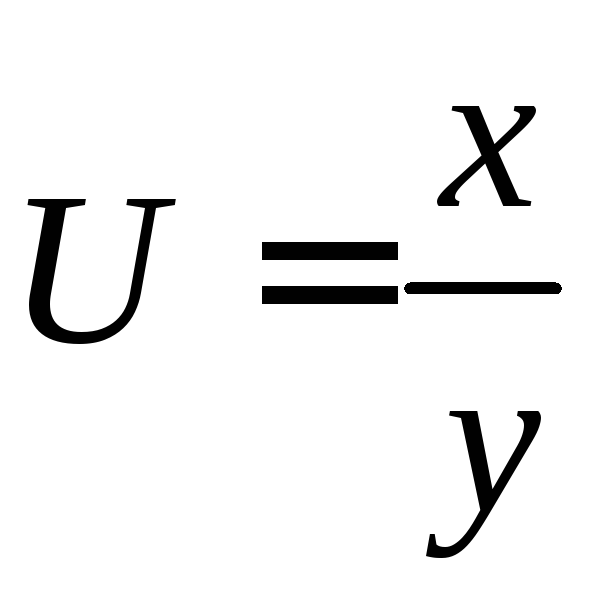о , то

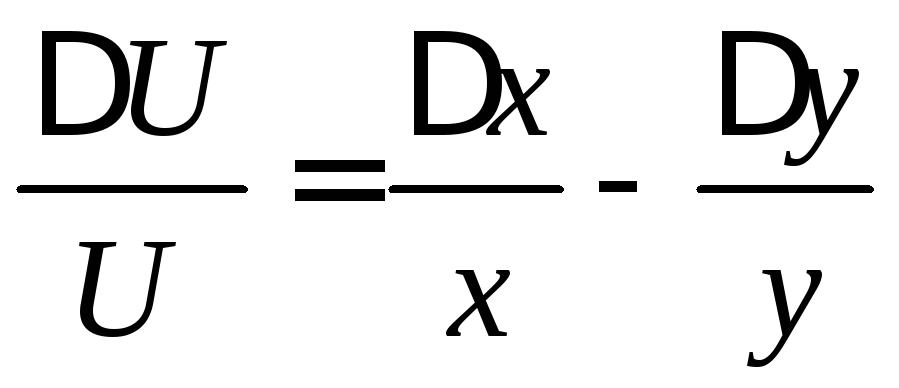
Тобто відносна похибка частки не перевищує суми відносної похибки діленого і дільника. Отже гранична відносна похибка

Відносна похибка степені.

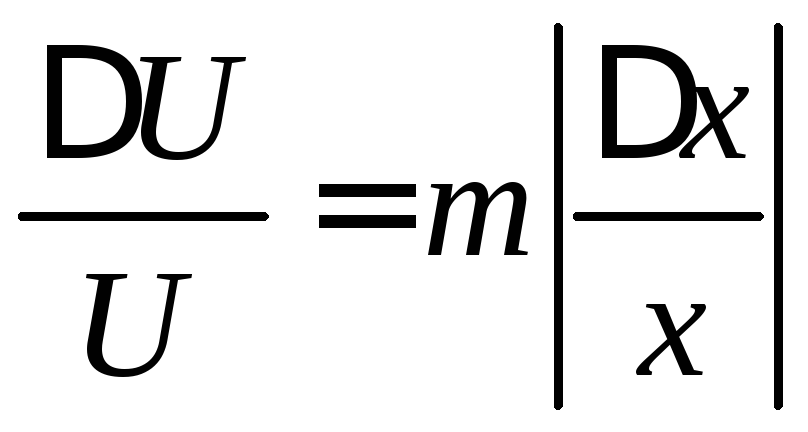
Тобто гранична відносна похибка m-ної степені числа в m разів більша граничної відносної похибки безпосередньо числа.