3. Кінцеві різниці. Інтерполяція

Кінцеві різниці різноманітних порядків

Нехай y = f(x) – задана функція. Позначимо через ∆x = h – фіксовану величину збільшення аргументу (крок). Тоді вираз

∆y = ∆f(x) = f(x+∆x) - f(x) (1)

називається першою кінцевою різницею функції y.

Аналогічно визначаються кінцеві різниці вищих порядків

∆ⁿy = ∆^n-1(∆y) n = 2, 3,…

Наприклад

∆²y = ∆[f(x + ∆x) – f(x)] = f(x + 2∆x) – f(x + ∆x) – f(x + ∆x) + f(x) =

= f(x + 2∆x) – 2f(x+∆x) + f(x)

Приклад. Побудувати кінцеві різниці для функції

Р(x) = x³

уважаючи ∆x = 1.

∆Р(x) = (х + 1)³ – х³ = х³ + 3х²·1 + 3х·1³ + 1³ – х³=3х² + 3х + 1

∆²Р(x) = 3(х + 1)² + 3(х+1) + 1 – 3х² – 3х – 1 =

= 3х² + 6х + 3 + 3х + 3 + 1 – 3х² – 3х – 1 = 6х + 6

∆³Р(x) = 6(х+1) + 6 – 6х – 6 = 6х + 6 + 6 – 6х – 6 = 6

∆⁴Р(x) = 6 – 6 = 0

∆⁴Р(x) = 0 при n > 3

Кінцева різниця третього порядку функції Р(x) постійна

Взагалі справедливо стверджування, якщо

Р(x) = а₀хⁿ + а₁х^n-1 - а₂х^n-2 +…+ а_n – поліном n-й степені, то

Символ Δ (дельта) можна розглядати як оператор, який ставить у відповідність функції функцію(∆x стале). Легко перевірити основні властивості оператора Δ:

1)

2)

3) ,

де m і n – цілі невід'ємні числа, причому за визначенням

З формули (1) будимо мати

Розглядаючи Δ як символічний множник, отримаємо

Примінивши це співвідношення n разів, будемо мати

.

Таблиця різниць

Нехай функція задана у вигляді таблицідля системи рівновіддалених точок,і = 0, 1, 2…, де .

Кінцева різниця послідовності визначається відповідностями

З першого рівняння маємо

Для подальшого перетворення необхідно звернутися до бінома Ньютона.

Біном Ньютона.

Розклад для цілих додатнихn було відомо до Ньютона. Йому належить смілива і досить плідна думка розповсюдити цей розклад і на випадок, коли n від'ємне і дробове.

де

Використовуючи формулу бінома Ньютона, отримаємо

Використовуючи тотожність

чи

Наприклад:

і так далі,

адже

Зауваження: для обчислення кінцевої різниці потрібно знатиn+1 членів даної послідовності.

Кінцеві різниці різноманітних порядків зручно розташувати в формі таблиці двох видів: горизонтальної таблиці різниць чи діагональної таблиці різниць.

Горизонтальна

x	y	Δy	Δ2y	Δ3y
x0	y0	Δy0	Δ2y0	Δ3y0
x1	y1	Δy1	Δ2y1	Δ3y 1
x2	y2	Δy2	Δ2y 2	Δ3y2
……………………………………………………………………………………....

Вертикальна

x	y	Δy	Δ2y	Δ3y
х0	y0	Δy0 Δy1 Δy2	Δ2y0 Δ2y1	Δ3y0
х1	y1
х2	y2
х3	y3

Приклад. Скласти горизонтальну таблицю різниць функції від початкового значенняз кроком.

.

x	Y	Δy	Δ2y	Δ3y
0	-1	3	8	12
1	2	11	20	12
2	13	31	32	12
3	44	63	44	12
4	107	107	56	12
5	214	163	68	12
……………………………………………………………………………………....

Через те, що наша функція – поліном третьої степені, то третя різниця її стала і рівна:

.

Тому подальше заповнення таблиці можна виконувати з допомогою додавання, використовуючи формули:

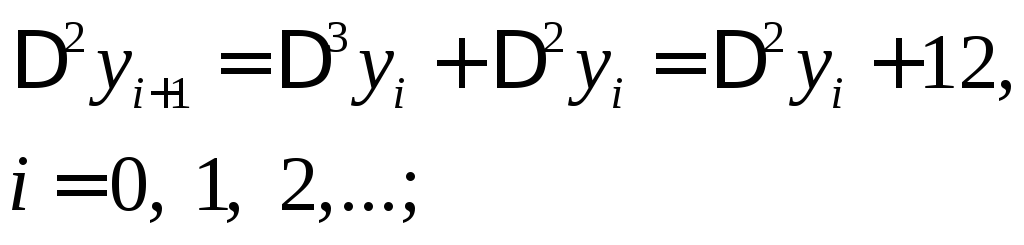
Зауваження: Навіть незначна помилка у обчисленнях у значенні функції призводить до значної помилки в її різницях високого порядку.

Узагальнена степінь.

Визначення: узагальненою n-степінню числа х називається добуток n множників, перший з яких дорівнює х, а кожен наступний на h менше попереднього

h – фіксоване стале число.

Вважають .

При узагальнена степінь співпадає зі звичайною. Обчислюють кінцеві значення для узагальненої степені; вважаючи

Визначимо другу різницю

Методом математичної індукції легко довести загальну формулу

k = 1, 2, …n.

при k > n.

Перша інтерполяційна формула Ньютона.

Нехай для функції задані значеннядля рівновіддалених значень незалежної змінноїі = 0, 1, 2,…n, де h – крок інтерполяції. Потрібно підібрати поліном степені не вищеn, який приймає в точках х значення

(1)

Умови (1) еквівалентні тому, що

при m = 1, 2, …n,

Слідуючи Ньютонові шукати поліном у вигляді

Шукана узагальнена степінь

(*)

Потрібно визначити коефіцієнти .

Вважаючи отримаємо з (*)

Для визначення коефіцієнта складемо першу кінцеву різницю

При

Для визначення складемо кінцеву різність другого порядку

.

При

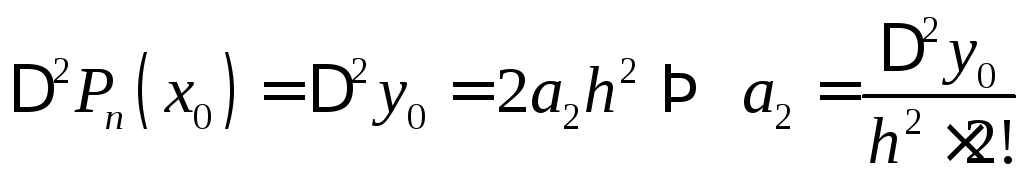
Послідовно продовжуючи цей процес, можна отримати

, 0! = 1, .

Підставляючи знайдені значення у вираз (*) отримаємо інтерполяційний поліном Ньютона:

(**)

Неважко помітити, що поліном (**) повністю задовольняє вимогам поставленої задачі: степінь його не віще n і .

Крім того,

При формула (**) перетворюється у поліном Тейлора для функціїу.

Дійсно

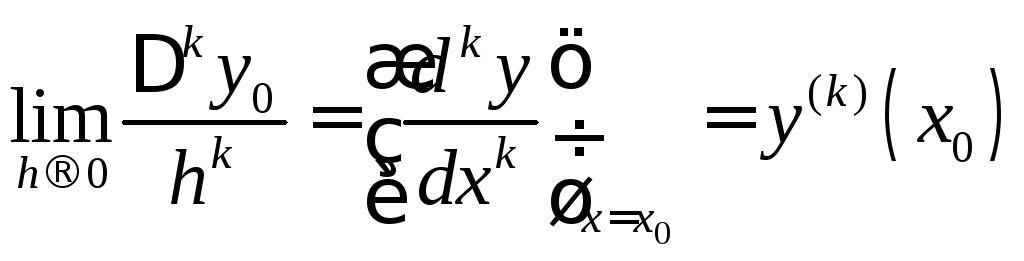
Крім того, очевидно

Звідси при формула (**) приймає вигляд полінома Тейлора

Для практичного використання інтерполяційну функцію формулу Ньютона (**) зазвичай записують у певним чином перетвореному вигляді. Для цього введемо нову змінну q, яка визначається формулою

Тоді

=

=

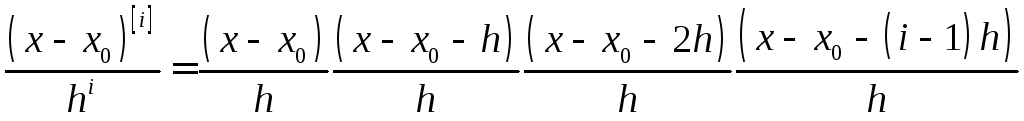Підставляючи ці вирази у формулу (*) матимемо

(***)

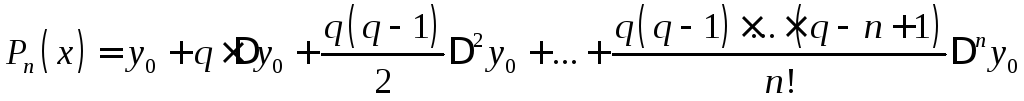де – кількість членів, необхідних для досягнення точких₀. це і є остаточний вигляд першої інтегральної функції Ньютона.

Формулу (***) вигідно використовують для інтерполювання функції в околі початкового значеннях₀, де q мале за абсолютною величиною.

Якщо в формулі (***) вважати n = 1, то отримаємо формулу лінійного інтерполювання

,

при n = 2 будемо мати формулу параболічного чи квадратичного інтерполювання

.

Якщо дана необмежена таблиця значень функції у, то число n в інтерполяційній формулі може бути будь-яким. Практично число n в цьому випадку і обирають так, щоб різниця була сталою із заданою степінню точності. За початкове значеннях₀ можна приймати будь-яке табличне значення аргументу х.

Якщо таблиця значень функції конечна, то число n обмежене: n не може бути більше числа значень функції у, зменшеного на одиницю.

Зауважимо, що при застосуванні першої інтерполяційної формули Ньютона зручно користуватися горизонтальною таблицею різниць, так як тоді потрібні значення різниць функції знаходяться у відповідних горизонтальних строках таблиці.

Приклад. Прийнявши крок h = 0,05, побудувати на відрізку [3,5; 3,6] інтерполяційний поліном Ньютона для функції , заданої таблицею

х	3,50	3,55	3,60	3,65	3,70
у	33,115	34,873	36,598	38,475	40,447

Складемо таблицю різниць:

х	y	Δy	Δ2y	Δ3y
3,50	33,115	1,698	0,084	0,005
3,55	34,813	1,785	0,092	0,003
3,60	36,598	1,877	0,095
3,65	38,475	1,972
3,70	40,447

…………………………………………

…………………………………………

Оскільки різниці третього порядку майже сталі, то в формулі вважатимемо n = 3. Прийнявши х₀ = 3,50, у₀ = 33,115 будемо мати:

чи

де

Приклад.

В таблиці наведені значення інтегралу імовірності

Використовуючи першу інтерполяційну функцію Ньютона, наближено знайти Ф(1,43).

Доповнюємо таблицю кінцевих різностей функції у до третього порядку включно

х	Y	Δy	Δ2y	Δ3y
1,0	0,8427	0,0375	-0,0074	0,0010
1,1	0,8802	0,0301	-0,0064	0,0010
1,2	0,9103	0,0237	-0,0054	0,0009
1,3	0,9340	0,0183	-0,0045	0,0009
1,4	0,9523	0,0138	-0,0036	0,0009
1,5	0,9661	0,0102	-0,0027	0,0005
1,6	0,9763	0,0075	-0,0022	0,0006
1,7	0,9838	0,0053	-0,0016	0,0004
1,8	0,9891	0,0037	-0,0012
1,9	0,9928	0,0025
2,0	0,9953

За х₀ приймаємо найближче табличне значення до шуканого значення х = 1,43, тобто вважатимемо х₀ = 1,4. Так як h = 0,1, то .

Підставимо в формулу (***)

Табличне значення:

Ф(1,43) = 0,9569 (згідно з джерелом «Таблиці функцій» Янке і Едме).

На практиці часто зустрічається необхідність для функції, заданої таблично ,підібрати аналітичну форму, що являє собою с певною точністю данні табличні значення функції. Така формула називається емпіричною, причому задача побудування її не однозначна.

При використанні емпіричної формули потрібно враховувати загальні властивості функції. Якщо з табличних різниць буде виявлено, що nі різниці функції для рівновіддалених значень аргументна сталі, то в якості емпіричної формули можна взяти відповідну інтерполяційну формулу Ньютона.

Приклад. Побудувати емпіричну формулу для функції у, заданої таблицею

х	0	1	2	3	4	5
у	5,2	8,0	10,4	12,4	14,0	15,2

Побудуємо таблицю різниць задля тог, що переконатися, що друга різниця стала:

х	Y	Δy	Δ2y
0	5,2	2,8	-0,4
1	8,0	2,4	-0,4
2	10,4	2,0	-0,4
3	12,4	1,6	-0,4
4	14,0	1,2
5	15,2

Використовуючи інтерполяційну формулу Ньютона в формі (***) і враховуючи, що h = 1, будимо мати

чи

Друга інтерполяційна формула Ньютона.

Перша інтерполяційна формула Ньютона практично не зручна для інтерполювання функції коло кінця таблиці. В цьому випадку зазвичай приміняться друга інтерполяційна формула Ньютона.

Виведемо її.

Нехай маємо систему значень функції

для рівновіддалених значень аргументу .

Побудуємо інтерполюючий поліном у вигляді:

Чи використовуючи узагальнюючу степінь.

4. ІНТЕРПОЛЯЦІЙНІ ФОРМУЛИ НЬЮТОНА І ЛАГРАНДЖА, НАБЛИЖЕННЯ СПЛАЙНАМИ

Інтерполяція.

Найпростіше завдання інтерполювання в наступному. На відрізку [а, b] задані точки x₀, x₁,…x₄, які мають назву вузли інтерполяції, і значення деякої функції f(x) в цих точках f(x₀) = y₀, f(x₁) = y₁,… f(x_n) = y_n (1)

Необхідно побудувати функцію F(x) (інтерполяційна функція), що належить відомому класові і приймає в вузлах інтерполяції ті самі значення, що f(x), тобто таку, що

F(x₀) = y₀, F(x₁) = y₁,… F(x_n) = y_n (2).

Теоретично це означає, що потрібно знайти кривуy = F(x) деякого певного типу, що проходить через завдану систему точок M_i (x_i, y_i), і = 0, 1,… (рис.)

В такій загальній постановці задача може мати незліченну множену рішень чи зовсім не мати їх.

Проте, задача стає однозначною, якщо замість довільної функції F(x), шукати поліном Р_n(x) степені не вище n, що задовольняє умови (2) ,тобто такої, що

Р(x₀) = y₀, Р(x₁) = y₁,… Р(x_n) = y_n.

Отриману інтерполяційну формулу y = F(x)

Зазвичай використовують для наближеного обчислення значень даної функції f(x) для аргументу х, відмінних від вузлів інтерполювання.

Для знаходження коефіцієнтів полінома

можна записати систему рівнянь

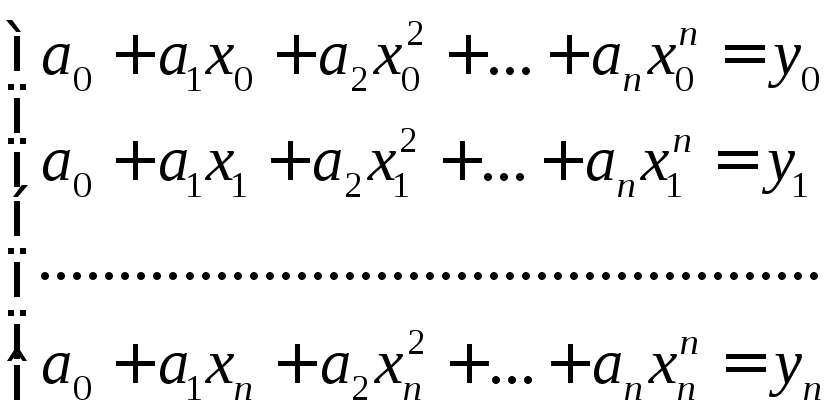(3)

Визначник цієї системи є так званий визначник Ван-дер-Монда

(4)

Отже, система (3) має єдине рішення.

Вирішивши цю систему(наприклад, за формулами Крамера чи методом Гауса) знайдемо інтерполяційний поліном.

Ітераційний поліномЛагранжа.

Нехай на відрізку [a, b] дані n+1 різних значень аргументу x₀, x₁,… x_n і відомі відповідні значення y₀, y₁,… y_n. Необхідно побудувати поліном L_n(x) степені не вище n, що має в завданих вузлах x₀, x₁,…x_n ті самі значення y₀, y₁,… y_n, тобто такі, що L_n(x_і) = y_і, і = 1, 2,…n. Вирішимо спочатку часткову задачу: побудуємо поліном Р_і(x) такий, що

Р_і(x_j)=0, при іР_і(x_і)=1 (5)

Так як шуканий поліном обертається в нуль в n точках x₀, x₁,… x_і-1, x_і+1,…x_n, то він має вигляд

, (6)

де .

Сталу можна визначити, якщо покластиx=x_і, тоді

, та

(7)

Підставивши (7) в (6) матимемо

(8)

Тепер можна вирішити загальну задачу: знайти поліном L_n(x) такий, що

.

Цей поліном має вигляд (9).

Насправді, по-перше, очевидно, побудованого полінома L_n(x) не вище n, і по-друге, з урахуванням (5), маємо

(j = 0, 1, …n).

Підставивши в (9) значення Р(x_і) з (8) матимемо

.

Це і є інтерполяційний поліном Лагранжа.

Приклад 1.

n = 1, тоді

Приклад 2.

n = 2, тоді

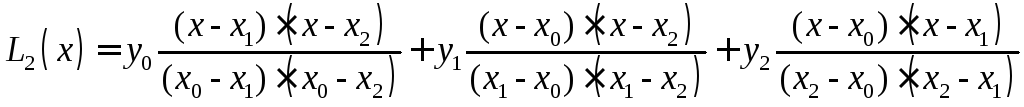
Приклад 3.

n = 3, тоді

Інтерполяція сплайнами.

Коли необхідно провести графік функції по відомим точкам y(x_i), зазвичай користуються лекалом. Проте, якщо точки розташовуються рідко, то досить важко підібрати ділянку лекала, яка б проходила відразу через багато точок. Тоді досвідчені інженери беруть залізну лінійку, ставлять її на ребро й згинають, притримуючи в декількох місцях так ,щоб її ребро проходило відразу через всі точки.

Цей спосіб інтерполяції можна описати математично. Гнучка лінійка – це пружний брусок; з курсу опору матеріалів відомо ,що рівняння його вільної рівноваги є . Отже, в проміжку між кожною парою сусідніх вузлів інтерполяційна функція є багаточленом третьої степені, який зручно записати у вигляді

(1)

.

Коефіцієнти багаточлена визначаються на кожному інтервалі з умов у вузлах. Очевидно, в вузлах багаточлен повинен приймати табличні значення функції:

(2)

(3)

Кількість цих рівнянь вдвічі менша кількості невідомих коефіцієнтів, тому для певної задачі необхідні додаткові умови. Для їх отримання знайдемо першу і другу похідні багаточлена (1)

при

і вимагатимемо безперервності цих похідних (тобто гладкості лінійки) в усіх точках, включаючи вузли.

П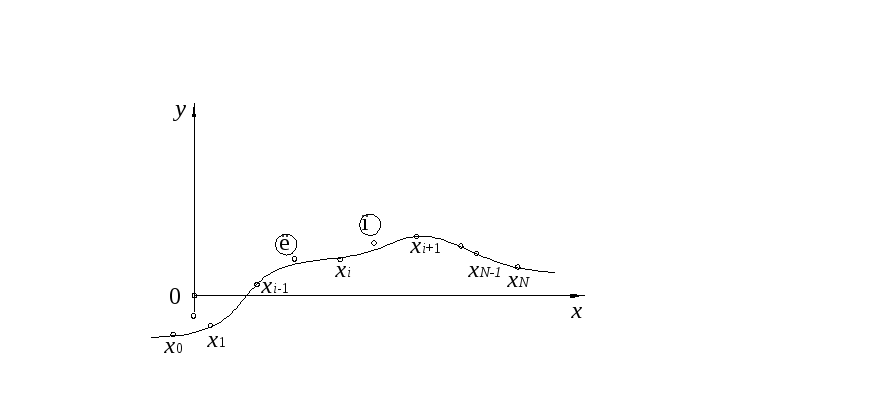рирівнюючи у внутрішньому вузліправу і ліву границі похідних, отримаємо:

(4)

(5)

Б

ракуючі дві умови зазвичай отримують з природного уявлення про низьку кривизну на кінцях:

(6)

Що відповідає вільно відпущеним кінцям лінійки. Проте якщо існують додаткові відомості про поведінку функції на кінцях, то можна записати інші крайові умови.

Рівняння (2) - (7) утворюють систему лінійних рівнянь для визначення 4N невідомих коефіцієнтів. Цю систему можна вирішувати методом виключення Гауса або іншим прямим чи ітераційним методом.