5. Метод найменших квадратів

До питання про відновлення функції за набором її значень можна підійти й по іншому. При побудові інтерполяційних формул ми вимагали точного збігу її значень в вузлах. Проте часто можна обмежитися вимогою мінімального відхилень цих значень від табличних. Наприклад, якщо значення y_i свідомо містять похибки чи простий вигляд апроксимуючої функції для нас важливіше точності, то такий підхід закономірний.

Нехай в наслідок експерименту ми отримали ряд величиниy: y₁, y₂,… y_n, відповідних значенням аргументу t₁, t₂,… t_n і нам необхідно встановити емпіричну залежність між y і t (рис 3).

Очевидно, якщо з’єднати послідовно всі ці точки, то матимемо ламану лінію, яка нічого спільного не матиме з шуканою залежністю y=f(t). Це витікає хоча б з того, що форма цієї ламаної не буде відтворюватися при повторних серіях вимірювань. Виміряні значення y_і будуть в загальному випадку зміщені відносно шуканої кривої y=f(t) як в бік більших, так і в бік менших значень, внаслідок статичного розкиду ( див. рис.).

Задача полягає в тому, щоб по заданих експериментальних точках провести криву (не ламану), яка проходила б якомога ближче до істинної функціональної залежності y=f(t). Теорії імовірності показує, що найкращим наближенням буде така крива ( чи пряма) лінія, для якої сума квадратів відстаней по вертикалях від точок до кривої буде мінімальною. Цей метод і має назву метод найменших квадратів.

Сутність методу.

Вважатимемо, що шукана залежність виражається функцією y=f(t, А₁, А₂,… А_m), де А₁, А₂,… А_m – параметри. Значення цих параметрів визначається так, щоб точки y_i розташовувались по обидва боки кривої y=f(t) якомога ближче до останньої ,тобто щоб сума квадратів відхилень виміряних значень y_i від функції y=f(t) була б найменшою. Це відповідає припущенню, що розкид точок y_i відносно кривої y=f(t) підпорядковується законові нормального розподілу. Як вже відмічалося вище, мірою цього розкиду є дисипація чи її наближений вираз – середній квадрат відхилень

(1)

і вимога мінімального розкиду відповідає вимозі мінімального значення цього середнього квадрату.

Відомо ,що функція приймає мінімальне значення, якщо перша похідна дорівнює нулеві, а друга похідна додатна. Для функцій багатьох змінних.

Таким чином, з умови мінімуму отримаємо систему рівнянь для визначення найкращих значень параметрів:

(2) і=1, 2,…m, m<n.

Зазвичай формулу залежності y=f(t, А₁, А₂,… А_m) задають у вигляді поліному

(3)

(m<n-1)

або у вигляді будь-якої іншої системи лінійно незалежних функцій

m<n (4)

яка досить добре передає загальний хід залежності y=f(t), який можна встановити за розташуванням точок (t_і, y_і).

У випадку вибору f(t, А₁, А₂,… А_m) в вигляді (3) рівняння (2) приймуть вигляд:

(і=0, 1, 2,…m) m<n-1

тобто

чи (і=0, 1, …m, m+1<n)

У випадку вибору розкладання f(t, А₁, А₂,… А_m) в формі (4) рівняння (2) приймають вигляд

тобто

або (і=1, 2, …m, m<n)

Рішення цих систем лінійних рівнянь дозволяє однозначно визначити коефіцієнти А_і розкладання y=f(t).

Рішення лінійних алгебраїчних рівнянь.

Отриманий дискретний аналог являє собою систему лінійних алгебраїчних рівнянь, яку можна вирішити або прямим, або ітераційним методом.

Прямими методами називаються такі методи, які дозволяють за кінцеве число дій отримати точне рішення системи. Слова «точне рішення» слід сприймати умовно як характеристику алгоритму, а не реального обчислювального процесу. Алгоритми, що лежать в основі простих методів, дають точне рішення, якщо всі величини в системі задані і всі обчислення проводяться абсолютно точно ,без похибок округлення. До прямих методів відносяться, наприклад, метод послідовного виключення невідомих Гауса.

Ітераційні методи засновані на побудуванні ітераційної послідовності, що сходиться до шуканого рішення. Обчислюючи певне число ітерацій і обриваючи процес, можна отримати наближене рішення системи з будь-якою попередньо завданою точністю.

Вибір в кожному окремому випадку метода рішення алгебраїчної системи визначається багатьма факторами: особливостями матриці А, порядком системи U, характеристикою ПЕОМ – швидкодією ,пам’яттю, ПО, ОС, характером задачі ,що вирішується.

Метод Гауса.

Метод послідовного виключення невідомих Гауса є одним з найбільш універсальних та ефективних методів рішення лінійних алгебраїчних систем. Він відноситься до числа прямих методів (тобто дозволяє за кінцеве число дій отримати точне рішення системи; «точне рішення» слід сприймати умовно як характеристику алгоритму, а не реального обчислювального процесу). Рішеня за методом Гауса складається з двох етапів. На першому етапі (прямий хід) система

(1) чи (1')

приводиться од трикутного вигляду.

На другому етапі (зворотній хід) іде послідовне визначення невідомих з трикутної системи.

Нехай .називаютьведучим елементом першого кроку. Якщо поміняємо місцями рівняння з номерами 1 таі, де . Система вважається невиродженою, такий номері завідомо знайдеться ,починаючи з другого. Для цього помножимо перше рівняння на і складемо його з другим, отримаємо

де

тобто

Після того помножимо перше рівняння на і складемо з третім. Отримаємо

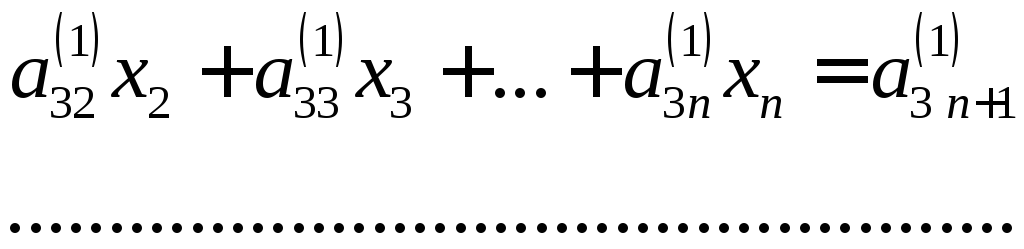
Аналогічно для окремих рівнянь системи від четвертого до n-го:

(2)

де

Основним результатом цього кроку є система n – 1 порядку з невідомими , утворена останніми (n – 1) рівняннями системи (2).

Тепер вважатимемо, що елемент ; який називаютьведучим елементом другого кроку, відмінний від нуля. У протилежному випадку потрібно провести відповідну перестановку рівнянь. Виключимо змінну з усіх рівнянь системи (2) починаючи з третього. Для цього помножимо друге рівняння ната складемо з третім, отримаємо

Потім помножимо друге рівняння на і складемо з четвертим, отримаємо

І так далі до n-ого рівняння

Таким чином, перетворена система (2) матиме вигляд

(3)

де .

Після n – 1-го кроку прийдемо до системи

(4)

Приведення вихідної системи до трикутного вигляду (4) завершує перший етап побудування рішення методом Гауса.

Другий етап – зворотній хід – полягає у рішенні трикутної системи (4). З останнього рівняння визначається . За знайденим значеннямзn – 1-го рівняння визначаємо . Потім заізn – 2-го рівняння визначають і так далі до 1-го рівняння, з якого визначають. На цьому процес побудови рішень системи (1) закінчується.

Для нашого дискретного аналогу рівняння теплопровідності метод рішення носить назву метод прогонки, в іноземній літературі метод Томаса, чи TDMA (три діагональний матриці алгоритм). Назва обумовлена групуванням невідомих коефіцієнтів матриці вздовж трьох діагоналей.

Наш дискретний аналог має вигляд

для вузлових точок на границі

чи

Суть алгоритму.

З першого рівняння відома залежність від, згідно другогозалежить віді, тобто враховуючи перше рівняння може бути виражене лише через. Виражаючи послідовночерездійдемо до необхідності виразити з останнього рівняннячерез. Проте так як в останньому рівнянніне існує, ми зразу отримаємо чисельне значення. Після знаходженнязворотною підстановкою знаходять всічерез.

Докладніше:

З першого рівняння

, де (5)

Підставимо в друге рівняння

,

де .

Аналогічно, підставивши в третє рівняння отримаємо залежність для і так далі до. У загальному вигляді

(6)

де (7)

Для останнього рівняння, маючи з передостаннього отримаємо

чи

(8)

Оскільки знайдений, то зворотною підстановкою за формулою (6) можна знайти

Алгоритм розрахунку.

1. обчислюємо по (5)

2. знаходимо по (7)

3. знаходимо 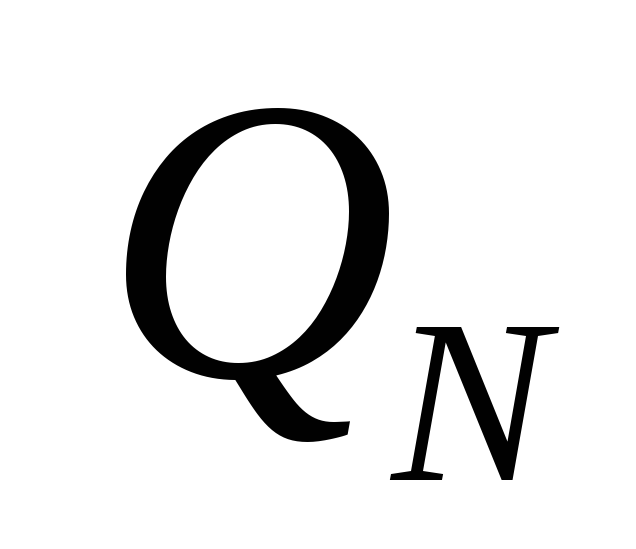і вважаємо по (8)

4. визначаємо дляпо (6).