
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
13.2 Komplexe Darstellung |
539 |
||||||
Der exakte Wert für das Überschwingverhalten beträgt |
|||||||
|
2 |
S0 |
π sin t |
dt − 1 ≈ |
0.1790. |
||
|
π |
|
t |
|
|||
An der Sprungstelle t0 konvergiert die Fourier-Reihe einer unstetigen Funktion f gegen den Mittelwert aus linksseitigem und rechtsseitigem Grenzwert. In einer Formel ausgedrückt bedeutet das
a0 |
∞ |
ak cos |
( |
k ω t0 |
) + |
bk sin |
( |
k ω t0 |
)) = |
|
2 |
||||||||||
+ kQ1 ( |
|
|
|
|
||||||
|
= |
|
|
|
|
|
|
|
|
|
lim f |
t |
) + |
|
lim f |
t |
) |
|
||||
t |
→ |
t0 |
+ |
( |
t |
→ |
t0 |
− |
( |
. |
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Auch wenn wir noch so viele Sinusund Kosinusglieder bei der Fourier-Reihe berücksichtigen, in der Nähe von Sprungstellen wird es immer eine gewisse Abweichung zwischen der Funktion und ihrer Fourier-Reihe geben. Das Gibbssche Phänomen hat somit auch Auswirkungen auf praktische Problemstellungen. Beispielsweise sind Artefakte, die bei der Bildkompression bei harten Farbübergängen auftreten, darauf zurückzuführen.
13.2 Komplexe Darstellung
Unter Zuhilfenahme der komplexen Zahlen lassen sich Fourier-Reihen kompakter darstellen. Auch die Formeln zur Berechnung der Fourier-Koe zienten gestalten sich mit komplexen Zahlen übersichtlicher. Reelle und komplexe Fourier-Reihen unterscheiden sich lediglich in der Art der Darstellung, inhaltlich unterscheiden sie sich nicht. Wir werden Formeln angeben, die den Zusammenhang zwischen der reellen und der komplexen Darstellung beschreiben. Das Verständnis der komplexen Darstellung von Fourier-Reihen ist grundlegend für die Fourier-Transformation in Kapitel 15.
13.2.1 Komplexe Fourier-Reihe
Mithilfe des Satzes von Euler, siehe Satz 11.1, kann man den Sinus und Kosinus mittels der komplexen e-Funktionen darstellen. Die entsprechenden Formeln stehen in Satz 11.2. Somit lässt sich eine Fourier-Reihe anstatt mit Sinus und Kosinus auch mittels komplexer e-Funktionen repräsentieren:
f |
t |
) = |
a0 |
∞ |
|
ak cos |
k ω t |
|
bk sin |
( |
k ω t |
|
|
|
|
|
|
||||||||
a0 |
|
|
|
e i |
|
|
|
||||||||||||||||||
|
( |
+ Q ( |
|
|
ei k( |
|
e) +i |
|
|
|
ei |
)) |
|
|
|
|
|||||||||
|
|
|
2 |
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
ak |
|
− |
|
|
|
bk |
|
|
|
− |
|
|
. |
||||
|
|
|
|
∞ |
|
|
|
k ω t |
k ω t |
|
|
k ω t |
|||||||||||||
|
|
|
2 |
k 1 |
|
|
|
ω t |
+2 |
|
|
|
|
− |
|
|
|
||||||||
|
|
= |
|
+ Q |
Π|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
‘ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 i |
|
|
|
||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nun fassen wir die e-Funktionen mit positivem und negativem Exponenten jeweils zusammen:
f t |
a0 |
∞ |
ak |
|
i bk |
ei k ω t |
|
ak |
|
i bk |
e |
|
i k ω t . |
|
|
|
− |
|
|
|
+ |
|
− |
||||||
2 |
k 1 |
‹ |
|
|
+ |
|
|
|
• |
|||||
( ) = |
|
+ Q |
2 |
|
|
|
2 |
|
|
|
||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|

540 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 Fourier-Reihen |
Um die Schreibweise weiter zu verkürzen, verwenden wir die Bezeichnungen |
|||||||||||||||||||
c0 |
= |
a0 , |
ck |
= |
ak |
− |
i bk |
, |
c |
k |
= |
ak |
+ |
i bk |
, |
k |
= |
1, 2, 3, . . . |
|
|
2 |
|
|
|
|
|
− |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
Wir arbeiten jetzt also mit komplexen Koe zienten ck, bei denen der Index k auch negative Werte annehmen kann: . . ., c−3, c−2, c−1, c0, c1, c2, c3, . . .. Damit erhalten wir
∞
f(t) = c0 + Q ‰ck ei k ω t + c−k e−i k ω tŽ . k=1
Nun zerlegen wir die Summe in zwei einzelne Summen und beachten die negativen Indizes in der zweiten Summe:
f |
t |
∞ ck ei k ω t |
∞ c |
k e i k ω t |
∞ ck ei k ω t |
−∞ ck ei k ω t |
|
∞ |
ck ei k ω t. |
|||||
|
( |
) = Q |
+ Q |
− |
− |
= Q |
+ Q |
= Q |
|
|||||
|
|
= |
0 |
= |
1 |
|
= |
0 |
k |
=− |
k |
=−∞ |
|
|
|
|
k |
k |
|
k |
1 |
|
|
||||||
Definition 13.5 (Komplexe Fourier-Reihe)
Die Darstellung einer Funktion f mit Periode T in Form einer unendlichen Summe
f |
t |
∞ |
ck ei k ω t, ω |
= |
2 π |
|
|
T |
|||||
|
( |
) = kQ |
|
|
||
|
|
=−∞ |
|
|
|
|
nennt man eine komplexe Fourier-Reihe mit Kreisfrequenz ω. Die komplexen Zahlen ck bezeichnet man als komplexe Fourier-Koe zienten.
Zwischen den reellen und den komplexen Fourier-Koe zienten besteht ein einfacher Zusammenhang. Es ist jederzeit möglich, die komplexen Fourier-Koe zienten aus den reellen Fourier-Koe zienten zu bestimmen und umgekehrt.
Komplexe und reelle Fourier-Koe zienten
Zwischen den reellen Fourier-Koe zienten ak, bk und den komplexen Fourier-Koe zienten ck besteht folgender Zusammenhang:
|
= |
2 Re(c0), |
|
|
|
= |
|
a0 |
|
|
|
|
a0 |
c0 |
|
ak |
2i,bk |
|
|
|
|||||
bk |
= |
2 Im(ck), |
c |
|
k |
= |
ak |
− i bk |
, |
k |
= 1, 2, 3, . . . |
|
ak |
|
2 Re ck |
, |
ck |
|
|
|
2 |
, |
k |
1, 2, 3, . . . |
|
|
= − |
( |
) |
|
− |
|
= |
|
+ |
|
|
= |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Für negative Indizes werden die komplexen Fourier-Koe zienten in der Regel gar nicht explizit betrachtet. Der komplexe Fourier-Koe zient mit dem Index −k ist ja gerade die konjugiert komplexe Zahl zum Fourier-Koe zienten mit dem Index k:
|
|
|
ak |
+ |
i bk |
|
ak |
− |
i bk |
|
|
|
|
c |
− |
k |
= |
|
= |
|
|
= |
ck. |
||||
|
|
2 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||

13.2 Komplexe Darstellung |
541 |
Trotzdem darf man die Fourier-Koe zienten mit negativen Indizes in der Summendarstellung in Definition 13.5 nicht unter den Tisch fallen lassen. Gerade das Zusammenspiel der komplexen Zahlen ck und c−k garantiert, dass in der Summe wieder eine reelle Funktion f entsteht. Nochmals: Die Funktion f ist nach wie vor eine reelle Funktion, auch in der Darstellung mit den komplexen Fourier-Koe zienten.
13.2.2 Berechnung komplexer Fourier-Koe zienten
Mit unserer bisherigen Vorgehensweise können wir die komplexen Fourier-Koe zienten nicht direkt aus einer periodischen Funktion bestimmen. Wir müssen zunächst die reellen Fourier-Koe zienten mit den entsprechenden Formeln berechnen und können daraus dann die komplexen Koe zienten erzeugen. Unser Ziel ist es nun, eine Formel herzuleiten, mit der man die komplexen Fourier-Koe zienten ck direkt aus einer Funktion f mit Periode T berechnen kann. Dazu verwenden wir die Integralformeln für ak und bk aus Satz 13.2:
|
ak |
i bk |
1 |
T |
|
|
|
|
|
|
|
|
i |
T |
|
|
|
|
|
||
|
2 |
|
|
|
cos |
|
|
dt |
|
2 |
|
|
sin |
|
k ω t dt. |
||||||
ck |
|
|
|
|
|
|
f |
t |
|
|
k ω t |
|
|
f |
t |
|
|
||||
= |
|
− |
= |
|
S− 2 |
) |
( |
− |
) |
( |
|||||||||||
|
|
T |
|
( |
|
) |
|
S− 2 |
( |
|
) |
||||||||||
|
|
|
2 |
|
T |
|
|
|
|
|
|
|
T |
T |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Beide Integrale erstrecken sich über dasselbe Integrationsintervall und lassen sich deshalb zu einem einzigen Integral zusammenfassen:
ck = |
1 |
T |
f(t) ‰ cos (k ω t) − i sin (k ω t)Ž dt. |
|
2 |
||||
|
|
S− T2 |
||
T |
||||
Unter Berücksichtigung der Symmetrieeigenschaften von Kosinus und Sinus fassen wir mit dem Satz von Euler beide Funktionen zu einer komplexen e-Funktion zusammen:
|
1 |
|
T |
|
|
|
|
|
|
|
|
|
|
1 |
|
T |
|
|
|
|
|
||
|
|
2 |
|
|
|
cos |
|
|
i sin |
|
|
dt |
|
2 |
|
|
e |
|
i k ω t dt. |
||||
ck |
|
|
|
|
f |
t |
|
|
k ω t |
|
k ω t |
|
|
|
f |
t |
|
|
|||||
= T |
|
− T2 |
) ( |
(− |
(− |
= T |
|
) |
− |
||||||||||||||
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
Diese Formel enthält auch den Spezialfall c0 = a20 . Denn für k = 0 vereinfacht sich der Integrand aufgrund von e0 = 1 zu f(t).
Satz 13.4 (Komplexe Fourier-Koe zienten)
Die komplexen Fourier-Koe zienten ck einer Funktion f mit Periode T und Kreisfrequenz ω = 2Tπ kann man mit den folgenden Formeln berechnen:
|
1 |
T |
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
e |
i k ω t dt, |
|
|
0, |
|
1, |
|
2, . . . |
|||
ck |
|
|
f |
t |
k |
|
|
|
||||||
= T |
= |
± |
± |
|||||||||||
|
S− T2 |
( |
) |
− |
|
|
|
|
||||||
Streng genommen erfolgt die Berechnung der komplexen Fourier-Koe zienten durch Integration einer Funktion mit komplexen Werten. Dieses Problem könnten wir umgehen, indem wir die komplexe Exponentialfunktion in Realund Imaginärteil zerlegen und beide Integrale getrennt berechnen. Allerdings ist es wesentlich eleganter, die imaginäre Einheit i bei der Integration wie eine reelle Konstante zu behandeln, siehe Beispiel 13.8.
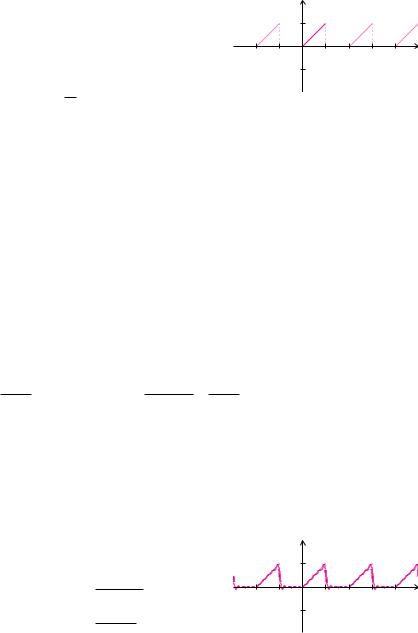
542 |
13 Fourier-Reihen |
Beispiel 13.8 (Komplexe Fourier-Koe zienten)
Der Prototyp einer 2 π-periodischen Funktion f ist definiert durch
f |
t |
|
0 |
für |
π |
t |
≤ |
0 |
) = œ |
t |
für |
−0 |
< t |
π . |
|||
|
( |
|
|
|
< |
≤ |
|
Die komplexen Fourier-Koe zienten ck bestimmen wir mit T = 2 π und ω = 2Tπ = 1 zu
|
f (t) |
π |
|
−2π −π |
π 2π 3π 4π t |
−π |
|
ck = |
1 |
π |
f(t) e−i k t dt = |
1 |
|
π |
|
S−π |
S0 |
t e−i k t dt. |
|||||
2 π |
2 π |
Die Funktion f ist zwischen π und 0 null. Somit können wir im Integral die Untergrenze 0 |
|||||
wählen. Das Integral können wir mithilfe der Stammfunktion |
|||||
|
|
|
|
ea x |
− |
x e |
a x |
dx = |
(a x − 1) , |
||
|
a2 |
||||
berechnen,S |
siehe Anhang A.5. Bisher haben wir solche Formeln nur mit reellen Parametern a |
||||
betrachtet. Wir vertrauen an dieser Stelle darauf, dass diese Formel auch für komplexe Zahlen a
richtig ist. Somit ergibt sich |
|
|
|
e−i k t |
|
i k t 1 |
|
|
|
|
|
|
e−i k π |
i k π 1 |
1 . |
|
||||||||||||||||||||||
ck |
|
|
|
e−i k t |
|
|
|
i k t 1 |
π |
|
|
|
|
π |
|
|
|
|||||||||||||||||||||
|
= |
|
|
|
|
(− − )W0 = |
|
|
( |
|
|
+ )W0 = |
|
( |
+ ) − |
|
|
|
||||||||||||||||||||
|
2 π i k 2 |
2 k2 π |
|
|
2 k2 π |
2 k2 π |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
k π |
|
|
|
|
|
|
|
|
verschiedenen Werte von k abwechselnd die Werte 1 und |
1. |
||||||||||||||||||||||
Der Ausdruck |
e(i− ) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
− |
|
|
liefert für die |
|
|
|
|
|
|
i k π |
|
|
|
|
|
k |
|
|
|
|
|
|
|
− |
||||||||||||||
Mit einer Formel ausgedrückt bedeutet das e− |
|
|
1= (− |
1 |
|
|
. Insgesamt erhalten wir damit |
|||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
k |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 k |
|
|
1) |
|
k |
|
|
|
|
|||||||||
ck |
= |
(− ) |
|
( |
|
|
+ |
1 |
) − |
|
|
= |
(− |
) − |
|
+ |
(− ) |
|
i. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
2 k2 π |
i k π |
|
|
|
2 k2 π |
|
|
2 k2 π |
|
|
|
|
2 k |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Diese Formel gilt für alle ganzen Zahlen k außer für k |
|
|
0. Den Fourier-Koe zienten c0 erhalten |
|||||||||||||||||||||||||||||||||||
wir aus dem Mittelwert |
m |
, der sich aus dem |
|
Flächeninhalt unter der Funktion über eine volle |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Periode bezogen auf die Länge der Periode ergibt: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
21 π2 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
m = c0 = |
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 π |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Die reellen Fourier-Koe zienten ak und bk lassen sich direkt aus den komplexen Fourier-Koe - zienten ck ermitteln:
a0 |
= |
|
2 c0 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 k 1 |
||||||
ak |
|
2 Re=ck |
|
|
|
||||||||
|
= |
|
|
( |
2 |
) |
= |
|
(−k) π− |
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
k 1 |
||||||
|
|
|
2 Im |
|
|
|
|
|
|
|
2 |
+ |
|
bk |
= |
− |
( |
ck |
) |
= |
|
(− ) |
|
||||
|
|
|
|
|
|
|
|||||||
k
π |
f (t) |
p9(t) |
|
|
|
−2π −π |
π 2π 3π 4π t |
|
−π |
|
|
Die reelle Fourier-Reihe lautet:
|
π |
|
2 |
|
1 |
|
1 |
|
|
1 |
1 |
|
||
f(t) = |
|
− |
|
‹cos (t) + |
|
cos (3t) + |
|
cos (5t) + . . |
.• + sin (t) − |
|
sin (2t) + |
|
sin (3t) . . |
.Ì |
4 |
π |
9 |
25 |
2 |
3 |
|||||||||
