
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

594 |
15 Fourier-Transformation |
15.6 Anwendungen
In der Elektrotechnik verwendet man die Fourier-Transformation zur Analyse von Schaltungen. Daraus hat sich die Systemtheorie entwickelt, mit der man ganz allgemeine, also auch nicht elektrische Systeme, analysieren kann. Wir erläutern in diesem Abschnitt die grundlegenden Begri e und Methoden der Systemtheorie und wenden sie auf einen Tiefpassfilter in der Elektronik an.
15.6.1 Lineare zeitinvariante Systeme
In den Ingenieurwissenschaften verwendet man die Systemtheorie zur Untersuchung technischer Prozesse und ihrer Gesetzmäßigkeiten. Bei einem System S hängen die Ausgabegrößen von den Eingabegrößen ab. Wenn das Ausgangssignal o durch das Eingangssignal i erzeugt wird, verwenden wir die Schreibweise
S
i(t) Ð→ o(t).
Ein System kann sehr komplex und aus vielen Teilsystemen zusammengebaut sein. Wir betrachten nur Systeme, bei denen zwischen den Eingangssignalen und den entsprechenden Ausgangssignalen ein linearer zeitinvarianter Zusammenhang besteht.
Definition 15.6 (Lineares zeitinvariantes System)
Bei einem linearen zeitinvarianten System S besteht zwischen den Eingangssignalen i1, i2 und den entsprechenden Ausgangssignalen o1, o2 ein linearer Zusammenhang:
S |
C1 o1(t) + C2 o2(t). |
C1 i1(t) + C2 i2(t) Ð→ |
Außerdem gilt bei einem solchen System zwischen einem Eingangssignal i und dem entsprechenden Ausgangssignal o für jede beliebige Zeitverschiebung t0
S |
o(t − t0). |
i(t − t0) Ð→ |
Lineare Systeme werden durch das Zusammenspiel von Einund Ausgabegrößen beschrieben. Bei vielen Systemen ergibt sich zwischen den Fourier-Transformierten der Einund Ausgangssignale ein einfacherer Zusammenhang als zwischen den Einund Ausgangssignalen im Zeitbereich. Deshalb betrachtet man das Verhältnis von Ausgangszu Eingangssignal im Frequenzbereich.

15.6 Anwendungen |
595 |
Definition 15.7 (Übertragungsfunktion) |
|
|
|||
Wenn o das Ausgangssignal eines linearen zeitin- |
i |
t |
|||
varianten Systems zum Eingangssignal i ist, dann |
|
× |
|||
ist die Übertragungsfunktion definiert durch |
|
× |
|||
( ) |
|||||
|
O f |
o |
×t |
||
G f |
|
|
|
|
Ö |
I |
(f ) |
|
|||
( ) = |
|
( ) |
|||
|
( ) |
|
|
||
Dabei sind I und O die Fourier-Transformierten von i und o.
cs I(f)
×
×
×
c s OÖf
( )
Grundsätzlich kann man ein Eingangssignal in entsprechend gewichtete und zeitverschobene Dirac-Impulse zerlegen. Aufgrund der Linearität und der Zeitinvarianz des Systems ist die Transformation der Summe der Dirac-Impulse leicht durchzuführen. Kennt man die Systemantwort auf einen Dirac-Impuls, dann ist das System komplett charakterisiert.
Definition 15.8 (Impulsantwort)
Bei einem linearen zeitinvarianten System bezeichnet man das Ausgangssignal g, das als Eingangssignal die Dirac-Distribution δ besitzt, als Impulsantwort:
S
δ(t) Ð→ g(t).
Zur Dirac-Distribution δ gehört die Fourier-Transformation 1 im Frequenzbereich: |
|||||||||||||
i |
t |
|
δ |
t |
|
c s |
I |
|
f |
|
1. |
||
|
( |
) = |
|
( |
) |
|
|
|
|
( |
|
) = |
|
Andererseits besitzt die Dirac-Distribution δ als Ausgangssignal die Impulsantwort g: |
||
o(t) = g(t) |
c s |
O(f) = G(f) I(f) = G(f) 1 = G(f). |
Impulsantwort und Übertragungsfunktion
Bei einem linearen zeitinvarianten System ist die Fourier-Transformierte der Impulsantwort g die Übertragungsfunktion G.
δ(t) |
c |
s |
|
1 |
|
|||
|
× |
|
|
|
|
|
× |
|
g |
× |
|
|
|
|
G |
× |
|
×t |
) |
c |
s |
×f |
) |
|||
|
( |
|
( |
|||||
|
Ö |
|
|
|
|
|
Ö |
|
Für ein beliebiges Eingangssignal i mit Ausgangssignal o gilt mit der Faltung, siehe
Satz 15.19
O(f) = G(f) I(f) s c o(t) = g(t) † i(t).
Sofern wir die Impulsantwort eines Systems kennen, sind wir in der Lage, das Ausgangssignal zu jedem beliebigen Eingangssignal durch Falten mit der Impulsantwort zu berechnen.
596 |
15 Fourier-Transformation |
Faltung mit der Impulsantwort
Das Ausgangssignal o zum Eingangssignal i berechnet man durch Falten mit der Impulsantwort: o(t) = g(t) † i(t).
i(t)
×
×
×
Ö
g(t) † i(t)
c |
s |
I(f) |
|
|
||||
|
|
|
|
|
× |
|
|
|
|
|
|
G |
f |
× |
|
f |
|
c |
s |
×I |
( |
) |
||||
( |
|
) |
|
|||||
|
|
|
|
|
Ö |
|
|
|
15.6.2 Tiefpassfilter
Idealerweise lässt ein Tiefpassfilter Signale mit niedrigen Frequenzen ungehindert durch und blockiert den Durchlass von Signalen mit hohen Frequenzen. In der Praxis schwächt ein Tiefpassfilter Signale mit niederen Frequenzen kaum ab, Signale mit höheren Frequenzen werden dagegen stark abgeschwächt.
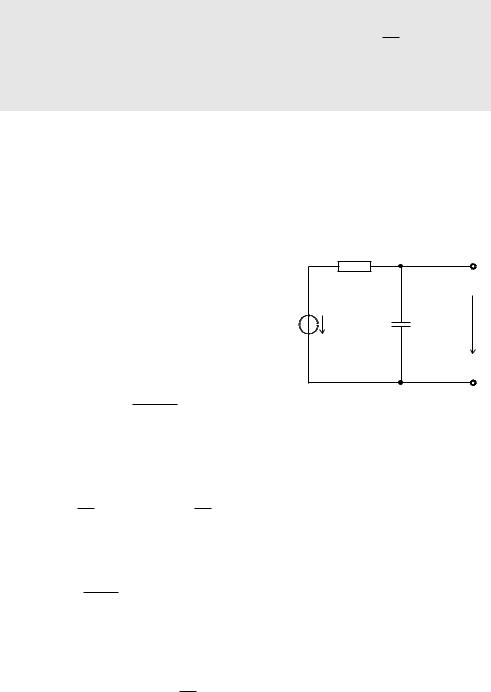
Ein einfacher Tiefpass in der Elektronik besteht aus einem Schaltkreis mit einem Ohmschen Widerstand R und einem Kondensator C. Unter idealisierten Annahmen stellt dieses RC-Glied ein lineares zeitinvariantes System dar. Zur Bestimmung der Übertragungsfunktion H verwendet man in der Elektrotechnik die Impedanzen am Widerstand und am Kondensator
1
ZR = R, ZC = . i 2 π f C
R |
|
|
u1(t) |
C |
u2(t) |
Zwischen der Fourier-Transformation der Eingangsspannung u1 und der Fourier-Transfor- mation der Ausgangsspannung u2 kennt man aus der Theorie elektrischer Schaltungen den Zusammenhang
u1(t) c |
sU1(f), u2(t) c |
sU2(f) Ô U2(f) = U1(f) |
ZC |
||||||||||||||||||||||
|
|
|
. |
||||||||||||||||||||||
ZR |
+ |
ZC |
|||||||||||||||||||||||
Dadurch erhalten wir die Übertragungsfunktion |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
U2 |
f |
ZC |
|
|
|
i 2 π f C |
|
|
|
|
|
|
|
|||||||||
G |
f |
|
U1 |
(f) |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||
|
ZR |
|
ZC |
|
R |
1 |
|
|
|
1 |
|
i 2 π f R C |
|
|
|
|
|||||||||
( |
|
) = |
|
|
( ) = |
|
+ |
|
= |
|
|
+ |
|
|
= |
|
+ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
i 2 π f C |
|
|
|
|
|
|
|
|||||||||||
Die Impulsantwort g ergibt sich aus der Korrespondenz aus Beispiel 15.3 und einer Ähn-
lichkeit mit dem |
Faktor a |
= |
1 |
, siehe Satz 15.8: |
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
R C |
|
s |
c |
1 |
1 |
|
t |
σ |
t |
|
g |
t |
|
. |
||||||||
G |
|
f |
1 |
|
i 2 π f R C |
|
R C e− R C |
|
|
|
||||||||||||||
|
( |
|
) = |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
( |
) = |
|
( |
) |
|
||
15.6 Anwendungen |
597 |
Wir berechnen nun, welche Ausgangsspannung u2 sich ergibt, wenn man als Eingangsspannung u1 eine Rechteckfunktion der Höhe 1 im Bereich zwischen 0 und t0 anlegt. Das Ausgangssignal berechnet man durch Falten der Impulsantwort g mit dem Eingangssignal u1, also
1 |
u1(t) |
|
|
|
|
|
t0 |
t |
u2(t) = g(t) † u1(t). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Falls t im Bereich zwischen 0 und t0 liegt, müssen |
|
|
|
|
|
|||||||||||||
wir g von 0 bis t integrieren: |
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
RC |
u1(t − τ ) |
|
||||||||
|
|
|
t |
1 |
1 |
|
|
= − |
1 |
|
U |
t |
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
u2 |
t |
0 R C e− R C τ |
dτ |
e− R C |
τ |
0 . |
|
|
|
|
g(τ ) |
|||||||
|
( |
) = S |
|
|
|
|
|
|
|
|
t |
− |
t0 |
t t0 |
τ |
|||
Das Einsetzen der Grenzen ergibt |
|
|
|
|
|
|
|
|
|
|||||||||
u2(t) = 1 − e− R1C t |
für 0 ≤ t ≤ t0. |
|
|
|
|
|
|
|
|
|||||||||
Für t-Werte größer als t0 erstreckt sich die Inte- |
|
|
|
|
|
|||||||||||||
gration von t − t0 tbis t1: |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
RC |
|
u1(t − τ ) |
|||||||
1 |
τ |
|
|
|
|
|
|
|
1 |
|
||||||||
u2 |
t |
t |
− |
t0 R C e− R C |
dτ. |
|
|
|
|
|
|
|
|
g(τ ) |
||||
|
( |
) = S |
|
|
|
|
|
|
|
|
|
|
|
|
t−t0 |
t0 t |
τ |
|
Mit derselben Stammfunktion wie im ersten Fall |
|
|
|
|
|
|||||||||||||
erhalten wir |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u2(t) = e− R1C (t−t0) − e− R1C t für t > t0.
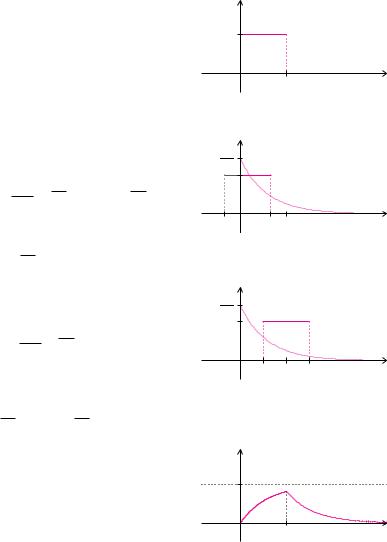
Die Ausgangsspannung wächst, solange die Eingangsspannung angelegt ist, streng monoton. Beim Zeitpunkt t0 wird die maximale Spannung 1 nicht ganz erreicht. Danach fällt die Ausgangsspannung monoton gegen null.
1 |
|
|
u2(t) |
t0 |
t |
