
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
7.4 Länge, Flächeninhalt und Volumen |
325 |
7.4 Länge, Flächeninhalt und Volumen
Integrale sind uns im Zusammenhang mit der Berechnung von Flächeninhalten bereits begegnet. In diesem Abschnitt werden wir sehen, dass sich Integrale auch zur Bestimmung von Längen und Volumina eigenen.
7.4.1 Flächeninhalte
Aufgrund des Hauptsatzes der Di erenzialund Integralrechnung wissen wir, dass man Flächeninhalte mithilfe von bestimmten Integralen berechnet. Dabei treten veschiedene Aspekte auf, die wir in diesem Abschnitt genauer betrachten. Dazu gehört etwa die Berechnung von Flächeninhalten bei Funktionen mit negativen Funktionswerten und die Berechnung von Flächeninhalten von Flächen, die durch das Schaubild von zwei Funktionen begrenzt werden.
Flächenberechnung
Die Fläche A, die das Schaubild einer nicht negativen Funktion f für x-Werte zwischen a und b mit der x-Achse einschließt, entspricht genau dem bestimmten Integral der Funktion f zwischen a und b:
bb
A = S f(x) dx = F (x)V = F (b) − F (a).
aa
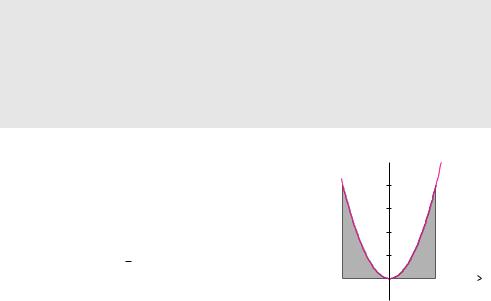
Beispiel 7.29 (Fläche zwischen x2 und der x-Achse)
Die Fläche, die die Funktion f(x) = x2 für x-Werte zwischen −2 und 2 mit der x-Achse einschließt, soll berechnet werden. Die Funktion f(x) = x2 hat keine negativen Funktionswerte. Außerdem können wir die Symmetrie der Funktion ausnutzen und die Berechnung auf das halbe Intervall beschränken. Mit der
Stammfunktion F (x) = 1 x3 ergibt sich der gesuch-
3
te Flächeninhalt zu
2 |
2 |
|
1 |
|
3 |
2 |
16 |
|
A = 2 S0 |
x |
dx = 2 |
|
x |
|
V0 = |
|
. |
3 |
|
3 |
||||||
f (x) = x2 y 
4
3
2
1
−3 −2 −1 |
1 2 3 |
x |
||||||||||||
|
||||||||||||||
Ì
In Beispiel 7.2 haben wir bereits gesehen, dass das bestimmte Integral bei einer Funktion mit negativen Funktionswerten nicht zwingend die Fläche berechnet, die die Funktion mit der x-Achse einschließt. Die Ursache liegt darin, dass das bestimmte Integral bei negativen Funktionswerten einen negativen Wert ergibt. Trotzdem ist die Lösung des Problems o ensichtlich. Wir bestimmen die Nullstellen der Funktion und zerlegen die gesamte Fläche in Bereiche, in denen die Funktion das Vorzeichen nicht wechselt.
326 |
7 Integralrechnung |
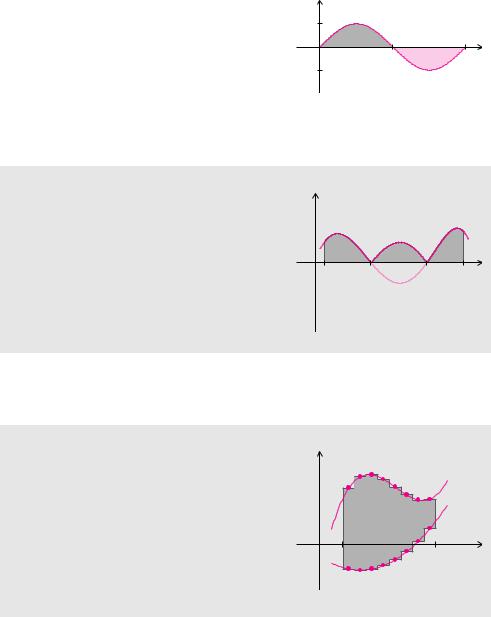
Beispiel 7.30 (Fläche zwischen sin x und der x-Achse)
Die Fläche, die der Graph der Funktion f x |
sin x |
y |
|
f(x) = sin x |
|
|||||||||||
für |
x |
-Werte zwischen |
0 |
und |
2π |
mit der |
x Achse ein- |
|
|
|
||||||
|
|
|
|
-( ) = |
|
1 |
|
|
|
|
||||||
schließt, soll berechnet werden. In dem betrachte- |
|
A+ |
|
|
|
|||||||||||
ten Bereich hat die Funktion die Nullstellen x0 |
0, |
|
|
|
|
|
||||||||||
x1 |
= |
π und x2 |
= |
2 π. Für x-Werte zwischen π und=2π |
−1 |
|
π |
A− |
2π x |
|||||||
ist |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
die Funktion negativ. Deshalb integrieren wir in |
|
|
|
|
|
||||||||||
diesem Bereichπüber − |
sin x Insgesamt ergibt sich |
|
|
|
|
|
||||||||||
|
. |
2π |
|
|
π |
2π |
= 4. |
|
|
Ì |
||||||
|
|
A = S0 |
|
sin x dx + Sπ |
(−sin x) dx = − cos xV0 |
+ cos xVπ |
|
|
||||||||
Flächenberechnung bei negativen Funktionswerten
Bei der Berechnung des Flächeninhaltes, den das Schaubild einer Funktion f mit der x-Achse bildet, benötigt man alle Nullstellen x0, x1, . . .
der Funktion im Intervall [a, b]. Auf Teilintervallen [xk, xk+1], in denen die Funktion negative Werte annimmt, integriert man über die negative Funktion
A+ = Sxk k+1 |
(−f(x)) dx. |
x |
|
y |
|
|
|
|
|
|
f(x) |
−f(x) |
f(x) |
|
|
|
|
|
|
|
|
|
A+ |
A+ |
A+ |
|
|
a |
xk |
|
xk+1 |
b |
x |
|
|
f(x) |
|
|
|
Wir betrachten nun Flächen, die durch das Schaubild von zwei Funktionen begrenzt werden. Auch in diesem Fall können wir die Berechnung des Flächeninhalts mithilfe von Integralen durchführen.
Fläche zwischen zwei Funktionen |
|
|
|
|
Den Flächeninhalt A der Fläche, die durch das |
y |
f(x) |
|
|
Schaubild der beiden Funktionen f und g für |
|
|
||
|
|
|
||
x-Werte zwischen a und b begrenzt wird, kann |
|
|
|
|
man durch |
|
|
|
|
A = Sa |
b |
|
|
|
(f(x) − g(x)) dx |
a |
b |
x |
|
berechnen. Dabei darf die Funktion f für alle |
|
g(x) |
|
|
x-Werte zwischen a und b nicht unterhalb der |
|
|
||
Funktion g verlaufen.
Die Gültigkeit dieser Formel machen wir uns durch eine Annäherung mit Rechtecksummen plausibel. Die Höhe der Rechtecke entspricht gerade der Di erenz der Funktionswerte. Also müssen wir über die Di erenz der beiden Funktionen integrieren. Die Nullstellen der beiden Funktionen spielen dabei keine Rolle.
7.4 Länge, Flächeninhalt und Volumen |
327 |
Das Berechnungsprinzip lässt sich auch anwenden, wenn die beiden Funktionen abwechselnd oberhalb oder unterhalb voneinander verlaufen. Man zerlegt dann die Fläche in Teilflächen zwischen den Schnittpunkten.
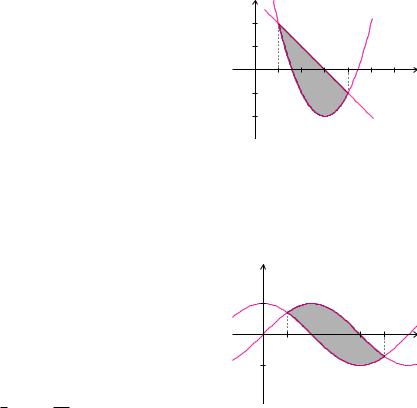
Beispiel 7.31 (Fläche zwischen zwei Funktionen)
a) Die Schaubilder der beiden Funktionen
f(x) = x2 − 6 x + 7, g(x) = 3 − x
begrenzen eine Fläche. Zur Bestimmung des Flächeninhalts A berechnen wir zunächst die x-Werte der Schnittpunkte der beiden Schaubilder. Die zwei x-Werte x1 = 1 und x2 = 4 sind die Lösungen der quadratischen Gleichung
x2 − 6 x + 7 = 3 − x.
y
f (x) = x2 − 6 x + 7
2
1
1 |
2 |
3 |
4 |
5 |
6 |
x |
−1
−2
g(x) = 3
Aus der Skizze erkennen wir, dass im Bereich von 1 bis 4 die Funktion g oberhalb von f verläuft. Somit berechnen wir den Flächeninhalt durch
|
= S |
4 |
‰( |
3 |
|
|
|
|
|
x2 |
− |
6 x |
+ |
7 |
)Ž |
dx |
= S |
4 |
+ |
5 x |
− |
4 |
Ž |
dx |
||||
A |
|
|
|
x |
|
|
x2 |
|||||||||||||||||||||
|
|
|
|
− ) − ( |
|
|
|
|
|
‰− |
|
|
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
5 |
|
2 |
|
|
4 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
= − |
|
x |
|
+ |
|
x |
|
− 4 x V1 |
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b) |
Wir betrachten die beiden Funktionen |
y |
|
|
|
|
|
||||||
|
f |
x |
sin x, |
|
g x |
cos x. |
f (x) = sin (x) |
|
|
|
|||
|
Die |
(Schaubilder) = |
dieser( ) =Funktionen haben zwar |
1 |
|
|
|
|
|
||||
|
unendlich viele Schnittpunkte, aus Symmetrie- |
1 |
|
|
5 |
|
x |
||||||
|
gründen haben aber alle Teilflächen zwischen |
π |
π |
π |
|||||||||
|
4 |
4 |
|
||||||||||
|
|
|
|
|
|
|
|||||||
|
diesen beiden Funktionen denselben Flächenin- |
−1 |
|
|
|
|
|
||||||
|
halt. Sinus und Kosinus haben für |
|
|
g(x) = cos (x) |
|
||||||||
|
x1 = |
π |
|
= |
5 π |
|
|
|
|
|
|
|
|
|
4 , |
x2 |
4 |
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
||
jeweils dieselben Werte, nämlich |
√2. Im Bereich von x1 |
bis x2 verläuft der Sinus ober- |
||||||
|
2 |
|||||||
halb vom Kosinus. Wir |
bestimmen den Flächeninhalt A einer einzigen Teilfläche. Dieser ist |
|||||||
|
± |
|
|
|
|
|
||
gegeben durch
|
= S4 |
5 π |
( |
|
− |
|
|
= (− |
|
− |
|
) U |
5 π |
A |
4 |
sin x |
cos x |
dx |
cos x |
sin x |
4 |
||||||
|
|
|
) |
|
|
|
4 |
||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
π |
= |
√ |
|
|
Ì |
2 2. |
||||
|
|
|
|
|
7.4.2 Bogenlänge
Unter der Bogenlänge versteht man die Länge, die das Schaubild einer Funktion hat. Dabei wird die Krümmung berücksichtigt. Wir können uns vorstellen, dass wir einen Faden entlang des Schaubildes legen, Anfang und Ende markieren und dann die Länge dieses Fadens mithilfe eines Lineals abmessen.

328 |
7 Integralrechnung |
Satz 7.15 (Bogenlänge)
Das Schaubild einer di erenzierbaren Funktion f für x-Werte zwischen a und b hat die
Bogenlänge
b »
L = S 1 + f′(x)2 dx.
a
Die Formel aus Satz 7.15 ist ein Spezialfall der allgemeinen Formel für die Bogenlänge einer parametrisierten Kurve, die wir in Kapitel 9 herleiten werden. Deshalb verzichten wir an dieser Stelle auf eine Herleitung. Allerdings führen wir ein paar Plausibilitätsbetrachtungen durch. Bei einer konstanten Funktion ist die Ableitung überall null und die Formel vereinfacht sich zu
|
|
b |
|
|
|
|
|
|
|
|
|
L |
|
dx |
|
b a. |
|
|
|
|
|
||
|
|
a |
|
|
|
|
m x c gilt |
|
|
|
|
Bei einer |
=linearen Funktion= − |
f x |
y |
|
|
||||||
S |
|
|
√ |
|
|
( ) = |
+ |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|||
L = Sa |
1 + m2 |
dx |
|
mb + c |
|
f(x) = mx + c |
|||||
|
|
|
|||||||||
|
|
√ |
|
|
|
|
|
|
|
|
|
|
= 1 + m2 (b − a). |
|
|
|
|
||||||
Das ist gerade der Abstand der beiden Punkte |
|
ma + c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
mit den |
Koordinaten |
( |
a |
S |
f |
( |
a |
|
|
|
und |
( |
b |
S |
f |
( |
b |
)) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
denn |
L = » |
|
|
|
|
|
|
)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
b x |
|||||||||||||||||||
|
|
|
|
= √ |
|
(b − a). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
(b − a)2 + (m b − m a)2 |
1 + m2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Beispiel 7.32 (Bogenlänge) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Die Bogenlänge des Schaubildes der Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
f (x) = cosh(x) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
cosh x, |
|
2 |
|
|
|
|
|
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||||||||||||||||
|
f |
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
berechnet( man) = |
mit |
− |
|
≤ |
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
»1 + sinh2 x dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
L = S−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Aufgrund der Symmetrie und wegen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
cosh2 |
2x − sinh2 x = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 −2 −1 |
1 2 3 |
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
gilt L |
|
|
|
|
|
|
02 |
|
2 sinh 2 |
|
|
e2 |
|
e−2 |
|
|
7.2537. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
2 |
0 |
|
cosh x dx |
= |
2 sinh x |
S |
= |
= |
− |
≈ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
|||||||||||||||||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
