
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

6.4 Geometrische Bedeutung der Ableitungen |
273 |
Steigung nimmt also auch zu, wenn sie sich von negativen Werten zu positiven Werten verändert. Den Begri der Krümmung kann man mathematisch noch exakter definieren. Im Zusammenhang mit Kurven geschieht dies in Abschnitt 9.4.
Beispiel 6.23 (Krümmung) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Das |
Krümmungsverhalten |
der |
|
Exponentialfunktion |
|
|
y |
|
|
|
|
||||||||||||||||||||
f x |
) = |
5 e− |
x2 |
bestimmt |
|
man |
|
anhand |
der |
zweiten |
|
|
5 |
f (x) = 5 e− |
x 2 |
||||||||||||||||
2 |
|
|
|
|
4 |
2 |
|||||||||||||||||||||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ableitung |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
′ |
|
|
|
5 x e |
− |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
f |
|
x |
|
2 |
5 x2 e |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
f |
|
|
(x) = −5 e |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
′′ |
( |
) |
= |
− |
− |
x2 |
+ |
|
|
|
|
|
− |
x2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
− |
x2 |
|
|
x2 |
|
|
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
= |
5 x2 |
|
|
e |
|
|
|
e |
|
|
2 . |
|
3 |
2 |
1 |
2 |
3 |
x |
||||||
|
|
|
|
|
|
|
5(x |
|
−1 |
|
)x |
+ |
1 |
) |
− |
|
1 |
||||||||||||||
|
|
|
|
|
|
|
= |
( |
− |
|
)( |
|
|
|
|
|
|
− |
− |
− |
|
|
|
|
|||||||
An den Stellen x |
|
1 wechselt das Krümmungsverhalten. Die Funktion ist für |
1 |
x 1 |
||||
rechtsgekrümmt |
und für x |
|
1 oder für x 1 linksgekrümmt. |
− < |
< |
|
||
|
= ± |
|
< − |
> |
Ì |
|||
|
|
|
|
|
|
|||
6.4.4 Lokale Extrema
Technische Systeme verfügen meistens über eine Vielzahl von Stellgrößen. Mithilfe mathematischer Modelle versucht man, für diese Stellgrößen Werte zu ermitteln, die zu einem optimalen Ergebnis führen. Beispielsweise versucht man Verbrennungsprozesse so zu steuern, dass möglichst wenig Schadsto e erzeugt werden. Optimierungsprobleme spielen auch in anderen Bereichen eine wichtige Rolle. In der Betriebswirtschaft geht man etwa der Frage nach, bei welcher Anzahl produzierter Teile man einen maximalen Gewinn erzielen kann. Solche Fragestellungen führen zu dem mathematischen Problem, Stellen zu bestimmen, an denen Funktionen ihren minimalen oder maximalen Wert annehmen.
Definition 6.10 (Lokales Minimum und Maximum)
Eine Funktion f besitzt an der Stelle x0
Lein lokales Minimum, wenn alle anderen Funktionswerte in der Umgebung von x0 größer sind als der Funktionswert an der Stelle x0:
f(x0) < f(x), x ≠ x0.
Einen entsprechenden Punkt im Schaubild bezeichnet man als Tiefpunkt.
Lein lokales Maximum, wenn alle anderen Funktionswerte in der Umgebung von x0 kleiner sind als der Funktionswert an der Stelle x0:
f(x0) > f(x), x ≠ x0.
Einen entsprechenden Punkt im Schaubild bezeichnet man als Hochpunkt.
274 |
6 Di erenzialrechnung |
Ein lokales Minimum oder Maximum bezeichnet man auch als relatives Minimum oder Maximum. Minima und Maxima werden auch als Extrema bezeichnet.
Ein Minimum oder Maximum werden wir in der Regel an einer Stelle finden, an der das Schaubild der Funktion eine waagrechte Tangente hat. Allerdings ist zu beachten, dass Definiton 6.10 auch anstellen funktioniert, an denen die Funktion gar nicht di erenzierbar ist.
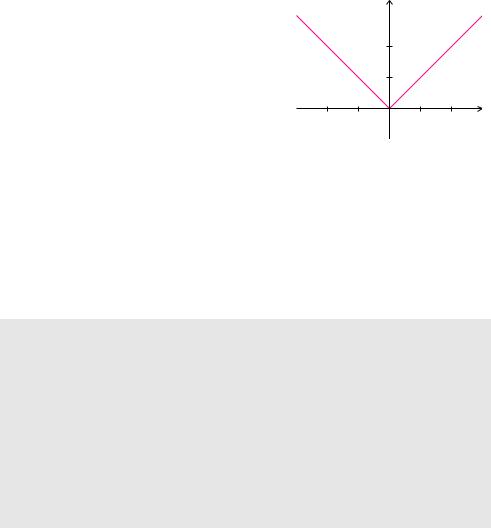
Beispiel 6.24 (Minimum der Betragsfunktion)
Die Funktion f(x) = SxS besitzt die Ableitung
f′ |
|
x |
1 |
für |
x |
< |
0 |
( |
−1 |
für |
x |
0. |
|||
|
|
) = œ |
|
|
> |
|
Die Ableitungsfunktion wird also niemals null. Trotzdem hat die Funktion an der Stelle x0 = 0 ein lokales Minimum. An der Stelle x0 = 0 ist f nicht di e- renzierbar, deshalb findet man dieses Minimum nicht durch die Bedingung f′(x) = 0.
|
|
y |
|
|
|
|
|
f (x) = |x| |
|
||
|
|
2 |
|
|
|
|
|
1 |
|
|
|
−2 |
−1 |
1 |
2 |
x |
|
Ì |
|||||
|
|
|
|
||
Definition 6.10 liefert uns noch kein Berechnungsverfahren für Extrema. Wir brauchen also weitere Bedingungen, die uns die Berechnung von Minima und Maxima ermöglichen. In der Mathematik unterscheidet man typischerweise drei Arten von Bedingungen. Notwendige Bedingungen sind Voraussetzungen, die auf jeden Fall erfüllt sein müssen, damit eine bestimmte Eigenschaft überhaupt möglich ist. Hinreichende Bedingungen garantieren, dass die Eigenschaft erfüllt ist. Bedingungen, die hinreichend und notwendig sind, bezeichnen wir als „genau-dann“-Bedingungen, siehe Abschnitt 1.1. Mithilfe der ersten und zweiten Ableitung können wir für Minima und Maxima alle drei Arten von Bedingungen formulieren.
Satz 6.12 (Bedingungen für ein Minimum)
Wenn eine di erenzierbare Funktion f an der Stelle x0
Lein lokales Minimum hat, dann besitzt sie dort eine waagrechte Tangente. Die Bedingung f′(x0) = 0 ist somit notwendig.
Leine waagrechte Tangente hat und zusätzlich links gekrümmt ist, dann hat sie dort ein lokales Minimum. Die Bedingung f′(x0) = 0 und f′′(x0) > 0 ist somit hinreichend.
Leine waagrechte Tangente hat und die Ableitung f′ beim Durchgang durch x0 das Vorzeichen von minus nach plus wechselt, so hat f genau dann an der Stelle x0 ein lokales Minimum. Diese Bedingung ist somit notwendig und hinreichend.

6.4 Geometrische Bedeutung der Ableitungen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
275 |
|||||||||||||||||||||||||||||||||||||
Beispiel 6.25 (Minimum) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Die Extremwerte der Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
f x 2 √x2 4 x 8 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bestimmen( )wir= |
aus den− |
|
Nullstellen+ − |
der ersten Ablei- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
tung |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
1 |
2 |
|
|
|
3 |
|
4 |
5 |
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2 2 x |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
f′ |
( ) = |
|
√ |
( |
|
− |
|
|
) |
|
|
= |
2 |
√ |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
f (x) =2√x2 |
|
4x + 8 6 |
||||||||||||||||||||||||||||||
|
x |
|
|
|
2 x2 4 x 8 |
|
|
|
x2 4 x 8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Der einzig mögliche |
Kandidat für einen Extremwert |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
− |
||||||||||||||||||||||||||||||||||||||
|
− |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ist somit x 2. Bei der ersten Ableitung wechselt an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
der Stelle x= |
2 das Vorzeichen von minus nach plus. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Also besitzt=die Funktion f an der Stelle x |
|
2 ein lokales Minimum. Der Tiefpunkt hat die |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Koordinaten |
|
2 |
|
|
2 |
. Wir können auch mit |
|
der zweiten Ableitung |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
( |
|
S − |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
2 |
|
|
2 x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
√x2 4 x |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
4 x 8 x 2 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
f |
|
|
x |
|
|
|
|
|
2 |
|
|
|
2 x2 |
|
4 x 8 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
− |
|
|
|
)( − |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
+ |
|
−4 |
|
√ |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− + |
|
|
|
|
|
|
− |
|
x + |
x |
8− ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
( ) = |
|
|
x |
|
|
|
4 x 8 |
2 |
x |
|
|
|
4 x 4 |
|
|
|
|
|
= |
8 |
» |
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x |
|
− |
|
x |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
− |
+ |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
= |
|
|
|
− + |
|
|
− |
|
+ |
|
|
|
− |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
x2 |
|
− |
4 x |
+ |
8 |
) |
3 |
|
|
|
|
|
( |
x2 |
− |
4 x |
+ |
8 |
) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
nachweisen, dass die Funktion f an der Stelle x = 2 ein Minimum hat, denn f′′(2) > 0. Allerdings ist diese Methode aufwendiger. Wesentlich eleganter ist die folgende dritte Methode zum Nachweis eines Minimums: Die beiden Grenzwerte
√
lim 2 x2 − 4 x + 8 − 6 = ∞
x→±∞
garantieren, dass die Funktion f mindestens ein lokales Minimum besitzt. Da wir andererseits aus der Betrachtung der ersten Ableitung bereits wissen, dass die Funktion f höchstens einen Extremwert besitzt, muss der Extremwert an der Stelle x = 2 ein Minimum sein. Ì
Die Bedingungen für ein Maximum lassen sich analog zu den Bedingungen für ein Minimum formulieren.
Satz 6.13 (Bedingungen für ein Maximum)
Wenn eine di erenzierbare Funktion f an der Stelle x0
Lein lokales Maximum hat, dann besitzt sie dort eine waagrechte Tangente. Die Bedingung f′(x0) = 0 ist somit notwendig.
Leine waagrechte Tangente hat und zusätzlich rechts gekrümmt ist, dann hat sie dort ein lokales Maximum. Die Bedingung f′(x0) = 0 und f′′(x0) < 0 ist somit hinreichend.
Leine waagrechte Tangente hat und wenn die Ableitung f′ beim Durchgang durch x0 das Vorzeichen von plus nach minus wechselt, so hat f genau dann an der Stelle x0 ein lokales Maximum. Diese Bedingung ist somit notwendig und hinreichend.

276 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 Di erenzialrechnung |
|||||||||||||||||||
Beispiel 6.26 (Minima und Maxima) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Die Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
4 x |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
|
|
|
|
|
||||
|
|
f(x) = |
|
|
|
4 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1+x2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
besitzt die |
Ableitung |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
x2 |
|
|
1 x 1 x |
|
−3 −2 −1 |
|
|
|
|
1 2 |
3 |
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
′( ) = |
|
4 |
|
1 |
− |
|
= |
4 |
( −1 |
)( + ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
f |
|
x |
|
|
|
|
|
x2 2 |
|
|
|
|
x2 2 |
|
, |
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
6.22. Damit sind x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
siehe Beispiel |
|
|
1 die einzigen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
( |
|
+ ) |
|
|
( |
+ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f einen Extremwert |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Stellen, an denen die Funktion |
|
= ± |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
haben kann. |
|
|
|
|
|
1 wechselt f′ das Vorzeichen von minus nach plus. Es liegt an dieser Stelle |
||||||||||||||||||||||||||||||||||||||||
An der Stelle x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
also ein |
Minimum vor. Für x |
|
1 wechselt f |
′ |
das Vorzeichen von plus nach minus. Somit hat f |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= − |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
|||||||
für x |
= |
1 ein Maximum. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Beispiel 6.25 zeigt einen typischen Sachverhalt. Der Nachweis eines Extremwertes mithilfe der zweiten Ableitung kann zu umfangreichen Berechnungen führen. Oft führen andere Überlegungen schneller zum Ziel.
Nachweis eines Extremums
Der Nachweis eines Extremums durch das Vorzeichen der zweiten Ableitung ist in manchen Fällen sehr aufwendig. Oftmals ist es einfacher, die erste Ableitung bezüglich eines Vorzeichenwechsels zu untersuchen oder den Nachweis durch Grenzwertbetrachtungen zu führen. Der Test auf einen Vorzeichenwechsel hat außerdem den Vorteil, dass auch anstellen, an denen die zweite Ableitung null ist, entschieden werden kann, ob ein Extremum vorliegt oder nicht.
Sondersituationen treten am Rand des Definitionsbereichs auf. Bei der Suche nach Extrema sind die Funktionswerte am Rand unbedingt zu berücksichtigen.
Beispiel 6.27 (Extrema am Rand)
Um die Extremwerte der Funktion |
|
y |
|||||
f x |
√1 x2 |
|
|
1 f(x) = √1 − x2 |
|||
zu bestimmen,( ) = betrachten− |
wir die erste Ableitung |
|
|
||||
f′ |
x |
2 |
2 x |
x |
|
|
|
−1 x2 |
1− x2 . |
|
|
||||
|
( ) = |
√ |
|
= √ |
|
|
|
Lediglich an der |
Stelle x 0 ist die erste Ableitung |
|
|
||||
|
− |
− |
|
|
|||
null. An dieser Stelle hat f=′ einen Vorzeichenwechsel |
−1 |
1 x |
|||||
von plus nach minus. Somit handelt es sich um ein
lokales Maximum. |
|
|
|
|
|
1 und x |
|
1. An diesen beiden |
|||
Der Definitionsbereich der Funktion erstreckt sich zwischen x |
|
|
|||||||||
Randstellen hat die Funktion den Wert null: |
f 1 |
|
1 |
|
1 |
2 |
|
0 |
. In |
der Umgebung dieser |
|
(± ) = |
|
|
|
= − |
|
= |
|
||||
|
|
|
− (± ) = |
|
|
|
|
||||
|
|
liegen laut Definition 6.10 an den Stellen |
|||||||||
beiden Stellen sind alle Funktionswerte positiv. Somit » |
|
|
|
|
|
|
|
Ì |
|||
x = ±1 lokale Minima vor. |
|
|
|
|
|
|
|
|
|
|
|
