102 |
3 Vektoren |
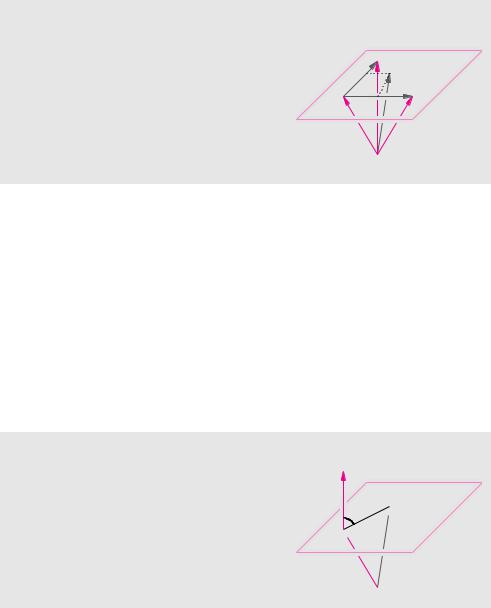
Eine Ebene lässt sich auch dadurch festlegen, dass man drei Punkte vorgibt. Diese drei Punkte müssen allerdings auch zwei linear unabhängige Richtungsvektoren definieren. Das erreicht man durch die Forderung, dass nicht alle drei Punkte auf einer Geraden liegen.
Definition 3.22 (Dreipunkteform einer Ebene)
Eine Ebene E kann durch drei Punkte P0, P1 und P2, die nicht alle auf einer Geraden liegen, mit den Ortsvektoren x0, x1 und x2 festgelegt werden:
E x = x0 + λ (x1 − x0) + µ (x2 − x0) ,
λ, µ R.
Die Parameter λ und µ sind unabhängig voneinander.
E
|
|
|
P2 |
|
|
|
2 |
|
|
P |
|
|
|
|
|
||
P0 |
x |
|
|
P1 |
|
x |
x |
|
|||
|
0 |
x |
1 |
||
|
|
|
|
|
|
|
|
|
|
O |
|
3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
Bei der parameterfreien Darstellung werden Geraden und Ebenen durch Gleichungen dargestellt. Wir werden sehen, dass man eine Ebene sehr elegant durch eine einzige Gleichung beschreiben kann. Die Ebene besteht aus allen Punkten, die diese Gleichung erfüllen. Die entscheidende Idee ist die Festlegung der Ebenenrichtung durch einen Normalenvektor n. Ein Normalenvektor steht senkrecht auf allen Vektoren, die in der Ebene liegen. Bei einem Normalenvektor ist lediglich die Richtung festgelegt. Die Länge und die Orientierung des Normalenvektors sind durch die Ebene nicht eindeutig festgelegt. Wenn x0 der Ortsvektor eines festen Punktes P0 in der Ebene E ist, dann muss der Ortsvektor x eines beliebigen Punktes P in der Ebene die Gleichung (x − x0) n = 0 erfüllen. Vektoren stehen ja gerade dann senkrecht aufeinander, wenn das Skalarprodukt null ist.
Definition 3.23 (Parameterfreie Darstellung einer Ebene)
Eine Ebene E durch den Punkt P0 mit dem Ortsvektor x0 und dem Normalenvektor n ≠ 0 kann man in Form einer Gleichung darstellen:
E (x − x0) n = 0.
Ein Punkt P mit dem Ortsvektor x liegt genau dann in der Ebene, wenn die Gleichung erfüllt ist.
n
P0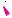
x
0
P
x
O
E
3.4 Punkte, Geraden und Ebenen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
||||||||||
In der Koordinatendarstellung mit P |
0( |
x |
0 S |
y |
0 S |
z |
0) |
und P |
( |
x |
S |
y |
S |
z |
) |
lautet die Gleichung aus |
||||||||||||||
Definition 3.23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x |
|
x0 |
|
nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
’ |
y |
− y0 |
“ ’ |
ny |
“ |
0 |
|
|
|
|
nx x ny y nz z nx x0 ny y0 nz z0 . |
||||||||||||||||||
|
z |
− |
z |
0 |
n |
z |
|
Ô |
|
|
|
|
+ |
+ |
|
|
|
= |
|
|
+ |
d |
+ |
|
||||||
|
– |
|
|
— – |
|
— = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Wenn |
” |
|
− |
|
|
• ” |
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|||||
|
der Normalenvektor n ein Einheitsvektor ist, dann kann man durch einfache geome- |
|||||||||||||||||||||||||||||
trische Überlegungen zeigen, dass der Betrag von d den Abstand der Ebene vom Ursprung angibt. In diesem Fall spricht man von der Hesseschen Normalenform einer Ebene. Die Bezeichnung geht auf den Mathematiker Luwig Otto Hesse zurück.
Definition 3.24 (Hessesche Normalenform)
Bei der parameterfreien Darstellung einer Ebene
E nxx + nyy + nzz = d
sind die Faktoren nx, ny und nz die Koordinaten des Normalenvektors n ≠ 0. Falls der Normalenvektor n ein Einheitsvektor ist, bezeichnet man die Darstellung als Hessesche Normalenform.
Die Umrechnung zwischen parameterbehafteter und parameterfreier Darstellung einer Ebene ist einfach. Sie basiert auf der Eigenschaft, dass der Normalenvektor senkrecht auf allen Vektoren der Ebene steht.
Darstellung einer Ebene mit und ohne Parameter
Die Umrechnung zwischen einer Parameterdarstellung und einer parameterfreien Darstellung einer Ebene
E x = x0 + λ a + µ b (x − x0) n = 0
erfolgt mittels der Beziehung n = a × b.
Auch Geraden kann man durch Gleichungen, also parameterfrei, darstellen. Allerdings benötigt man für eine Gerade im Raum zwei Gleichungen. Jede einzelne Gleichung repräsentiert dabei eine Ebene. Die Gerade ist als Schnittgerade dieser beiden Ebenen festgelegt. Wir gehen hier jedoch nicht auf weitere Details ein.
3.4.4 Schnitte von Geraden und Ebenen
Schnitte von Geraden und Ebenen lassen sich immer durch Lösen entsprechender linearer Gleichungssysteme bestimmen. Allerdings kann man dabei mehr oder weniger geschickt vorgehen. Wir betrachten zunächst die Schnitte zweier Geraden. Dabei werden zwei Geraden als windschief bezeichnet, falls sie weder parallel verlaufen noch einen Schnittpunkt besitzen.
104 |
3 Vektoren |
Schnitt zweier Geraden
Die Schnittpunkte zweier Geraden g1 und g2 in Parameterdarstellung bestimmt man aus dem linearen Gleichungssystem
g1 |
|
x |
x1 |
+ |
λ1 a1 |
|
g1 |
|
g2 |
|
x1 |
|
λ1 a1 |
|
x2 |
|
λ2 a2 |
g2 |
x |
= x2 |
λ2 a2 |
¡ Ô |
∩ |
|
+ |
= |
+ |
||||||||
|
|
|
= |
+ |
|
|
|
|
|
|
|
mit den beiden Unbekannten λ und µ. Falls das Gleichungssystem
Lgenau eine Lösung hat, dann besitzen die beiden Geraden einen Schnittpunkt,
Lunendlich viele Lösungen hat, dann sind die beiden Geraden identisch,
Lkeine Lösung hat, dann sind die Geraden parallel oder windschief.
Beispiel 3.21 (Schnitt zweier Geraden)
Wir betrachten die beiden Geraden
g1 |
|
x |
|
1 |
“ |
λ1 |
|
2 |
“ |
, |
g2 |
|
x |
’ |
5 |
“ |
λ2 |
|
8 |
“ . |
|
’ −3 |
’ −3 |
|
2 |
’ −4 |
|||||||||||||||
|
|
= – |
1 |
— + |
|
– |
1 |
— |
|
|
|
= – −3 |
— + |
|
– |
2 |
— |
|||
|
|
|
” |
− |
• |
|
” |
|
• |
|
|
|
|
” − |
|
• |
|
” |
|
• |
Wir untersuchen nun, ob g1 und g2 gemeinsame Punkte haben. Dazu setzen wir die beiden Darstellungen für x gleich und erhalten das überbestimmte lineare Gleichungssystem
2 λ |
+ |
8 µ |
= |
6 |
←Ð |
|
λ |
− |
2 µ |
|
2 |
||||
−3 λ |
4 µ |
5 |
Ô |
4 µ |
= −2 |
||||||||||
λ |
− |
2 µ |
= −2 |
S ( |
2 |
←Ð3 |
|
2 µ |
= |
1 |
|||||
|
− |
|
= − |
|
|
) S (− ) |
|
1 und µ |
1 |
|
= |
|
|||
Das Gleichungssystem hat die eindeutige Lösung λ |
= − |
= 2 |
. Damit erhalten wir als |
||||||||||||
Schnittpunkt den Punkt S 1 |
0 |
S − |
2 . |
|
|
|
Ì |
||||||||
|
|
|
( |
S |
|
) |
|
|
|
|
|
|
|||
Wir kommen nun zum Schnitt einer Geraden mit einer Ebene. Die Ebene kann dabei in Parameterdarstellung oder auch als parameterfreie Gleichung definiert sein.
Schnitt einer Geraden mit einer Ebene
Die Schnittpunkte einer Geraden g mit einer Ebene E bestimmt man, indem man
Leine Parameterdarstellung der Geraden g und eine Parameterdarstellung der Ebene E gleichsetzt oder
Leine Parameterdarstellung der Geraden g in eine parameterfreie Gleichung der Ebene E einsetzt.
Im Zweifelsfall ist die zweite Methode zu empfehlen. Durch Einsetzen einer Parameterdarstellung der Geraden in eine Gleichung der Ebene entsteht nur eine einzige Gleichung mit einer Unbekannten, siehe Beispiel 3.22.
3.4 Punkte, Geraden und Ebenen |
105 |
Beispiel 3.22 (Schnitt einer Geraden mit einer Ebene)
Zur Berechnung des Schnittpunktes zwischen der Geraden g und der Ebene E
g |
|
x |
’ |
0 |
“ |
λ |
’ |
1 |
“ |
, |
E |
|
5x |
+ |
2y |
+ |
4z |
− |
6 |
= |
0 |
2 |
2 |
||||||||||||||||||||
|
|
= – |
2 |
— + |
|
– −1 |
— |
|
|
|
|
|
|
|
|||||||
|
|
|
” − |
|
• |
|
” |
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
setzt man die Koordinaten der Geraden in die Ebenengleichung ein:
5(0 + λ) + 2(2 − 2λ) + 4(−2 + λ) − 6 = 0 Ô 5λ = 10 Ô λ = 2.
Durch Einsetzen dieses Parameterwertes λ in die Geradengleichung erhält man den Schnittpunkt S(2 S − 2 S 0). Als Probe der Rechnung kann man den Schnittpunkt S schließlich in die Ebenen-
gleichung einsetzen. |
Ì |
Schnitt zweier Ebenen
Die Schnittpunkte zweier Ebenen E1 und E2 bestimmt man, indem man
Ldie Parameterdarstellungen der beiden Ebenen gleichsetzt oder
Ldas Gleichungssystem aus den beiden Ebenengleichungen löst oder
Leine Parameterdarstellung einer Ebene in eine parameterfreie Gleichung der anderen Ebene einsetzt.
Beispiel 3.23 (Schnitt zweier Ebenen)
Zur Untersuchung der Schnittpunkte der beiden Ebenen
E1 x − 2y + 4z + 2 = 0 |
E2 2x − 3y + z − 5 = 0 |
stellen wir das folgende unterbestimmte lineare Gleichungssystem auf:
x |
− |
2 y |
+ |
4 z |
= |
2 |
2 |
|
x |
− |
y |
+ |
4 z |
= |
2 |
2 x |
3 y |
z |
−5 |
S (− ) |
Ô |
|
2 y |
7 z |
−9 |
||||||
|
− |
|
+ |
|
= |
|
←Ð |
|
|
|
− |
|
= |
|
Aus der freien Variablen z = λ folgt y = 9 + 7λ und daraus schließlich x = 16 + 10λ. Wir erhalten als Lösung die Schnittgerade
g |
|
x |
’ |
16 |
“ |
λ |
’ |
10 |
“ . |
|
9 |
7 |
|
||||||||
|
|
= – |
0 |
— + |
|
– |
1 |
— |
Ì |
|
|
|
|
” |
|
• |
|
” |
|
• |
3.4.5 Abstände
Abstände zwischen Elementen spielen in der Geometrie eine wichtige Rolle. In der Computergrafik etwa kann man mithilfe der Abstände von Objekten zur Bildebene feststellen, welche Objekte bezüglich der Bildebene weiter hinten und damit eventuell verdeckt, und welche weiter vorn, also frei sichtbar, liegen. Typischerweise wird das Bild von hinten
106 |
3 Vektoren |
nach vorn aufgebaut. Diese Vorgehensweise bezeichnet man auch in Anlehnung an den Bildaufbau eines Gemäldes als Painter’s Algorithmus.
Satz 3.17 (Abstand eines Punktes zu einer Geraden)
Der Abstand des Punktes P mit dem Ortsvek-
tor xP zur Geraden g |
|
|
|
|
|
|
a |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
x |
x0 |
|
λa |
|
|
|
|
|
|
|
|||
ist die Entfernung= |
+zwischen dem Punkt P und |
|||||||||||||
seinem Lotfußpunkt: |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
xP |
x0 |
|
a |
|
|
|
dP |
= W |
xP |
− Œ |
x0 |
+ |
( |
|
− |
) |
|
a |
‘W |
. |
|
|
|
|
|
|
|
a a |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0
`
O
xP
L |
g |
|
|
|
d |
|
P |
|
P |
Zur Herleitung einer Formel für den Abstand eines Punktes P mit dem Ortsvektor xP zu einer Geraden führt man den Lotfußpunkt L mit dem Ortsvektor ` ein:
g x = x0 + λa, |
` = x0 + λL a. |
Der Lotvektor LP = xP − ` steht senkrecht auf der Geraden. Daraus erhalten wir
|
( |
|
− |
|
) = |
0 |
Ô |
|
|
|
= |
|
( |
|
+ |
|
) Ô |
|
= |
( |
xP |
− |
x0 |
) |
a |
a |
xP |
` |
a |
xP |
a |
x0 |
λLa |
λL |
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a a |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Bei diesen Umformungen haben wir die Rechenregeln für das Skalarprodukt, siehe Satz 3.3, eingesetzt. Der Abstand ist dann die Entfernung von P zu L, also dP = SxP − `S.
Beispiel 3.24 (Abstand Punkt zu Gerade)
Zur Berechnung des Abstands des Punktes P (3 S 2 S 1) zu der Geraden g mit folgender Parameterdarstellung berechnet man zunächst den Parameterwert λL des Lotfußpunktes L:
|
|
|
|
|
|
|
|
|
’ |
2 |
“ ’ |
1 |
“ |
|
|
|
g |
x |
|
1 |
λ |
1 |
|
λL |
|
4 |
1 |
|
1. |
||||
’ |
2 |
1 |
“ |
|
– |
2 |
— – −0 |
— |
|
|||||||
|
|
3 |
“ ’ |
0 |
|
|
” |
−1 |
• ” |
1 |
• |
|
|
|||
|
|
= – − |
|
— + – − |
|
— Ô |
|
= |
|
|
|
|
|
|
= − |
|
|
|
|
|
’ |
1 |
“ ’ |
1 |
“ |
|
|||||||
|
|
” |
|
• ” |
|
• |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
– −0 |
— – −0 |
— |
|
|
|||
|
|
|
|
|
|
|
|
|
” |
|
• ” |
|
• |
|
|
|
Für den Ortsvektor ` des Lotfußpunktes und den Abstand gilt demnach
|
’ |
1 |
“ |
|
’ |
1 |
“ ’ |
0 |
“ |
` |
2 |
1 |
1 |
1 |
|||||
|
= – −3 |
— + (− |
|
) – −0 |
— = – −3 |
— Ô |
|||
|
” |
|
• |
|
” |
|
• ” |
|
• |
dP |
R |
2 |
|
|
1 |
R |
|
22. |
|
||
|
R |
3 |
|
|
0 |
R |
|
|
|
|
|
|
R’ |
|
“ |
’ |
|
“R |
|
|
|
|
Ì |
|
R |
1 |
|
|
3 |
R |
|
√ |
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
R |
|
— − – − |
|
R |
= |
|
|
|
|
|
|
= R– |
|
|
—R |
|
|
|
|
|||
|
R |
|
|
|
|
R |
|
|
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
R |
|
• |
” |
|
R |
|
|
|
|
|
|
R” |
|
|
•R |
|
|
|
|
|
||
|
R |
|
|
|
|
R |
|
|
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
Der Abstand eines Punktes zu einer Ebene lässt sich sehr einfach bestimmen, wenn man die Hessesche Normalenform der Ebene kennt. Man muss lediglich die Koordinaten des Punktes in die Ebenengleichung einsetzen.
3.4 Punkte, Geraden und Ebenen |
107 |
Satz 3.18 (Abstand eines Punktes zu einer Ebene)
Mit der Hesseschen Normalenform einer Ebene
Enxx + nyy + nzz + d = 0,
»
n2x + n2y + n2z = 1
berechnet man den Abstand eines Punktes P mit dem Ortsvektor xP zur Ebene E durch Einsetzen von P in die Ebenengleichung:
dP = TnxxP + nyyP + nzzP + dT.
P0
P E
dP
L |
x |
P |
|
` |
|
x 0
O
In der Hesseschen Normalenform hat der Normalenvektor n die Länge 1. Für den Lotvektor LP vom Lotfußpunkt L zum Punkt P gelten die beiden Beziehungen
LP = xP − ` = (xP − x0) + (x0 − `), LP = rn.
Dabei ist r ein Skalierungsfaktor. Durch Gleichsetzen und anschließender Skalarmultiplikation mit n ergibt sich, bis auf das Vorzeichen, der gesuchte Abstand
dP = SrS = S(xP − x0) nS.
Anhand des Vorzeichens von r kann man erkennen, auf welcher Seite der Ebene der Punkt P liegt.
Beispiel 3.25 (Abstand Punkt zu Ebene)
Den Abstand des Punktes P (1 S −2 S 4) zur Ebene E mit der Gleichung bzw. Hesseschen Normalenform
−2 x + 2y − z + 4
E −2 x + 2y − z + 4 = 0 Ô √ = 0 9
berechnet man kurz und bündig aus der Formel
dP = V −2 1 + 2 (−2) − 4 + 4 V = 2. Ì
3
Satz 3.19 (Abstand zweier windschiefer Geraden)
Den Abstand der beiden windschiefen Geraden |
|
|
a |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
2 |
|
|
g1 |
x |
x1 |
λ1a1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
g2 |
x |
= x2 |
+ λ2a2 |
|
|
|
|
L2 |
g2 |
||||
kann man |
durch folgende Formel berechnen: |
O |
|
d |
|
||||||||
|
= |
|
+ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
− |
|
1)S. |
x |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
d |
|
|
|
a |
x |
x |
|
a1 |
L1 |
|
|||
|
S(a1 × |
a21) (a22 |
|
|
|
||||||||
|
= |
|
S |
|
× S |
|
|
|
|
|
|
|
|
g1