
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

3.3 Vektoren in Koordinatendarstellung |
89 |
Für die Komponentenzerlegung im Raum benötigt man drei linear unabhängige Vektoren.
Definition 3.14 (Komponentenzerlegung im Raum)
Falls die drei Vektoren a1, a2 und a3 linear unabhängig sind, nennt man
b = λ1a1 + λ2a2 + λ3a3
die Komponentenzerlegung des Vektors b in Richtung der Vektoren a1, a2 und a3. Für die Koe zienten λ1, λ2 und λ3 gilt:
|
|
b, a , a |
|
a , b, a |
|
|
a , a , b |
||||||
λ1 |
= |
[a1 |
, a22 |
, a33] |
, λ2 |
= |
[a11, a2 |
, a33] |
, λ3 |
= |
[a11, a22, a3] |
. |
|
|
[ |
|
] |
[ |
] |
[ |
] |
||||||
Wir müssen noch klären, wie die Berechnungsformeln der Koe zienten λ1, λ2 und λ3 in Definition 3.14 zu rechtfertigen sind. Dazu multiplizieren wir die Komponentenzerlegung des Vektors b mit dem Vektor a2 × a3:
b |
a a |
λ |
1 |
a |
a2 |
a3 |
) + |
λ2 a2 |
a2 |
× |
a3 |
) + |
λ3 a3 |
a2 |
× |
a3 |
) |
. |
|
|
b(, a22 |
,×a33) = |
|
|
1a1(, a2 |
,×a3 |
|
( 0 |
|
|
( 0 |
|
|
||||||
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|||||||||||||
[ |
] |
|
|
[ |
] |
|
|
|
|
|
|
|
|
|
|
|
|
||
Da der Vektor a2 × a3 sowohl auf dem Vektor a2 als auch auf dem Vektor a3 senkrecht steht, ergeben die jeweiligen Skalarprodukte null. Dadurch erhalten wir
[b, a2, a3] = λ1 [a1, a2, a3] .
Unter der Voraussetzung, dass die drei Vektoren a1, a2 und a3 linear unabhängig sind, ist das Spatprodukt dieser Vektoren nicht null und wir können die Gleichung nach λ1 auflösen. Auf dieselbe Art erfolgt die Berechnung von λ2 und λ3. Diese Berechnungsmethode ist unter dem Namen Cramersche Regel zum Lösen linearer Gleichungssysteme bekannt, siehe
Satz 4.4.
3.3 Vektoren in Koordinatendarstellung
Laut Definition 3.1 sind Vektoren mathematische Objekte, die eine bestimmte Richtung und eine bestimmte Länge besitzen. Diese Definition ist zwar geometrisch anschaulich, allerdings erfordert es einigen Aufwand, geometrisch definierte Berechnungen, wie etwa das Skalarprodukt, das Kreuzprodukt oder das Spatprodukt, mit Computerprogrammen zu realisieren. Deshalb wählen wir in diesem Abschnitt einen neuen Ansatz. Wir beschreiben Vektoren durch Koordinaten und klären, wie man die Berechnungen mithilfe dieser Koordinaten durchführen kann.

90 |
3 Vektoren |
3.3.1 Koordinatendarstellung
Die Koordinatendarstellung von Vektoren beruht auf Basisvektoren. In der Mathematik gibt es verschiedene Möglichkeiten, Basisvektoren sinnvoll festzulegen. Wir arbeiten in diesem Abschnitt mit Basisvektoren, die jeweils die Länge 1 haben, paarweise senkrecht zueinander stehen und ein Rechtssystem bilden. Für Vektoren in der Ebene genügen zwei Basisvektoren, für Vektoren im Raum benötigen wir drei Basisvektoren. Auch wenn es anschaulich schwerfällt, wir könnten auch n Basisvektoren in einem n-dimensionalen Raum betrachten. Im Abschnitt 3.4 werden wir im Zusammenhang mit Punkten, Geraden und Ebenen noch speziell auf das kartesische Koordinatensystem eingehen.
Definition 3.15 (Basisvektoren und Koordinaten)
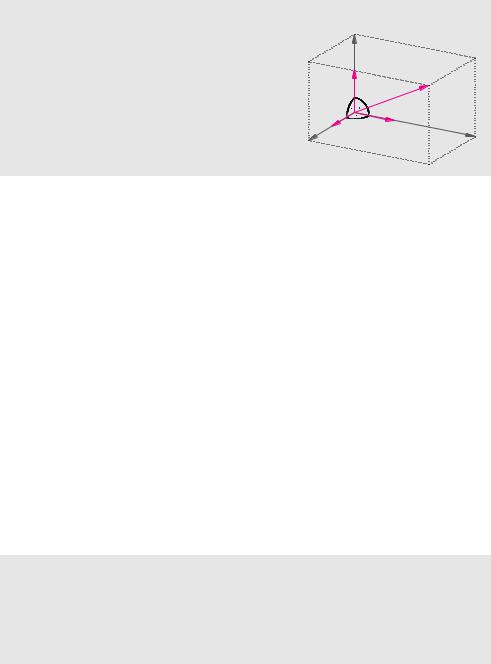
Drei Einheitsvektoren e1, e2 und e3, die paarweise senkrecht aufeinander stehen und in dieser Reihenfolge ein Rechtssystem bilden, bezeichnet man als Basisvektoren. Jeder Vektor a lässt sich durch
a = a1 e1 + a2 e2 + a3 e3
darstellen. Dabei nennt man die Skalare a1, a2 und a3 die Koordinaten und die Vektoren a1 e1, a2 e2 und a3 e3 die Komponenten des Vektors a.
e3
e1
e2
Vektoren in einer Ebene stellen immer einen Spezialfall von Vektoren im Raum dar. Ebene Vektoren können wir durch räumliche Vektoren beschreiben, in dem wir beispielsweise die dritte Koordinate null setzen.
Üblicherweise fasst man die Koordinaten a1, a2 und a3 eines Vektors a in einer einzigen Spalte zusammen:
a a1 e1 a2 e2 a3 e3 a1 ’ |
1 |
“ |
a2 ’ |
0 |
“ |
a3 ’ |
0 |
“ ’ |
a1 |
“ . |
|||
0 |
1 |
0 |
a2 |
||||||||||
= |
+ |
+ |
= – |
0 |
— |
+ – |
0 |
— |
+ – |
1 |
— = – |
a |
— |
3 |
|||||||||||||
|
|
|
” e1 |
• |
” e2 |
• |
” e3 |
• ” |
|
• |
|||
|
|
|
´¹¹¹¹¹¹¸¹¹¹¹¹¶ |
´¹¹¹¹¹¹¸¹¹¹¹¹¶ |
´¹¹¹¹¹¹¸¹¹¹¹¹¶ |
|
|
||||||
Die Basisvektoren stehen paarweise senkrecht. Damit lässt sich die Länge eines Vektors nach dem Satz von Pythagoras in rechtwinkligen Dreiecken berechnen, siehe Satz 1.6. Der Betrag ist sowohl für Vektoren in der Ebene als auch Vektoren im Raum berechenbar.
3.3 Vektoren in Koordinatendarstellung |
91 |
Satz 3.10 (Betrag von Vektoren in Koordinaten)
Für den Betrag eines Vektors a gilt: |
|
3 |
||||||||||||
|
|
R |
|
|
R |
¼ |
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
3 |
|||
|
|
a1 |
|
|
|
|
|
|
|
a |
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
R’ |
a |
3 |
“R |
|
|
|
|
|
|
|
|
|
|
|
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
|
|
a |
R |
a |
|
R |
|
a2 |
|
a2 |
|
a2. |
|
3 |
|
S |
|
S = R– |
|
|
—R = |
|
|
+ |
|
+ |
|
|
|
1 |
|
|
R |
|
2 |
R |
1 |
|
2 |
|
3 |
|
|
||
|
|
R |
|
R |
|
|
|
|
e |
|||||
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
e |
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
1 |
|
|
R” |
|
|
•R |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|
|
|
|
|
|
|
|
e |
|
|
R |
|
|
R |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a
e |
|
|
2 |
a |
|
|
2 e |
|
|
|
2 |
Beispiel 3.8 (Länge eines Vektors)
Wie muss man die Koordinate a3 des Vektors
’ 1 “ a = – 2 — ” a3 •
wählen, damit der Vektor die Länge 3 hat? Für die Länge gilt
|
|
|
|
a |
|
|
» |
|
|
|
|
|
|
|
3 |
|
5 |
|
a32 |
|
9 |
|
a32 |
|
4. |
|
|
|
S |
S = |
12 |
+ |
22 |
+ |
a32 |
= |
Ô |
+ |
= |
Ô |
= |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Für |
a |
3 |
= ± |
2 |
hat der Vektor |
a |
somit die Länge |
3 |
. |
|
|
|
Ì |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
3.3.2 Addition und Subtraktion
Formeln für die Addition und Subtraktion von Vektoren in Koordinaten erhalten wir mithilfe der Rechenregeln aus Satz 3.1:
a ± b = Ša1 e1 + a2 e2 + a3 e3• ± Šb1 e1 + b2 e2 + b3 e3•
=(a1 ± b1) e1 + (a2 ± b2) e2 + (a3 ± b3) e3.
Die Koordinaten von Vektoren dürfen also, wie erwartet, einfach addiert oder subtrahiert werden.
Satz 3.11 (Addition und Subtraktion von Vektoren in Koordinaten)
Für die Addition und Subtraktion der Vektoren a und b gilt:
|
|
a1 |
|
|
b1 |
|
|
a1 |
|
b1 |
|
|||
a b |
’ |
a2 |
“ |
’ |
b2 |
“ |
’ |
a2 |
± b2 . |
|||||
|
a |
3 |
b |
3 |
a |
± |
b |
3 |
“ |
|||||
± = – |
|
— ± – |
|
— = – |
3 |
|
— |
|||||||
|
” |
|
|
• |
” |
|
|
• |
” |
|
± |
|
|
• |

92 |
3 Vektoren |
3.3.3 Skalare Multiplikation
Die Multiplikation des Vektors a mit dem Skalar λ erfolgt durch
λ a = λ (a1 e1 + a2 e2 + a3 e3) = (λ a1)e1 + (λ a2)e2 + (λ a3)e3.
Jede einzelne Koordinate wird also mit dem Faktor λ multipliziert.
Satz 3.12 (Skalare Multiplikation von Vektoren in Koordinaten)
Für die skalare Multiplikation des Vektors a mit dem Skalar λ gilt:
λ a λ ’ |
a1 |
“ ’ |
λ a1 |
“ . |
a2 |
λ a2 |
|||
= – |
a |
— = – |
λ a |
— |
3 |
3 |
|||
” |
|
• ” |
|
• |
Beispiel 3.9 (Einheitsvektoren)
Zu den Vektoren
a |
’ |
1 |
“ |
, |
b |
’ |
1 |
“ |
, |
c |
’ |
1 |
“ |
1 |
1 |
2 |
|||||||||||
|
= – |
0 |
— |
|
|
= – |
1 |
— |
|
|
= – −3 |
— |
|
|
” |
|
• |
|
|
” |
|
• |
|
|
” |
|
• |
sollen die jeweiligen Einheitsvektoren bestimmt werden. Dazu multiplizieren wir jeden Vektor mit dem Kehrwert der jeweiligen Länge:
ea |
|
|
2 ’ |
1 |
“ , eb |
|
|
3 ’ |
1 |
“ , ec |
|
|
14 ’ |
1 |
“ . |
|
|||
|
|
1 |
|
|
1 |
|
|
2 |
|
||||||||||
|
1 |
– |
|
— |
1 |
– |
|
— |
1 |
– |
−3 |
— |
|
||||||
|
= |
√ |
|
0 |
= |
√ |
|
1 |
= |
√ |
|
Ì |
|||||||
|
|
|
|
||||||||||||||||
|
|
|
|
” |
|
• |
|
|
|
” |
|
• |
|
|
|
” |
|
• |
|
3.3.4 Skalarprodukt
Entscheidend für das Skalarprodukt zweier Vektoren sind die Skalarprodukte der Basisvektoren. Das Skalarprodukt von zwei Vektoren ist definiert als das Produkt der beiden Längen der Vektoren multipliziert mit dem Kosinus des eingeschlossenen Winkels, siehe Definition 3.7. Zwei verschiedene Basisvektoren stehen immer senkrecht zueinander, dadurch ist ihr Skalarprodukt null. Beim Skalarprodukt eines Basisvektors mit sich selbst sind die beiden Längen jeweils 1 und der Winkel ist 0○. Dadurch ergibt dieses Skalarprodukt immer 1. Insgesamt erhalten wir
a |
|
b |
|
a1 e1 |
+ |
a2 e2 |
+ |
a3 e3 |
) ( |
b1 e1 |
+ |
b2 e2 |
+ |
b3 e3 |
) |
|||||||
|
|
= (1 |
1 |
|
e1 |
|
|
e2 |
|
|
|
e3 |
||||||||||
|
|
|
= |
a b |
|
e1 |
|
+ |
a1 b2 e1 |
|
+ |
a1 b3 e1 |
|
|||||||||
|
|
|
a b |
|
e2 |
1e1 |
a2 b2 |
e2 |
0e2 |
a2 b3 |
e2 |
0e3 |
|
|||||||||
|
|
|
+ |
2 |
1 |
² |
+ |
a3 b2 |
² |
+ |
a3 b3 |
² |
|
|||||||||
|
|
|
a b |
|
e3 |
0e1 |
e3 |
1e2 |
e3 |
0e3 . |
||||||||||||
|
|
|
+ |
3 |
1 |
² |
+ |
|
² |
+ |
|
² |
|
|||||||||
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
² |
|
|
|
² |
|
|
|
² |
|
|||||||

3.3 Vektoren in Koordinatendarstellung |
93 |
Beim Skalarprodukt müssen wir also lediglich sich entsprechende Koordinaten multiplizieren und dann diese Produkte addieren.
Satz 3.13 (Skalarprodukt von Vektoren in Koordinaten)
Für das Skalarprodukt der Vektoren a und b gilt:
a b |
’ |
a1 |
“ ’ |
b1 |
“ |
|
a1b1 a2b2 a3b3. |
||||
a2 |
b2 |
|
|||||||||
|
= – |
a |
— – |
b |
— = |
|
+ |
+ |
|||
|
3 |
3 |
|
||||||||
|
|
” |
|
• ” |
|
• |
|
|
|
|
|
Beispiel 3.10 (Orthogonale Vektoren) |
|
|
|||||||||
Gegeben sind die beiden Vektoren |
|
|
|
||||||||
a |
’ |
2 |
“ , |
b |
|
’ |
1 |
“ . |
|
|
|
1 |
|
b2 |
|
|
|||||||
|
= – −2 |
— |
|
= – |
2 |
— |
|
|
|
||
|
” |
|
• |
|
|
” |
|
• |
|
|
|
Für welche Werte der Koordinate b2 stehen die beiden Vektoren senkrecht und für welche Werte ist der Winkel zwischen den beiden Vektoren größer als 90○? Die beiden Vektoren a und b stehen senkrecht, falls das Skalarprodukt null ergibt:
Für |
b |
2 |
a6 b = 2 1 − 1 b2 + 2 2 = 0 Ô b2 = 6. |
90 |
○. |
Ì |
|||||||||
|
> |
wird das Skalarprodukt negativ und der eingeschlossene Winkel größer als |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Beispiel 3.11 (Skalarprodukt, Winkel und Projektion) |
|
|
|
||||||||||||
Gegeben sind die Vektoren |
|
|
|
|
|
|
|||||||||
|
|
|
a |
’ |
|
1 |
“ , |
b |
= |
’ |
2 |
“ . |
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|||||||
|
|
|
|
= – |
− |
1 |
— |
|
– |
1 |
— |
|
|
|
|
|
|
|
|
” |
|
• |
|
|
” |
|
• |
|
|
|
|
Aus den Koordinaten lässt sich das Skalarprodukt der beiden Vektoren berechnen:
a b = 1 2 + 2 1 + (−1) 1 = 3.
Mit dem Skalarprodukt berechnen wir den Winkel α zwischen den beiden Vektoren:
cos α |
|
|
a |
|
b |
|
|
|
3 |
|
|
1 |
|
|
|
π |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
. |
|||
= |
|
a |
b |
= √ |
|
|
|
|
= |
2 |
Ô |
= |
3 |
||||||
|
6 |
6 |
|||||||||||||||||
|
S S S S |
|
√ |
|
|
|
|
|
|||||||||||
Die senkrechte Projektion des Vektors b in Richtung des Vektors a liefert Definition 3.8:
ba |
a |
|
2 a |
|
|
6 2 ’ |
1 |
“ |
2 ’ |
1 |
“ . |
|
|||||||
|
|
|
2 |
2 |
|
||||||||||||||
a |
|
b |
|
|
3 |
|
– |
|
— = |
1 |
– |
|
— |
|
|||||
= |
S |
|
|
= |
|
√ |
|
|
1 |
|
|
1 |
Ì |
||||||
|
|
|
|
||||||||||||||||
|
|
|
S |
|
( |
) |
” − |
|
• |
|
|
” − |
|
• |
|
||||
Skalarprodukte ermöglichen die Berechnung von Winkeln. Insbesondere können wir damit die Winkel, die ein Vektor a mit den Basisvektoren einschließt, berechnen:
cos |
( |
|
) = |
a |
|
e1 |
= |
a1 |
|||
a, e1 |
S |
a |
e1 |
S |
|
. |
|||||
a |
|||||||||||
|
|
|
S S |
|
S S |
||||||
