
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

188 |
5 Funktionen |
5.3.2 Periode
Unter einer periodischen Funktion versteht man eine Funktion, die sich im Abstand von einem festen Wert immer wiederholt. Die bekanntesten periodischen Funktionen sind Sinus und Kosinus, siehe Abschnitt 5.4.
Definition 5.21 (Periodische Funktion)
Eine Funktion f ist periodisch mit der Periode p > 0, wenn
f(x + p) = f(x)
für alle reellen Zahlen x.
Die Forderung, dass die Gleichung f(x + p) = f(x) für alle reellen Zahlen x erfüllt ist, ist streng genommen zu restriktiv. Es gibt auch periodische Funktionen, die Definitionslücken haben, beispielsweise der Tangens. Konstante Funktionen sind auch periodisch. Allerdings ist es nicht sinnvoll, von einer kleinsten Periode zu sprechen.
Beispiel 5.41 (Periodische Funktion)
Die Funktion
f(x) = SxS für x [−1, 1], f(x + 2) = f(x)
ist periodisch. Die kleinste Periode ist p = 2. Der über dem Intervall [−1, 1] definierte Funktionsprototyp wird zu einer Funktion fortgesetzt, die für alle reellen Zahlen definiert ist.
|
|
y |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
1 |
|
|
|
|
−2 |
−1 |
1 |
2 |
3 |
4 |
x |
|
Ì
Periodische Funktion
Falls p eine Periode der Funktion f ist, dann ist auch k p für alle ganzen Zahlen k Z eine Periode von f. Charakterisierend für periodische Funktionen ist die kleinste positive Periode. Bei periodischen Funktionen wiederholt sich eine Art Funktionsprototyp im Abstand der kleinsten positiven Periode.
Periodische Funktionen treten insbesondere bei zeitabhängigen Prozessen auf. Bei zeitabhängigen Funktionen bezeichnet man die kleinste positive Periode als Schwingungsdauer und den Kehrwert als Frequenz.
Definition 5.22 (Schwingungsdauer und Frequenz)
Bei einer zeitabhängigen Funktion mit Periode p bezeichnet man die Periode auch als
Schwingungsdauer T und nennt f = T1 die Frequenz.

5.3 Eigenschaften |
189 |
Je größer also die Schwingungsdauer ist, um so kleiner ist die Frequenz. Umgekehrt besitzt eine periodische Funktion mit großer Frequenz eine kleine Schwingungsdauer. Zeit und Frequenz sind physikalische Größen, die mit Einheiten versehen sind. Die Zeit wird üblicherweise in Sekunden mit dem Einheitenzeichen s angegeben. Für die Frequenz ver-
wendet man die Einheit Hertz: 1 Hz = 1 . s
5.3.3 Monotonie
Funktionen, deren Funktionswerte mit zunehmenden x-Werten ständig anwachsen, nennt man monoton wachsend. Umgekehrt bezeichnet man Funktionen, deren Funktionswerte mit zunehmenden x-Werten ständig abnehmen, als monoton fallend. Bei der strengen Monotonie müssen die Funktionswerte tatsächlich anwachsen oder abnehmen, sie dürfen nicht konstant bleiben.
Definition 5.23 (Monotonie)
Eine Funktion f ist auf dem Intervall I
L |
monoton fallend, falls |
f x1 |
f x2 |
, |
||
streng monoton fallend, falls |
f |
(x1) ≥ f |
(x2), |
|||
L |
monoton wachsend, falls |
f |
(x1) > f |
(x2), |
||
L |
streng monoton wachsend, falls |
f |
(x1) ≤ f |
(x2), |
||
L |
|
|
( |
) < |
( |
) |
für alle Zahlen x1 und x2 aus dem Intervall I mit der Eigenschaft x1 < x2.
Der entscheidende Punkt in dieser Definition ist, dass man alle möglichen Kombinationen von x1-Werten und x2-Werten betrachten muss. Für praktische Zwecke ist die Beurteilung der Monotonie mithilfe dieser Definition meist wenig hilfreich. Alternative Vorgehensweisen zur Bestimmung der Monotonieeigenschaften werden wir im Abschnitt 6.4.2 mithilfe der Di erenzialrechnung kennenlernen.
Wenn man Aussagen über die Monotonie einer Funktion macht, dann muss man stets angeben, auf welchem Intervall man die Funktion betrachtet. Ohne Angabe eines Intervalls beziehen sich Monotonieaussagen auf den komplette Definitionsbereich der Funktion.
Konstante Funktionen nehmen bezüglich der Monotonie eine Sonderrolle ein. Sie sind sowohl monoton fallend als auch monoton wachsend.
190 |
5 Funktionen |
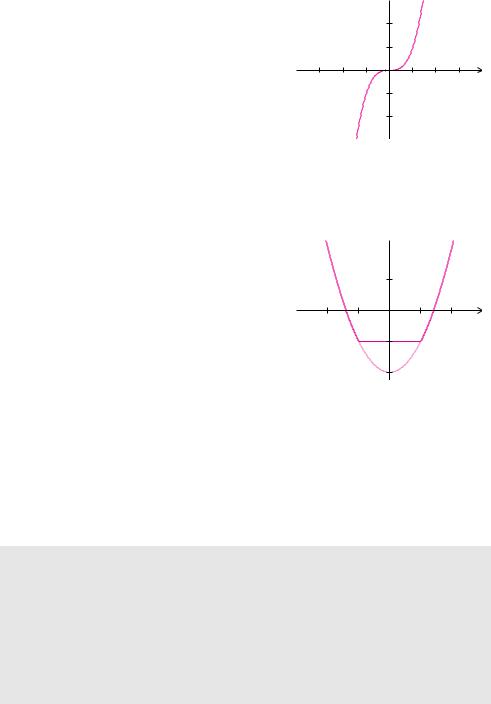
Beispiel 5.42 (Streng monoton wachsende Funktion)
Die Funktion
f(x) = x3
ist auf der ganzen Menge der reellen Zahlen streng monoton wachsend. Skeptiker argumentieren an dieser Stelle oft damit, dass die Funktion aufgrund des horizontalen Verlaufs an der Stelle x = 0 nur monoton und nicht streng monoton wachsend ist. Diese Behauptung ist jedoch falsch, denn wäre die Funktion nicht streng monoton wachsend, dann müssten wir zwei verschiedene Werte x1 < x2 angeben können, sodass die Bedingung x31 ≥ x32 erfüllt ist. Aber solche Werte gibt es nicht.
Beispiel 5.43 (Monotonie)
Die abschnittsweise definierte Funktion
¢
¨ −1 für x [−1, 1]
¨
f(x) = ¦
¨ x2 − 2 sonst
¨
¤
ist auf dem Intervall (−∞, −1] streng monoton und auf dem Intervall (−∞, 1] monoton fallend. Auf dem Intervall [1, ∞) ist sie streng monoton und auf dem Intervall [−1, ∞) monoton wachsend. Die Funktion ist auf dem Intervall [1, −1] konstant, also sowohl monoton fallend als auch monoton wachsend.
y 
2f (x) = x3
1
−3 −2 −1 |
1 2 3 |
x |
|
−1
−2
Ì
y 
f (x)
−1
−2 −1 |
1 |
2 |
x |
|
−1
x2 − 2
−2
Ì
5.3.4 Beschränktheit
Für beschränkte Funktionen kann man eine feste obere Schranke angegeben, die kein Funktionswert jemals übersteigt und eine feste untere Schranke, die kein Funktionswert jemals unterschreitet.
Definition 5.24 (Beschränktheit)
Eine Funktion f ist auf dem Intervall I
Lnach unten beschränkt, falls die Funktionswerte aller Zahlen x aus dem Intervall I oberhalb einer unteren Schranke liegen,
Lnach oben beschränkt, falls die Funktionswerte aller Zahlen x aus dem Intervall I unterhalb einer oberen Schranke liegen.
Eine Funktion, die nach unten und nach oben beschränkt ist, heißt beschränkt.
