
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

622 |
16 Laplace-Transformation |
Wir kennen für die Lösungen x und y im Zeitbereich noch keine expliziten Formeln. Trotzdem ermöglichen die Grenzwertsätze aus Satz 16.10 bereits Aussagen über das Langzeitverhalten der Lösungen
t→∞ ( |
) = s→0 ‰ |
s X |
( |
)Ž = ∞ |
, |
t→∞ |
( |
) = s→0 |
‰ |
( )Ž = ∞ |
. |
lim x t |
lim |
s |
|
lim y |
t |
lim |
s Y |
s |
Mit den Nennernullstellen s1 = 0, s2 = −1 und s3 = 12 lässt sich die Rücktransformation durch eine Partialbruchzerlegung bestimmen:
X |
|
|
3 |
|
4 |
|
1 |
|
Y |
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
−s |
+ |
s 21 |
− |
s 1 |
= |
−s |
+ |
s 21 |
|
|||||||
|
|
|
|||||||||||||||
|
|
|
|
− |
|
+ |
|
|
= |
−2 |
+ |
|
− |
|
|||
x = |
−3 + |
4 e 21 t − |
e−t |
y |
2 e 21 t |
Ì |
|||||||||||
Lineare Di erenzialgleichungssysteme mit konstanten Koe zienten
Die Laplace-Transformation kann man zur Lösung linearer Di erenzialgleichungssysteme mit konstanten Koe zienten verwenden. Dabei ist im Bildbereich ein lineares Gleichungssystem mit Parameter zu lösen.
Das Di erenzialgleichungssystem aus Beispiel 16.17 lässt sich auch durch Einführen von Zustandsgrößen mit den Methoden aus Abschnitt 12.5 lösen. Dabei entstehen jedoch (4, 4)-Matrizen. Im Gegensatz dazu erzeugt die Laplace-Transformation lediglich ein Gleichungssystem, das sich mit einer (2, 2)-Matrix beschreiben lässt.
16.7 Anwendungen
Eine der wichtigsten Anwendungen der Laplace-Transformation ist die Regelungstechnik. Die klassische Regelungstechnik kombiniert die Theorie linearer zeitinvarianter Systeme mit der Laplace-Transformation. Wir beziehen uns in diesem Abschnitt auf die Begri e und Ergebnisse aus Abschnitt 15.6.1.
16.7.1 Regelungstechnik
Die Regelungstechnik ist ein Teil der Automatisierungstechnik, die sich mit dem Messen, Steuern und Regeln technischer Systeme beschäftigt. Im Gegensatz zur reinen Steuerung erfolgt beim Regeln ein Abgleich zwischen Sollund Istwerten. Durch negative Rückkopplung entsteht dabei ein geschlossener Regelkreis. Wir betrachten ausschließlich lineare Übertragungsglieder, die sich mathematisch als lineare zeitinvariante Systeme beschreiben lassen, siehe Abschnitt 15.6.1. Solche Übertragungsglieder lassen sich im Zeitbereich durch lineare Di erenzialgleichungen in der Form
an x(on) + . . . + a2 x¨o + a1 x˙o + a0 xo = bm x(im) + . . . + b2 x¨i + b1 x˙i + b0 xi

16.7 Anwendungen |
623 |
darstellen. Es besteht also ein linearer Zusammenhang zwischen dem Eingangssignal xi inklusive seiner Ableitungen bis zur Ordnung m und dem Ausgangssignal xo inklusive seiner Ableitungen bis zur Ordnung n. Typischerweise sind zum Zeitpunkt t = 0 alle Funktionswerte und Werte der Ableitungen sowohl des Eingangsals auch des Ausgangssignals null. Wir transformieren die Di erenzialgleichung deshalb mit Nullanfangsbedingungen
|
|
( |
0 |
) = |
0, x˙ |
|
( |
0 |
) = |
(i |
|
) |
( |
0 |
) = |
0, x |
|
( |
0 |
) = |
0, x˙ |
|
( |
0 |
) = |
( |
|
) |
( |
0 |
) = |
0 |
x |
i |
i |
0, . . . , x |
m |
|
o |
o |
0, . . . , x |
n |
|
||||||||||||||||||||||
in den |
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Bildbereich:
(an sn + . . . + a2 s2 + a1 s + a0)Xo(s) = (bm sm + . . . + b2 s2 + b1 s + b0)Xi(s).
Nach Definition 15.7 ist die Übertragungsfunktion G das Verhältnis von Ausgangssignal im Bildbereich Xo zum Eingangssignal im Bildbereich Xi:
|
|
|
Xo |
s |
|
bm sm |
. . . |
b s2 |
|
b1 s b0 |
||||
G |
s |
) = |
Xi |
(s) |
= |
an sn |
+. . . |
|
+a22s2 |
+a1 s |
+a0 |
. |
||
( |
|
|
( ) |
|
+ |
|
+ |
+ |
|
+ |
|
|||
Somit ist jedes lineare Übertragungsglied durch seine Übertragungsfunktion G charakterisiert. Wenn xo das Ausgangssignal zum Eingangssignal xiist, dann gilt aufgrund der Linearität und der Zeitinvarianz des Systems
S
xi(t) Ð→ xo(t) Ô Xo(s) = G(s) Xi(s).
Dabei sind Xi und Xo die Laplace-Transformierten des Einganssignals xi und des Ausgangssignals xo.
Bei der Reihenschaltung zweier Systeme wird das Ausgangssignal des ersten Systems als Eingangssignal des zweiten Systems verwendet:
S1 |
S2 |
o2(t). |
i1(t) Ð→ |
o1(t) = i2(t) Ð→ |
Entsprechend gilt im Bildbereich
O1(s) = G1(s) I1(s) Ô O2(s) = G2(s) O1(s) = G2(s) G1(s) I1(s).
Dabei sind I1, I2 und O1, O2 die Laplace-Transformierten der Einganssignale i1, i2 und der Ausgangssignale o1, o2. Mit G1 und G2 werden die Übertragungsfunktionen der beiden Systeme S1 und S2 bezeichnet. Das Gesamtsystem mit der Eingabegröße i1 und der Ausgabegröße o2 wird im Bildbereich durch das Produkt der beiden Übertragungsfunktionen beschrieben.
Übertragungsfunktion von Systemen in Reihenschaltung
Die Reihenschaltung der beiden Systeme mit den Übertragungsfunktionen G1 und G2 ergibt ein System mit der Übertragungsfunktion
G(s) = G1(s) G2(s). |
I(s) |
G1(s) |
|
|
G2(s) |
O(s) |
||
|
|
|
|
|
|
|||
Bei der Reihenschaltung werden die Übertragungsfunktionen multipliziert.
624 |
16 Laplace-Transformation |
Dieses Ergebnis klingt auf Anhieb nicht so spektakulär wie es in Wirklichkeit ist. Es ist natürlich wesentlich eleganter, die Übertragungsfunktionen im Bildbereich zu multiplizieren anstatt im Zeitbereich Di erenzialgleichungen ineinander einzusetzen.
Bei der Parallelschaltung zweier Systeme wird ein Signal i1 als Eingangssignal von zwei Systemen verwendet. Die beiden Ausgangssignale o1 und o2 überlagern sich zu einem gemeinsamen Ausgangssignal o1 + o2. Entsprechend gilt im Bildbereich
O1(s) + O2(s) = ‰G1(s) + G2(s)ŽI1(s).
Übertragungsfunktion von Systemen in Parallelschaltung
Die Parallelschaltung der beiden Systeme mit den Übertragungsfunktionen G1 und G2 ergibt ein System mit der Übertragungsfunktion
G(s) = G1(s) + G2(s).
Bei der Parallelschaltung werden die Übertragungsfunktionen addiert.
I(s) |
|
G1(s) |
|
O(s) |
||
|
|
|||||
|
|
|
||||
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G2(s) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ein wichtiges Prinzip bei der Regelung von Systemen ist die negative Rückkopplung. Ein Eingangssignal i durchläuft dabei ein System mit Übertragungsfunktion GR des Reglers sowie Übertragungsfunktion GS der Regelstrecke und wird dann mit umgekehrtem Vorzeichen wieder dem Eingangssignal überlagert. Für die Übertragungsfunktionen bedeutet das
O(s) = GR(s) GS(s) (I(s) − O(s))
oder anders formuliert
O(s) (1 + GR(s) GS(s)) = GR(s) GS(s) I(s).
In der Praxis bedeutet dies, dass die Regelgröße o mit der Führungsgröße i verglichen wird. Der Regler beeinflusst die Regelstrecke dann so, dass die Regelabweichung i − o möglichst klein wird.
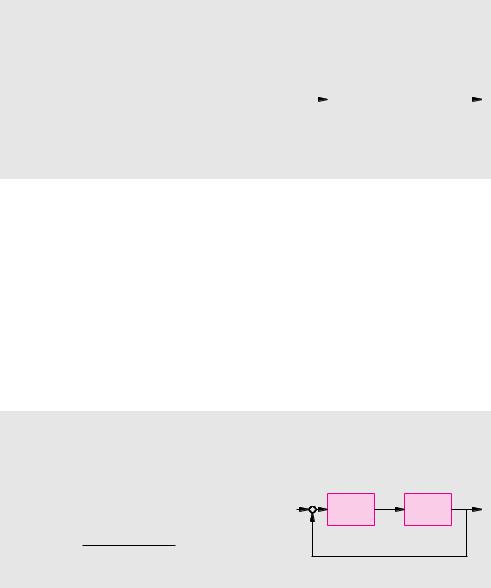
Übertragungsfunktion von Systemen mit negativer Rückführung
Bildet man aus der Reihenschaltung der beiden Systeme mit den Übertragungsfunktionen GR und GS ein System mit negativer Rückführung, dann entsteht ein System mit der Übertragungsfunktion
G(s) = GR(s) GS(s) . 1 + GR(s) GS(s)
I(s) |
GR(s) |
GS(s) O(s) |
− |
|
|
