
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

5.5 Grenzwert und Stetigkeit |
211 |
Satz 5.20 (Zwischenwertsatz)
Kennt man zwei Funktionswerte f(a) und f(b) einer stetigen Funktion f, dann nimmt f auf dem Intervall [a, b] auch jeden Wert zwischen f(a) und f(b) mindestens einmal an.
y 
f (x)
f (b)
f (a)
a |
b x |
Eine direkte Folgerung aus dem Zwischenwertsatz ist der Nullstellensatz. Er garantiert die Existenz einer Nullstelle, falls eine stetige Funktion an einer Stelle negativ und an einer anderen positiv ist. Diese Garantie über das Vorhandensein einer Nullstelle wird beim Bisektionsverfahren in Abschnitt 5.8.2 ausgenutzt.
Satz 5.21 (Nullstellensatz)
Hat eine stetige Funktion f zwei Funktionswerte f(a) und f(b) mit unterschiedlichem Vorzeichen, dann hat die Funktion zwischen a und b mindestens eine Nullstelle.
5.5.4 Asymptotisches Verhalten
Welches Verhalten haben Funktionen, wenn man für x Werte einsetzt, die gegen ∞ oder −∞ gehen? Dieser Frage werden wir in diesem Abschnitt nachgehen. Das Verhalten einer Funktion für x-Werte gegen ∞ oder −∞ bezeichnet man als asymptotisches Verhalten. Bei zeitabhängigen Funktionen beschreibt die Asymptotik das Langzeitverhalten. Aussagen über das Langzeitverhalten von naturwissenschaftlichen und technischen Prozessen sind im Experiment oft schwer zu ermitteln. Deshalb versucht man, das Langzeitverhalten mithilfe mathematischer Modelle zu bestimmen.
Bei Folgen haben wir das Prinzip der asymptotischen oberen Schranke bereits kennengelernt. Ein ähnliches Prinzip beschreibt auch das asymptotische Verhalten von Polynomen. Grob formuliert verhält sich ein Polynom asymptotisch genau gleich wie das Glied mit der höchsten Potenz.
Asymptotisches Verhalten von Polynomen
Ein Polynom f vom Grad n
f(x) = a0 + a1 x + a2 x2 + a3 x3 + . . . + an xn, an ≠ 0
verhält sich asymptotisch gleich wie das Glied mit der höchsten Potenz. Wir verwenden die Schreibweise
a0 + a1 x + a2 x2 + a3 x3 + . . . + an xn ≈ an xn für x → ±∞.
212 |
5 Funktionen |
Asymptotische Gleichheit bedeutet, dass das Verhältnis des Polynoms zum Glied mit der höchsten Potenz im Grenzwert gegen eins geht. Die Berechnung des Grenzwerts
|
|
f x |
|
|
|
|
a0 |
|
a1 x |
|
a2 x2 |
|
a3 x3 |
|
. . . |
|
an xn |
||
|
→±∞ |
|
n( ) |
= |
|
→±∞ |
|
+ |
|
+ |
|
+ |
|
|
+ |
|
+ |
|
|
x |
lim |
a |
x |
n |
x |
lim |
|
|
|
|
an x |
n |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lässt sich durch Division durch das Glied mit der höchsten Potenz direkt durchführen:
|
f x |
|
|
a0 |
|
|
|
a1 |
|
a2 |
|
a3 |
|
|
|
|
|
|
|||||||
x→±∞ |
an(x) |
= x→±∞ |
|
|
|
+ |
|
|
+ |
|
|
+ |
|
|
+ |
|
+ |
|
= |
|
|||||
an x |
|
|
an x −1 |
an x −2 |
an x −3 |
|
|
|
|||||||||||||||||
lim |
n |
lim |
|
|
|
n |
|
|
n |
|
|
n |
|
|
n |
|
. . . |
|
1 |
|
1. |
||||
|
|
|
´¹¹¹¹¹¸¹¹¹¹¶ |
´¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¶ |
´¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¶ |
´¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
→ |
0 |
|
|
→ |
0 |
|
|
→ |
0 |
|
|
→ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
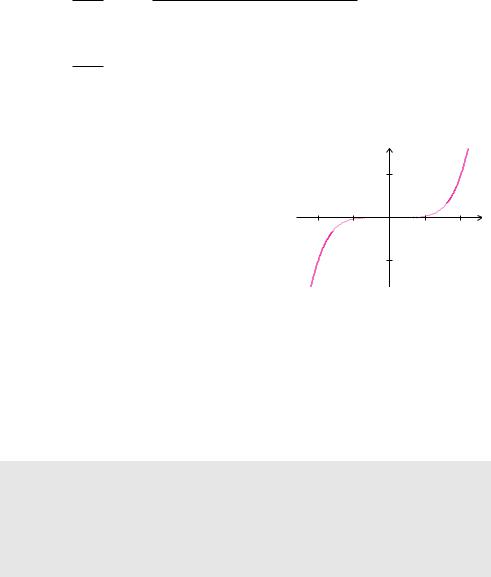
Beispiel 5.59 (Asymptotisches Verhalten eines Polynoms)
Das Polynom
f(x) = x5 + 2 x4 + 7 x3 + 5 x2 + 6 x + 3
verhält sich asymptotisch gleich wie x5. Für x gegen ±∞ ähnelt das Schaubild des Polynoms dem Schaubild von x5. Für x gegen ∞ gehen die Funktionswerte des Polynoms gegen ∞ und für x gegen −∞ gehen auch die Funktionswerte gegen −∞. Das Polynom hat mindestens eine Nullstelle. Um die Existenz weiterer Nullstellen zu klären, ist eine aufwendige Untersuchung des Polynoms erforderlich, auf die wir an dieser Stelle verzichten.
|
y |
|
|
|
|
1010 |
f (x) |
|
|
−100 |
−50 |
50 |
100 |
x |
|
−1010 |
|
|
|
Ì
Das asymptotische Verhalten von Polynomen lässt sich gewinnbringend einsetzen. Bei geradem Grad haben die Grenzwerte für x gegen ∞ und −∞ dasselbe Vorzeichen, bei ungeradem Grad haben die Grenzwerte für x gegen ∞ und −∞ unterschiedliche Vorzeichen. Ein Polynom von geradem Grad ist somit entweder nach oben oder nach unten beschränkt und ein Polynom von ungeradem Grad ist weder nach oben noch nach unten beschränkt und muss aufgrund des Satzes 5.21 mindestens eine Nullstelle besitzen.
Asymptotisches Verhalten von Polynomen
Polynome haben das folgende asymptotische Verhalten: Ein Polynom mit
Lgeradem Grad ist entweder nach unten oder nach oben beschränkt,
Lungeradem Grad ist weder nach unten noch nach oben beschränkt und besitzt mindestens eine Nullstelle.
Das asymptotische Verhalten von Polynomen lässt sich ohne großen Aufwand bestimmen. Deshalb versucht man für beliebige Funktionen Näherungsfunktionen in Form von Polynomen zu bestimmen. Eine Näherungsfunktion einer Funktion bezeichnet man als Asymptote, wenn sie sich im Grenzwert für x gegen ∞ oder −∞ nicht von der Funktion unterscheidet.

5.5 Grenzwert und Stetigkeit |
213 |
Beispiel 5.60 (Waagrechte Asymptote)
Die gebrochenrationale Funktion
f(x) = x − 2 = 1 − 2
xx
nähert sich für x gegen ±∞ dem Funktionswert y = 1. Die Näherungskurve y = 1 bezeichnen wir als waagrechte Asymptote. Im Grenzwert für x gegen ±∞ stimmt die Funktion mit der Asymptote überein, denn der Unterschied zwischen Funktion und Asymptote geht im Grenzwert gegen null,
lim |
|
f |
x |
1 |
lim |
|
2 |
|
|
0. |
|
( |
−x |
= |
|||||||||
x→±∞ |
|
( ) − |
|
) = x→±∞ |
|
||||||
|
|
y |
|
|
|
|
8 |
|
|
f (x) = x−x2 |
5 |
|
|
|
|
y = 1 |
|
||
|
|
|
|
|
−10 |
−5 |
5 |
10 |
x |
|
||||
|
|
−5 |
|
|
|
|
−8 |
|
|
Ì
In Beispiel 5.60 nähert sich die Funktion für x → ±∞ einem festen Wert. In solchen Fällen spricht man von einer waagrechten Asymptote.
Definition 5.44 (Waagrechte Asymptote)
Besitzt eine Funktion für x gegen ∞ den Grenzwert g, also
lim f(x) = g,
x→∞
dann ist die horizontale Gerade y = g eine waagrechte Asymptote für x → ∞. Entsprechendes gilt für x → −∞.
Bei Funktionen, die sich für x → ±∞ nicht einem festen Wert annähern, wird das asymptotische Verhalten durch kompliziertere Näherungsfunktionen beschrieben. In der Regel versucht man Näherungsfunktionen in Form von Polynomen, insbesondere in Form von Geraden, zu bestimmen. Im Prinzip sind jedoch auch andere Funktionen als Näherungsfunktionen möglich.
Definition 5.45 (Schiefe Asymptote)
Unterscheidet sich eine Funktion für x gegen ∞ von einer Näherungskurve g(x) nicht, also
lim (f(x) − g(x)) = 0,
x→∞
dann ist die Funktion g(x) eine schiefe Asymptote für x → ∞. Entsprechendes gilt für x → −∞.
214 |
5 Funktionen |
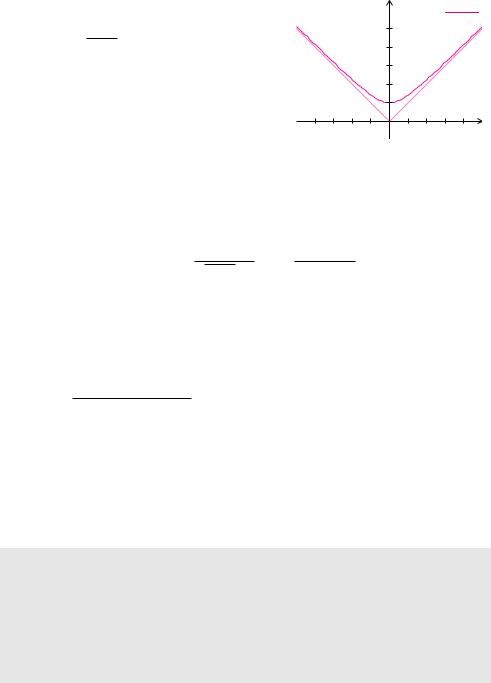
Beispiel 5.61 (Schiefe Asymptote)
Wir vermuten, dass das asymptotische Verhalten der Funktion
√
f(x) = x2 + 1
für x → ∞ durch die Gerade y = x beschrieben wird. Zum Nachweis unserer Vermutung betrachten wir den Grenzwert
xlim |
f |
x |
|
x |
|
xlim |
√ |
|
|
|
x . |
) − |
) = |
x2 |
+ |
1 |
|||||||
→∞ |
( ( |
|
|
→∞ |
Š |
|
− • |
||||
y |
f (x) = px2 + 1 |
5 |
|
4 |
|
3 |
|
2 |
|
1 |
y = |x| |
−4 −3 −2 −1 |
1 2 3 4 x |
Die Berechnung des Grenzwertes erfordert ein trickreiches Vorgehen. Dazu erweitern wir den Term geeignet.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
||||||||
limx |
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x2 |
|
1 |
|
|
x |
|
x2 |
|
1 |
|
x |
|
|
||||||||||
|
f x x |
|
|
|
x2 |
|
1 |
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Š |
|
|
|
+ |
|
|
−x2 |
• Š1 x |
+ |
|
+ |
|
• |
||||||||||||||||||||
|
|
( ( ) − ) = |
x |
→∞ |
|
√ |
|
|
|
|
|
|
|
|
x |
→∞ |
1 |
|
|
|
|
|
|||||||||||||||||||
|
→∞ |
|
Šx |
|
|
|
|
1+ − • = |
|
|
|
|
|
√ |
0+. |
+ |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
xlim |
|
|
2 |
|
|
|
|
|
x2 |
|
xlim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x2 |
|
|
1 |
|
|
x |
|
|
x2 |
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|||||||||||||
|
|
= |
|
→∞ |
|
√ |
|
+ − |
|
|
|
= |
→∞ |
√ |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Aus Symmetriegründen muss |
y |
|
x |
eine |
Asymptote für x |
|
|
|
sein. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
= − |
|
+ |
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ −∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Echt und unecht gebrochenrationale Funktionen besitzen unterschiedliches asymptotisches Verhalten. Bei einer echt gebrochenrationalen Funktion ist der Grad im Zähler n kleiner als der Grad im Nenner m. Deshalb gilt
|
b0 |
|
b1x . . . bmx |
|
|
|
|
a0 |
0+ |
|
|
a1 |
+ |
|
+ |
|
an |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
− |
|
|
||||||||||||
|
a0 |
+ |
a1x |
+ |
. . . |
+ |
anxn |
|
|
|
|
m |
|
|
|
|
m 1 |
|
|
. . . |
|
|
m n |
|
|||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
. . . bm |
|
|
|||||||
lim |
|
+ |
+ + |
|
|
= |
|
lim |
|
xm |
+ xm−1 + + |
= |
0. |
||||||||||||||
→±∞ |
|
|
|
x |
→±∞ |
|
|
||||||||||||||||||||
x |
|
|
|
|
|
|
|
m |
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
Somit ist die x-Achse eine waagrechte Asymptote. Bei unecht gebrochenrationalen Funktionen entscheidet der Unterschied zwischen dem Grad im Zähler n und dem Grad im Nenner m über das asymptotische Verhalten. In Beispiel 5.60 stimmen Zählerund Nennergrad überein, die Funktion hat dann eine waagrechte Asymptote. Bei einer unecht gebrochenrationalen Funktion ergibt sich durch Polynomdivision ein Polynom vom Grad n − m und ein Rest, der für x → ±∞ gegen null geht.
Asymptotisches Verhalten gebrochenrationaler Funktionen
Gebrochenrationale Funktionen haben das folgende asymptotische Verhalten:
LEcht gebrochenrationale Funktionen haben für x → ±∞ die x-Achse als waagrechte Asymptote.
LBei unecht gebrochenrationalen Funktionen findet man waagrechte und schiefe Asymptoten durch Polynomdivision.
