
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
6.7 Aufgaben |
289 |
6.7 Aufgaben
Verständnisaufgaben
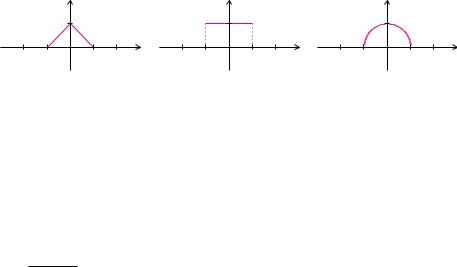
Aufgabe 6.1
Wo sind die skizzierten Funktionen di erenzierbar? Skizzieren Sie die Ableitungsfunktionen.
a) |
|
y |
|
b) |
|
|
|
|
|
|
|
1 |
|
|
−2 |
−1 |
1 |
2 |
x |
|
|
|
y |
|
c) |
|
|
|
|
|
|
|
1 |
|
|
−2 |
−1 |
1 |
2 |
x |
|
|
|
y |
|
|
|
|
1 |
|
|
−2 |
−1 |
1 |
2 |
x |
|
Aufgabe 6.2
Gibt es Funktionen, die für alle reellen Zahlen definiert und überall stetig, aber an unendlich vielen Stellen nicht di erenzierbar sind?
Aufgabe 6.3 |
) = |
|
|
|
( |
|
) = |
3 |
|
|
Die Schaubilder der beiden Funktionen f x |
|
x3 |
und g |
x |
x2 |
besitzen zwei gemeinsame |
||||
( |
|
|
|
|
|
|
|
|||
Punkte. Bestimmen Sie die Steigungen der |
Tangenten in diesen beiden Punkten und skizzieren |
|||||||||
|
√ |
|
|
|
|
√ |
|
|
||
Sie damit die beiden Schaubilder in einem gemeinsamen Koordinatensystem.
Aufgabe 6.4
Die folgenden Grenzwerte haben alle die Form eines Di erenzialquotienten. Bestimmen Sie die Grenzwerte mithilfe der Ableitung.
a) lim |
e−2Δx |
1 |
b) lim |
|
|
2 |
|
x |
3 |
8 |
|
sin |
|
π |
x |
|
1 |
|
|
|
|
|
c) lim |
|
6 |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x→0 |
x− |
|
x→0 |
( |
|
+ |
x) − |
|
|
x→0 |
|
( |
|
+ x |
) − |
|
||
Aufgabe 6.5
Wahr oder falsch? Ein Polynom vom Grad n ist genau n-mal di erenzierbar.
Aufgabe 6.6
Bei den folgenden Polynomen sind a0, a1, a2, . . ., an−1, an beliebige reelle Konstanten. Bestimmen Sie alle Ableitungen der Polynome.
a) f(x) = anxn + an−1xn−1 + . . . + a1x + a0 b) f(x) = (a1x + a0)n
Aufgabe 6.7
Für einen beliebigen reellen Parameter a betrachten wir die Funktion
f(x) = (a − x) (a + x) .
a)Berechnen Sie die Ableitung von f direkt mit der Produktregel.
b)Vereinfachen Sie die Funktion f zuerst mithilfe der dritten binomischen Formel und berechnen Sie dann die Ableitung.
Aufgabe 6.8
Unter welchem Winkel schneiden sich die Schaubilder der Funktionen f1(x) = sin x und f2(x) = cos x im Bereich x [0, π]?

290 6 Di erenzialrechnung
Rechenaufgaben
Aufgabe 6.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Bestimmen Sie für die folgenden Funktionen die erste Ableitung. |
|
|
x2 |
− |
1 |
||||||||||||||||||||
a) f |
|
x |
|
|
1 |
|
x2 |
10 |
b) f |
|
x |
|
|
x |
|
|
|
||||||||
|
|
( |
|
) = ‰ |
|
− |
|
Ž |
|
( |
|
) = |
|
|
|
|
c) f x |
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
f x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
f x |
tan |
|
3 x |
|||||
d) |
|
cosh |
|
e) f x |
|
ln+ x |
f) |
|
|||||||||||||||||
|
|
( |
) = |
|
|
|
|
|
|
( ) = |
|
√ |
|
( ) = |
|
|
|
( |
) |
||||||
Aufgabe 6.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Bei den folgenden Funktionen sind C, δ, ω und ϕ beliebige reelle Konstanten. Bestimmen Sie für jede Funktion die erste und die zweite Ableitung.
a) f |
t |
4 e |
− |
t |
2t 3 |
b) f |
t |
3 sin |
2t |
) |
|
|
c) f |
t |
3 t2 e |
− |
2t |
|
ωt |
|||
d) f |
t |
|
t cos |
e) f |
(t) = C cos( |
|
|
|
f) f |
t |
C e |
− |
|
|
sin |
|
||||||
|
( ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) = |
|
|
|
|
|
|
|
|
( ) = − |
|
|
|
( − ) |
|
( ) = |
|
ωt |
ϕ |
) |
|
|
|
δt |
|
|
|
||||
|
|
|
|
|
( − |
|
|
( ) = |
|
|
|
|
|
( |
) |
|||||||
Aufgabe 6.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Bei den folgenden Funktionen ist a eine beliebige reelle Konstante. Bestimmen Sie jeweils die erste Ableitung.
a) f x |
1 |
|
|
|
|
b) f x |
|
|
|
|
|
x |
|
|
|
|
|
|
c) f x |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
a |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
d) f(x) = |
|
|
|
|
|
|
|
e) f (x) = ln x a |
|
|
|
|
(x) = |
1 |
|
|
|
|
|
|
x |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
x |
|
|
a |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
f) f |
|
|
|
|
arctan |
|
|
|
|
|||||||||||||||
|
|
( ) = √+ |
+ |
|
|
( ) = ( + ) |
|
|
|
( ) = |
a |
|
|
+ |
|
|
|
a |
|
|
||||||||||||||||||||||||
Aufgabe 6.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Bestimmen Sie für die folgenden Funktionen jeweils die erste Ableitung. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
a) r |
( |
ϕ |
) = |
»1 |
+ |
|
cos ϕ |
b) A ω |
|
cos |
‹ |
|
1 |
|
|
c) p |
( |
h |
) = |
p0 e− |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
p0 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
1 |
− |
ω |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
( ) = |
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Aufgabe 6.13 |
|
|
|
|
|
( |
|
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
An welcher Stelle hat die Funktion f |
x |
2x |
eine Tangente mit Steigung 1? |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Aufgabe 6.14 |
|
|
|
|
|
|
|
|
|
|
|
ersten drei Ableitungen f |
, f |
′′ |
und f |
′′′ |
und leiten |
|||||||||||||||||||||||||||
Bestimmen Sie für die folgenden Funktionen die |
n |
ab. |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Sie daraus eine Formel für die n-te Ableitung f |
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
a) |
f x |
xn |
|
|
|
|
b) f x |
|
|
e− |
2 x |
|
|
c) |
f x |
sin 3x |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) = |
2 |
x |
( ) |
|
|
|
|
||||||||||||||||
d) f(x) = ln x |
|
|
|
|
e) f x |
) = |
|
|
1 |
|
|
|
|
|
|
f) f |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
( ) = |
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
( ) = |
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Aufgabe 6.15 |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Untersuchen Sie, ob folgende Funktionen di erenzierbar sind: Skizzieren Sie die Schaubilder der Funktionen und der ersten Ableitungen.
|
|
|
|
|
|
|
|
|
|
1 |
x 1 |
2 |
|
für |
x |
≤ |
0 |
a) f |
x |
x |
+ |
1 |
S |
b) f |
( |
x |
) = œ |
cosS −x S |
|
für |
x |
0 |
|||
|
( ) = S |
|
|
|
|
|
+ ( + |
|
) |
|
|
> |
|
Aufgabe 6.16
An welchen Stellen hat das Schaubild der Funktion f(x) = cos ‹ x• ex waagrechte Tangenten?
2

6.7 Aufgaben |
291 |
Aufgabe 6.17
Leiten Sie mithilfe der Regel für die Ableitung der Umkehrfunktion die Formel für die Ableitung des Arkuskosinus
(arccos x)′ = √ −1
1 − x2
her. Gehen Sie dabei wie bei der Herleitung der Ableitungsformel für den Arkussinus vor. Warum ist die Ableitung des Arkuskosinus immer negativ?
Aufgabe 6.18
Wie oft sind die folgenden abschnittsweise definierten Funktionen di erenzierbar? Skizzieren Sie die Schaubilder von f, f′ und f′′.
a) f x |
3 1 |
x2 |
für |
x |
|
1 |
b) f x |
¢ |
4 |
√ |
5 |
|
|
|
für |
|
|
|
|
|
||
|
1 |
− |
x3 |
für |
x |
< |
1 |
|
¨ |
5 |
|
|
|
|
|
|
|
4 |
|
|
0 |
|
|
|
|
|
|
16 |
|
x2 |
|
|
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
¨ |
5 |
|
|
|
x |
|
|
x |
|
0 |
|
|
|
( ) = œ |
|
( |
− ) |
|
|
≥ |
|
|
¨ |
|
|
|
|
|
− |
|
für |
− |
|
≤ |
|
≤ |
|
|
|
|
|
|
|
32 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
( |
) = ¦ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
− |
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Aufgabe 6.19
Bestimmen Sie die Konstanten a0, a1 und a2 jeweils so, dass bei den abschnittsweise definierten
Funktionen die Funktion selbst sowie die Ableitungen f′ und f′′ stetig sind. Skizzieren Sie jeweils f, f′ und f′′.
a) f |
x |
|
ex |
|
a1 x |
|
a2 x2 |
|
|
für |
x |
1 |
b) f |
|
|
x |
|
|
ln x |
a1 x |
|
a2 x2 |
für |
x |
≤ |
2 |
|
||||
|
a0 |
+ |
+ |
|
|
für |
x ≤ |
1 |
( |
) = œ |
a0 |
+ |
+ |
für |
x |
2 |
|
||||||||||||||
|
( ) = œ |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
> |
|
|
||||||||||
Aufgabe 6.20 |
|
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Die implizite Gleichung |
1 beschreibt eine Ellipse mit Mittelpunkt im Koordinatenur- |
||||||||||||||||||||||||||||||
2 |
|
b |
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
0 und b |
|
|
0 so, dass die beiden Punkte P 0 2 |
und |
||||||||||||||
|
|
|
|
|
|
|
|
Halbachsen a |
|
|
|
||||||||||||||||||||
sprung. Bestimmen Sie die + |
|
|
= |
|
Punkt R 2 Ry |
|
liegt auf der Ellipse. Welche y-Koordinate |
||||||||||||||||||||||||
Q 3 0 |
auf der Ellipse liegen. Auch der |
|
|||||||||||||||||||||||||||||
( S ) |
|
> |
( S |
|
> |
) |
|
|
|
|
|
|
|
|
( |
S |
) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
hat der Punkt R? Bestimmen Sie die Tangente an die Ellipse im Punkt R und skizzieren Sie die Ellipse samt Tangente im Punkt R.
Aufgabe 6.21
Bestimmen Sie die folgenden Grenzwerte:
|
lim |
ln |
|
2 x |
|
1 |
|
|
b) lim |
tan x |
|
|
|
|
|
|
|
||||||
a) |
x→0 |
( |
x |
+ |
|
) |
x→0 x |
||||
Aufgabe 6.22
3 − 2 e−t
Wir betrachten die Wachstumsfunktion f(t) = 4 3 + 2 e−t .
c) lim arctan x
x→0 x
a)Welchen maximalen Definitionsbereich hat die Funktion f? Wo ist die Funktion stetig und wo ist sie di erenzierbar?
b)Bestimmen Sie alle waagrechten Asymptoten der Funktion f.
c)Berechnen Sie alle Nullstellen, Hochpunkte, Tiefpunkte und Wendepunkte der Funktion f.
d)Ist die Funktion f beschränkt? Welche Monotonieeigenschaften hat die Funktion?
e)Skizzieren Sie das Schaubild der Funktion f und geben Sie den Wertebereich an.

292 |
6 Di erenzialrechnung |
Aufgabe 6.23 |
√ |
x − x
Wir betrachten die zusammengesetzte Funktion f(x) = œ √
− −x − x
für x |
≥ |
0 |
auf R. |
für x |
0 |
||
|
< |
|
|
a)Untersuchen Sie die Funktion f auf Symmetrie.
b)Ist f an der Stelle x = 0 stetig bzw. di erenzierbar?
c)Bestimmen Sie alle Nullstellen, Extremwerte und Wendepunkte der Funktion f.
d)Skizzieren Sie die Funktion f mit allen bekannten Eigenschaften.
Aufgabe 6.24 |
1 |
|
|
|
7 |
|
|
|
5 |
|
Wir betrachten das Polynom f(x) = |
x |
3 |
− |
x |
2 |
− 2 x + |
. |
|||
5 |
|
10 |
|
2 |
a)Welchen maximalen Definitionsbereich hat die Funktion f? Wo ist die Funktion stetig und wo ist sie di erenzierbar?
b)Zeigen Sie, dass x = 1 eine Nullstelle von f ist, und bestimmen Sie alle weiteren Nullstellen.
c)Berechnen Sie alle Hochpunkte, Tiefpunkte und Wendepunkte der Funktion f.
d)Ist die Funktion f beschränkt? Welche Monotonieeigenschaften hat die Funktion?
e)Skizzieren Sie das Schaubild der Funktion f und geben Sie den Wertebereich an.
Aufgabe 6.25
Gegeben ist die gebrochenrationale Funktion −(x − 2)2 . x + 2
a)Welchen maximalen Definitionsbereich besitzt die Funktion f?
b)Welches asymptotische Verhalten hat f für x → ±∞?
c)Bestimmen Sie alle Schnittpunkte mit der x-Achse und der y-Achse.
d)Besitzt die Funktion f Polstellen? Wenn ja, finden Vorzeichenwechsel statt?
e)Bestimmen Sie alle Extremwerte und Wendepunkte der Funktion f.
f)Skizzieren Sie die Funktion f mit allen bisher bestimmten Eigenschaften.
Aufgabe 6.26 |
|
|
|
|
A t |
|
|
|
> |
|
|
Wir betrachten die Sättigungsfunktion f t |
|
für t |
|
0 mit dem Parameter A |
0. |
||||||
t |
|
|
|||||||||
|
f |
|
|
|
A |
|
|
|
|||
a) Wo ist die Funktion |
stetig und wo |
ist sie di erenzierbar? |
|
||||||||
|
( ) = |
|
+ |
|
|
≥ |
|
|
|||
b) Berechnen Sie alle Nullstellen, Hochpunkte, Tiefpunkte und Wendepunkte der Funktion f.
c) Ermitteln Sie den Sättigungswert lim f(t).
x→∞
d)Ist die Funktion f beschränkt? Welche Monotonieeigenschaften hat die Funktion?
e)Zu welchem Zeitpunkt wird der halbe Sättigungswert erreicht?
f)Bestimmen Sie die Tangente der Funktion f an der Stelle t = 0.
g)Skizzieren Sie das Schaubild der Funktion f und geben Sie den Wertebereich an.

6.7 Aufgaben |
293 |
Aufgabe 6.27
Wir betrachten die Funktion f(x) = √ x .
16 − x2
a)Welchen maximalen Definitionsbereich und welche Symmetrieeigenschaften besitzt die Funktion f? Wie verhält sich die Funktion am Rand des maximalen Definitionsbereichs?
b)Wo ist die Funktion f stetig und wo ist sie di erenzierbar?
c)Bestimmen Sie sämtliche Nullstellen, Hochpunkte, Tiefpunkte und Wendepunkte.
d)Ist die Funktion beschränkt? Welche Monotonieeigenschaften hat die Funktion?
e)Skizzieren Sie das Schaubild der Funktion und geben Sie den Wertebereich an.
Aufgabe 6.28
Wir betrachten die Funktionenschar ft(x) = − 1 x4 + x2 + 3 t für t > 0.
2t 2
a)Untersuchen Sie die Funktionenschar ft auf Symmetrie und berechnen Sie alle Nullstellen.
b)Bestimmen Sie alle Extremwerte und Wendepunkte von ft.
c)Auf welcher Kurve liegen die Wendepunkte aller Funktionen ft?
d)Weisen Sie nach, dass zwei Funktionen ft1 und ft2 für verschiedene t1 ≠ t2 keinen gemeinsamen Punkt besitzen.
Anwendungsaufgaben
Aufgabe 6.29
Das sogenannte axiale Widerstandsmoment ist ein Maß für den Widerstand, den ein Körper einer Biegung entgegensetzt. Ein Rohr mit kreisförmigem Querschnitt und Durchmesser d hat
das axiale Widerstandsmoment W d |
|
π |
d3. Um wie viel Prozent darf der Durchmesser d |
|||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
32 |
|
|
|
|
|
||
höchstens abweichen, damit das |
Widerstandsmoment um höchstens 1 % vom geforderten Wert |
|||||||||||||
( |
) = |
|
|
|
|
|
|
|
||||||
abweicht? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aufgabe 6.30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Berechnen Sie Näherungswerte für alle Schnittpunkte des Schaubildes der Funktion f x |
tan x |
|||||||||||||
|
y |
|
2 x |
|
x |
|
|
|
|
|
π |
π |
sollen mit dem |
|
mit der Geraden |
|
für |
|
|
|
|
|
|
und 2 . Die Näherungswerte |
|||||
|
|
|
-Werte zwischen 2 |
( |
) = |
|||||||||
|
|
mit einer Genauigkeit von 8 Stellen nach dem Komma berechnet werden. |
||||||||||||
Newton-Verfahren = |
|
|
|
|
|
|
|
− |
|
|
|
|
||
Aufgabe 6.31
Taschenrechner und Computer verfügen nur über die Grundrechenarten Addition, Subtraktion, Multiplikation und Division. Alle anderen Berechnungen werden mithilfe numerischer Näherungsverfahren realisiert. Einen Näherungswert für a kann man berechnen, indem man das Newton-
Verfahren auf die Gleichung |
x2 |
|
a anwendet. Berechnen Sie einen Näherungswert für |
|
3 |
in |
|
= |
√ |
√ |
|||
Form eines Bruches, indem Sie zwei Schritte des Newton-Verfahrens durchführen. |
||||||
Aufgabe 6.32
Eine zylinderförmige Getränkedose soll so hergestellt werden, dass möglichst wenig Blech verbraucht wird. Welche Höhe und welchen Durchmesser hat eine optimale Getränkedose, die ein Fassungsvermögen von 0.5 Liter hat?
294 |
6 Di erenzialrechnung |
Aufgabe 6.33
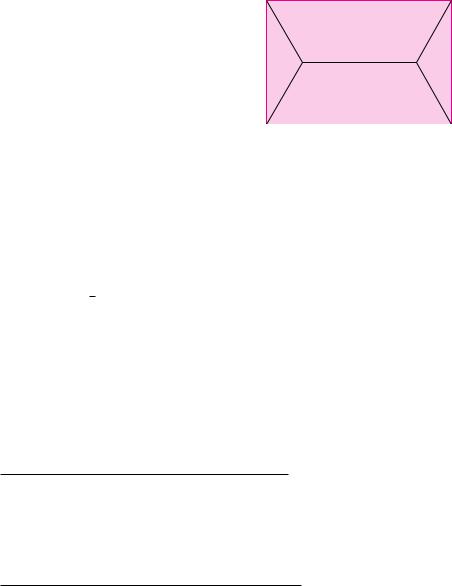
In einem Fußballstadion sollen vier Flutlichtanlagen, die sich an den Eckpunkten eines Rechtecks mit Länge ` = 120 m und breite b = 80 m befinden, durch Kabel verbunden werden. Da die Kabelführung unterirdisch erfolgt, verbindet man die Eckpunkte wie in der Abbildung eingezeichnet. Wie muss man die Längen x und y wählen, damit die Gesamtlänge L = 4 y + x minimal wird? Um wie viele Meter kürzer ist diese Verbindung im Vergleich zu einer Kabelführung entlang der Kanten des Rechtecks bzw. im Vergleich zu einer Kabelführung entlang der Diagonalen im Rechteck?
|
y |
m |
|
b = 80 |
x |
|
|
|
` = 120 m |
Aufgabe 6.34
Ein Fahrmanöver auf einer Teststrecke besteht aus drei Phasen:
1.Beschleunigen aus dem Stand von 0 ms auf 30 ms in 6 Sekunden.
2.Fahren mit konstanter Geschwindigkeit von 30 ms über eine Strecke von 150 m.
3.Bremsen aus 30 ms in den Stand mit einer Verzögerung von −10 sm2 .
Zur Beschreibung aller drei Phasen kann man folgende Bewegungsgleichung verwenden:
s(t) = s0 + v0 t + 1 a0 t2
2
a)Bestimmen Sie allgemein die ersten beiden Ableitungen s′(t) = v(t) und s′′(t) = a(t).
b)Berechnen Sie s(t), v(t) und a(t) für obige drei Phasen und skizzieren Sie die Kurven.
c)Bestimmen Sie die Gesamtzeit und den Gesamtweg des Fahrmanövers.
Aufgabe 6.35
Die Kennlinie eines Motors wird durch Messpunkte charakterisiert.
a) Gegeben sind zunächst folgende Werte:
Drehzahl |
|
|
1 |
|
|
x |
|
0 |
3000 |
5000 |
6000 |
|
|
|
min |
|
|
||||||||
Drehmoment |
|
Nm |
f |
( |
x |
) |
0 |
200 |
300 |
250 |
||
|
[ |
] |
|
|
|
|
|
|
||||
Durch die ersten beiden Messpunkte soll eine Gerade und durch den zweiten bis vierten Messpunkt soll eine Parabel gelegt werden. Es ergibt sich insgesamt eine stetige Kennlinie. Wie lauten die Funktionsgleichungen der Geraden und der Parabel?
b) Nun sind folgende Werte gegeben:
Drehzahl |
|
|
1 |
|
|
x |
0 |
3000 |
5000 |
6000 |
|
|
|
min |
|
||||||||
Drehmoment |
|
Nm |
f x |
0 |
200 |
|
|
||||
|
[ |
] |
f |
( x) |
|
1 |
0 |
− |
− |
||
|
15 |
||||||||||
|
|
|
|
|
|
′ |
|
|
|
||
Mit dem Ansatz aus Gerade und Parabel ergibt sich nun also eine stetige und di erenzierbare |
||
( ) |
− |
− |
Kennlinie. Wie lauten nun die Funktionsgleichungen der Geraden und der Parabel?
