
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

529
13 Fourier-Reihen
In diesem Kapitel beschäftigen wir uns intensiv mit periodischen Funktionen. Periodische Funktionen haben eine immense Bedeutung in den Naturwissenschaften und in der Technik. Die Analyse von Schwingungsvorgängen ist grundlegend für die Signalverarbeitung. Elektrische und mechanische Antriebe führen zu Schwingungen und damit zu periodischen Funktionen. Außerdem basieren viele Methoden in der digitalen Bildund Tonbearbeitung auf dem Verhalten periodischer Funktionen. Der Schlüssel für das Verständnis periodischer Funktionen liegt in der Darstellung mithilfe von Fourier-Reihen.
Bei der Darstellung einer Funktion durch Potenzreihen greift man eine einzige Entwicklungsstelle heraus. Potenzreihen liegt eine Annäherung von Funktionen durch Polynome zugrunde. Die Approximationsgüte dieser Polynome ist somit um so besser, je näher man sich an der gewählten Entwicklungsstelle befindet.
Für periodische Funktionen hat sich eine grundlegend andere Strategie bewährt. Die Annäherung erfolgt hier durch geeignete Kombinationen von Sinusund Kosinusfunktionen. Dabei findet die Annäherung gleichmäßig über eine volle Periode der Funktion statt. Die grundlegenden Ideen hat der französische Mathematiker Jean Baptiste Joseph Fourier Anfang des 19. Jahrhunderts verö entlicht. Zu den wichtigsten Erkenntnissen der Mathematik des 19. Jahrhunderts gehört, Funktionen nicht nur punktweise, sondern gleichmäßig über einem ganzen Bereich zu betrachten.
13.1 Fourier-Analyse
Die Zerlegung einer periodischen Funktion in eine Summe von Sinusund Kosinustermen bezeichnet man als Fourier-Analyse. Im Rahmen einer solchen Analyse wird sichtbar, welche Schwingungsanteile die periodische Funktion besitzt.
13.1.1 Periodische Funktionen
Periodische Funktionen haben wir bereits in Abschnitt 5.3.2 betrachtet. Im Zusammenhang mit Fourier-Reihen werden oft zeitabhängige Vorgänge betrachtet. Deshalb verwenden wir in diesem Kapitel für die unabhängige Variable die Notation t. Dabei wird die Periode T oft auch als Schwingungsdauer bezeichnet. Die für Anwendungen in Naturwissenschaften und Technik wichtigen Begri e Periode T und Kreisfrequenz ω wollen wir uns an ein paar einfachen Beispielen veranschaulichen.

530 |
13 Fourier-Reihen |
Beispiel 13.1 (Rechteckfunktion)
Der Prototyp einer periodischen Funktion, die auf dem Intervall (−1, 0] den Wert −1 und auf dem Intervall (0, 1] den Wert 1 hat, ist definiert durch die Darstellung
f |
t |
1 |
für |
1 |
t |
≤ |
0 |
−1 |
für |
−0 |
< t |
1 . |
|||
|
( |
) = œ |
|
|
< |
≤ |
|
|
|
f (t) |
|
|
|
|
|
|
1 |
|
|
|
|
−2 |
−1 |
1 |
2 |
3 |
4 |
t |
|
|
−1 |
|
|
|
|
Die periodische Fortsetzung f |
|
t |
|
2 |
|
f |
t erzeugt eine periodische Funktion mit Periode T |
|
|
2 |
|||||||||||||||||||
und Kreisfrequenz ω |
|
π, die für alle reellen Zahlen definiert ist. Rechteckfunktionen sind vor |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
( |
|
+ |
|
|
) = |
|
( ) |
|
|
|
|
|
|
|
|
|
|
= |
|
|
allem in der Signalverarbeitung von großer Bedeutung. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
Beispiel 13.2 (Sägezahnfunktion) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Wir betrachten den Funktionsprototyp f t |
t auf |
|
|
|
|
f(t) |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
dem Intervall |
|
π, π . Durch |
die |
|
periodische |
Fort- |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
f |
t |
2 π |
f |
t |
|
|
|
|
|
|
|
|
|
( ) = |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
setzung |
|
entsteht |
|
eine |
periodische |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
(− |
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Funktion |
mit |
Periode |
|
T 2 π |
und |
Kreisfrequenz |
|
|
|
|
|
|
|
|
|
t |
|
||||||||||||
|
−2π |
−π |
π 2π 3π 4π |
|
|||||||||||||||||||||||||
|
|
( + ) = ( ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ω 1, die für alle reellen Zahlen definiert ist. In der |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
Elektrotechnik bezeichnet man Sägezahnfunktionen |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
als Kippschwingungen. Sie treten bei Ladevorgängen |
|
|
|
|
|
|
|
|
|
|
|
Ì |
|||||||||||||||||
auf, bei denen auf eine langsame Aufladung eine sehr schnelle Entladung erfolgt. |
|
|
|||||||||||||||||||||||||||
Die Rechteckfunktion aus Beispiel 13.1 und die Sägezahnfunktion aus Beispiel 13.2 verlaufen über die Zeit gemittelt gleich lange oberhalb und unterhalb der t-Achse. Dabei sind die Flächenstücke, die die Funktion oberhalb der t-Achse und unterhalb der t-Achse jeweils mit der t-Achse einschließen, gleich groß. Nicht alle periodischen Funktionen verlaufen auf diese Art symmetrisch zur t-Achse. Eine Verschiebung der Funktion kann mithilfe des Mittelwerts m aus Definition 7.5 bestimmt werden. Dazu definiert man bei einer periodischen Funktion das Verhältnis aus vorzeichenbehaftetem Flächeninhalt über eine volle Periode und der Periode selbst als Mittelwert.
Definition 13.1 (Mittelwert einer periodischen Funktion)
Bei einer Funktion f mit Periode T bezeichnet man das Verhältnis aus dem Integral über eine volle Periode und der Periode selbst
m = |
Integral über eine Periode |
1 |
T |
f(t) dt |
|||
2 |
|||||||
|
|
|
|
S |
|||
Periode |
= T |
||||||
− T2 |
|||||||
als Mittelwert oder Gleichanteil.
Da die Funktion periodisch ist, kann man das Integrationsintervall in Definition 13.1 beliebig wählen, sofern es sich über eine komplette Periode erstreckt.
13.1 Fourier-Analyse |
531 |
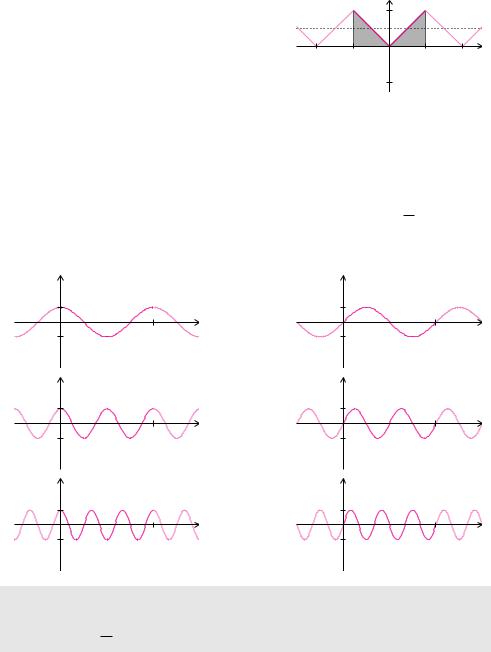
Beispiel 13.3 (Dreieckfunktion)
Der Funktionsprototyp f(t) = StS auf dem Intervall (−π, π] erzeugt durch die periodische Fortsetzung f(t + 2 π) = f(t) eine Funktion mit Periode T = 2 π und Kreisfrequenz ω = 1. Der Mittelwert ergibt sich aus dem Verhältnis von Fläche zu Periode zu
|
1 |
|
π |
1 |
|
2 |
|
π |
|||
m = |
S |
−π f(t) dt = |
π |
= |
|||||||
2 π |
2 π |
|
2 . |
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
π |
f (t) |
|
|
−2π |
−π |
π |
2π |
t |
|
−π |
|
|
|
Die Dreieckfunktion wird in der Signalverarbeitung zur Darstellung von Signalverläufen verwendet. In der Technik verwendet man Dreieckfunktionen für Filter. Ì
13.1.2 Trigonometrische Polynome
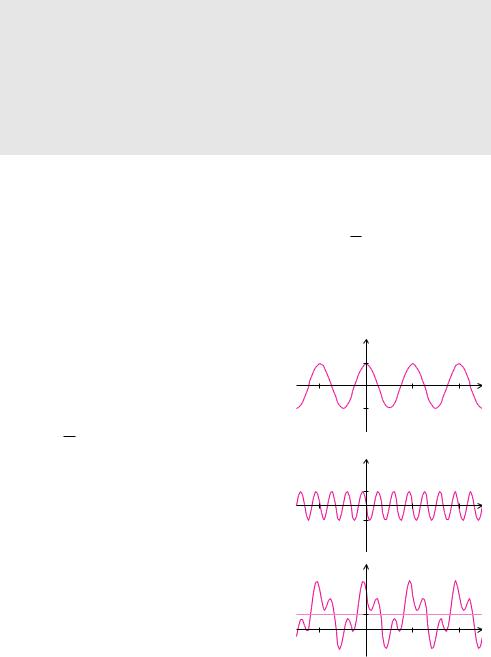
Die Funktionen cos (ω t) und sin (ω t) haben die kleinste Periode T = 2ωπ . Die kleinste Periode der Funktionen cos (2 ω t) und sin (2 ω t) ist zwar T2 , trotzdem sind auch diese Funktionen periodisch mit der Periode T . Auch die Funktionen cos (3 ω t) und sin (3 ω t) sind periodisch mit der Periode T .
1 |
cos(ω t) |
|
|
|
|
−1 |
T |
t |
|
|
1 |
cos(2 ω t) |
|
|
|
|
−1 |
T |
t |
|
|
1 |
cos(3 ω t) |
|
|
|
|
−1 |
T |
t |
|
|
1 |
sin(ω t) |
|
|
|
|
−1 |
T |
t |
|
|
1 |
sin(2 ω t) |
|
|
|
|
−1 |
T |
t |
|
|
1 |
sin(3 ω t) |
|
|
|
|
−1 |
T |
t |
|
|
Periode von sin (k ω t) und cos (k ω t)
Die Funktionen sin (k ω t) und cos (k ω t) sind für jede natürliche Zahl k periodisch mit der Periode T = 2ωπ .
Die Überlagerung von Funktionen mit derselben Periode T erzeugt eine Funktion mit der Periode T . Dieses Prinzip wendet man auf die Funktionen cos(k ω t) und sin(k ω t) an.
532 |
13 Fourier-Reihen |
Definition 13.2 (Trigonometrisches Polynom)
Eine Funktion pn mit Periode T , die man in der Form
|
a0 |
n |
|
|
2 π |
|
|
pn(t) = |
+ kQ1 |
(ak cos (k ω t) + bk sin (k ω t)) , |
ω = |
, |
|||
2 |
T |
||||||
|
|
= |
|
|
|
|
darstellen kann, nennt man ein trigonometrisches Polynom vom Grad n. Die Ko- e zienten a0, a1, a2, . . ., an und b1, b2, . . ., bn sind dabei beliebige Zahlen, wobei allerdings einer der beiden höchsten Koe zienten an oder bn nicht null sein darf.
Die Definition hat auf den ersten Blick einen kleinen Schönheitsfehler. Warum gibt es einen Koe zienten a0 und keinen Koe zienten b0? Der Grund dafür ist nahe liegend. Für k = 0 ergibt cos(0 ω t) den konstanten Wert 1, hingegen ist sin(0 ω t) null.
Für den Mittelwert eines trigonometrischen Polynoms gilt m = a20 , denn die Integrale der Funktionen cos(k ω t) und sin(k ω t) über eine komplette Periode ergeben jeweils null. Die Skalierung des Koe zienten a0 mit dem Faktor 12 scheint an dieser Stelle willkürlich zu sein. In Abschnitt 13.2.2 werden wir zur komplexen Schreibweise übergehen. Dabei wird genau diese Skalierung zu einfacheren Formeln führen.
Beispiel 13.4 (Trigonometrisches Polynom)
Die Funktion
p3(t) = 2 + 3 cos (t) − 2 sin (3t)
stellt ein trigonometrisches Polynom vom Grad n = 3 dar. Der Mittelwert ist
m = a0 = 2.
2
Bei den Kosinusgliedern ist
a1 = 3, a2 = 0, a3 = 0
und bei den Sinusgliedern ist
|
|
b1 = 0, b2 = 0, b3 = −2. |
|||||
Aus der |
Überlagerung |
der beiden Schwingungen |
|||||
3 cos |
t |
) |
und |
− |
2 sin 3t |
) |
entsteht unter Berücksich- |
|
( |
|
( |
|
|||
tigung einer Verschiebung um den Mittelwert m = 2 parallel zur t-Achse die Funktion p3 mit Periode
T = 2 π.
|
3 |
3 cos (t) |
|
|
|
|
|
|
|
−2π |
-3 |
2π |
4π |
t |
|
|
|
|
|
|
2 |
−2 sin (3 t) |
|
|
|
|
|
|
|
−2π |
-2 |
2π |
4π |
t |
|
|
p3(t) |
|
|
|
2 |
|
|
|
−2π |
|
2π |
4π |
t |
Ì
Bei trigonometrischen Polynomen wird der Begri Grad anders verwendet, als wir das bisher gewohnt sind. Im Gegensatz zu herkömmlichen Polynomen bezieht sich der Begri Grad nicht auf die höchste Potenz, sondern auf das höchste ganzzahlige Vielfache der
