
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

460 |
12 Gewöhnliche Di erenzialgleichungen |
In manchen Fällen ist es kompliziert oder sogar unmöglich, die allgemeine Lösung einer Di erenzialgleichung zu bestimmen. Dann ist man auf andere Lösungsmethoden für Anfangsund Randwertprobleme angewiesen. Oft verwendet man in solchen Fällen numerische Verfahren zur Bestimmung einer Näherungslösung. Diese Verfahren betrachten wir in Abschnitt 12.6.
Während eine Di erenzialgleichung der Ordnung n zusammen mit n Anfangswerten in aller Regel eindeutig lösbar ist, ist dies bei n Randwerten oftmals nicht der Fall.
Beispiel 12.8 (Randwertprobleme ohne eindeutige Lösung)
a) Die Di erenzialgleichung des Randwertproblems
y′′ + 9y = 0, y(0) = 1, y(π) = 0
hat die allgemeine Lösung y(x) = C1 sin (3x) + C2 cos (3x). Aus dem ersten Randwert ergibt sich C2 = 1. Damit ist y(π) = −1, unabhängig von der Konstanten C2. Die zweite Randbedingung ist nicht erfüllbar. Dieses Randwertproblem besitzt also keine Lösung.
b) Betrachtet man dagegen das Randwertproblem
y′′ |
9y 0, y 0 1, y |
π |
1, |
|
|
|
|
|
so sind+alle=Funktionen( ) =der Form( |
)y=x− |
C1 sin |
3x |
cos |
3x |
Lösungen. Dieses Randwert- |
||
problem besitzt also unendlich |
viele Lösungen. |
( ) + |
( |
) |
Ì |
|||
|
( ) = |
|
||||||
Definition 12.7 (Partikuläre Lösung)
Eine einzelne Lösungsfunktion einer gewöhnlichen Di erenzialgleichung nennt man spezielle Lösung oder partikuläre Lösung.
In der Theorie der Di erenzialgleichungen gibt es Sätze, die darüber Auskunft geben, unter welchen Bedingungen ein Anfangswertoder Randwertproblem überhaupt lösbar ist und ob es im Falle der Lösbarkeit eine eindeutige Lösung gibt. Dazu wird neben der üblichen Stetigkeit von Funktionen die nach Rudolf Otto Sigismund Lipschitz benannte Lipschitz-Stetigkeit verwendet, siehe [Heuser:DGL].
12.1.3 Richtungsfeld und Orthogonaltrajektorie
Wir betrachten in diesem Abschnitt Di erenzialgleichungen erster Ordnung in expliziter Form
y′ = f(x, y).
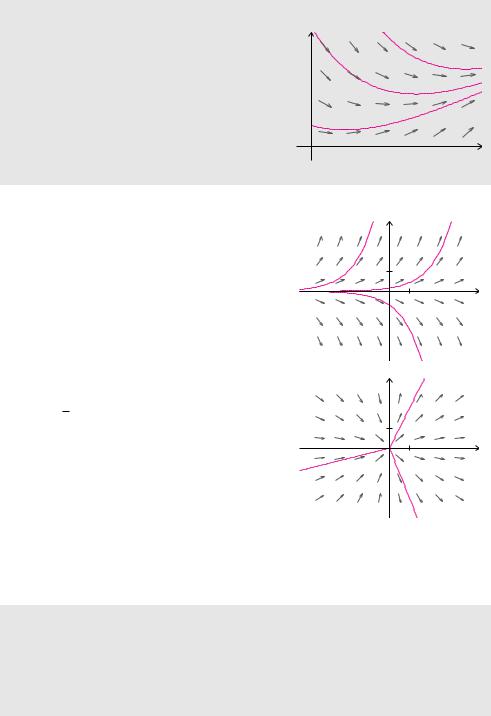
An jeder Stelle (x, y), an der die rechte Seite der Di erenzialgleichung definiert ist, wird durch die Di erenzialgleichung eine Steigung festgelegt. Wenn wir nun in entsprechend vielen Punkten diese Tangentenrichtungen grafisch veranschaulichen, dann lässt sich der Verlauf der Lösungen erkennen. Lösungsfunktionen verlaufen nämlich immer tangential zu diesen Richtungen. Besonders elegant kann man diese sogenannten Richtungsfelder mit Computerprogrammen erzeugen.
12.1 Einführung |
461 |
Definition 12.8 (Linienelement und Richtungsfeld)
Eine Di erenzialgleichung erster Ordnung in expliziter Form
y′ = f(x, y)
ordnet jedem Punkt in der Ebene eine Steigung zu. Den zu einer Steigung gehörenden Richtungsvektor nennt man auch Linienelement. Die Menge aller Linienelemente heißt Richtungsfeld der Di erenzialgleichung.
y |
x |
Beispiel 12.9 (Richtungsfeld)
a) Das Richtungsfeld der Di erenzialgleichung
y′ = y
ist für alle Punkte in der (x, y)-Ebene definiert. Es ist symmetrisch zur x-Achse. Alle Linienelemente durch Punkte mit demselben y-Wert haben dieselbe Steigung. Die Lösungsfunktionen y(x) = C ex verlaufen tangential zum Richtungsfeld.
b) Das Richtungsfeld der Di erenzialgleichung
y′ = y x
besteht aus Linienelementen, die in Richtung der Ursprungsgeraden verlaufen. Auf der y-Achse, also für x = 0, sind formal keine Linienelemente definiert. Abgesehen vom Ursprung besitzen die Linienelemente auf der y-Achse im Grenzwert die Steigung ±∞. Im Ursprung ist keine Steigung definiert. Man bezeichnet diesen Punkt als Singularität der Di erenzialgleichung. Dem Richtungsfeld kann man entnehmen, dass die Lösungsfunktionen Halbgeraden bis zum Ursprung sind.
y |
|
1 |
|
1 |
x |
y |
|
1 |
|
1 |
x |
Ì
Lösungen im Richtungsfeld, Singularitäten
Die Lösungen einer Di erenzialgleichung verlaufen tangential zum Richtungsfeld. Durch Punkte, in denen das Richtungsfeld eindeutig definiert ist, verläuft genau eine Lösung. Verschiedene Lösungen der Di erenzialgleichung können sich nur in Punkten schneiden, in denen das Richtungsfeld nicht eindeutig definiert ist. Solche Punkte bezeichnet man als Singularitäten oder Gleichgewichtspunkte.
462 |
12 Gewöhnliche Di erenzialgleichungen |
Bei Stabilitätsuntersuchungen in Abschnitt 12.5.5 werden wir Gleichgewichtspunkte nochmals genauer betrachten.
Nun kann man an jeder Stelle die zur Steigung der Di erenzialgleichung senkrechte Steigung betrachten. So gelangt man zur Di erenzialgleichung der Orthogonaltrajektorien.
Definition 12.9 (Di erenzialgleichung der Orthogonaltrajektorien)
Ersetzt man in einer Di erenzialgleichung erster Ordnung die Steigung durch den negativen Kehrwert, so bezeichnet man diese neue Di erenzialgleichung als Di erenzialgleichung der Orthogonaltrajektorien.
Beispiel 12.10 (Orthogonaltrajektorie) |
|
|
|
|||||
Die Linienelemente der Di erenzialgleichung |
y |
|
||||||
|
|
x |
|
|
|
|
|
|
|
|
y′ = − y |
|
|
|
|
1 |
|
stehen senkrecht auf den Linienelementen der Di e- |
|
|
||||||
renzialgleichung y′ |
|
y |
. Das Richtungsfeld |
besteht |
1 |
x |
||
|
x |
|||||||
aus |
Linienelementen, |
die orthogonal zu |
den Ur- |
|
|
|||
|
= |
|
|
|
|
|
||
sprungsgeraden verlaufen. Auf der x-Achse, also für |
|
|
||||||
y |
= |
0, sind formal |
keine Linienelemente definiert. |
|
|
|||
Dem Richtungsfeld kann man entnehmen, dass die |
|
Ì |
||||||
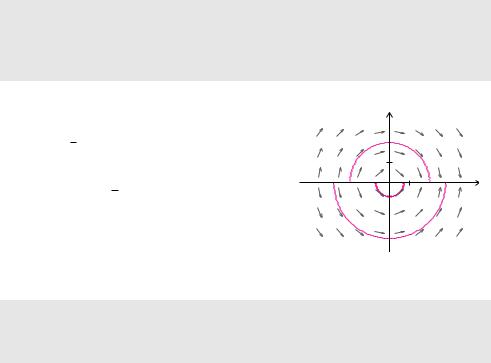
Lösungsfunktionen Kreise um den Ursprung sind. |
|
|||||||
Orthogonaltrajektorien
Alle Lösungsfunktionen der ursprünglichen Di erenzialgleichung und der zugehörigen Di erenzialgleichung der Orthogonaltrajektorien stehen überall senkrecht zueinander.
12.1.4 Di erenzialgleichung und Funktionenschar
Die allgemeine Lösung einer Di erenzialgleichung besteht in der Regel aus unendlich vielen Lösungsfunktionen, die mehr oder weniger ähnliches Verhalten aufweisen. Solche Funktionen lassen sich oftmals als Funktionenschar beschreiben. Nun kann man sich umgekehrt die Frage stellen, wie man zu einer gegebenen Funktionenschar eine Di erenzialgleichung herleiten kann, die diese Funktionenschar als Lösung hat.
Beispiel 12.11 (Di erenzialgleichung der Exponentialfunktion)
Die Exponentialfunktionen
y |
x |
) = |
C e−2 x, C |
|
R |
( |
|
|
|
beschreiben eine Funktionenschar mit dem Scharparameter C. Wir suchen eine Di erenzialgleichung, die genau diese Funktionen als allgemeine Lösung besitzt. Die Ableitung
y′(x) = −2 C e−2 x

12.2 Di erenzialgleichungen erster Ordnung |
463 |
ist noch nicht unsere gesuchte Di erenzialgleichung, denn diese Gleichung enthält immer noch den Parameter C. Diese Gleichung stellt eine Schar von Di erenzialgleichungen dar und nicht eine einzige Di erenzialgleichung. Wenn wir jedoch die Gleichung von y(x) und von y′(x) nach C auflösen und gleichsetzen
C |
|
y |
|
x |
|
e2 x |
, C |
1 |
|
|
x |
|
e2 x |
|
y |
x |
|
e2 x |
1 |
x e2 x |
, |
||||
|
|
|
|
2 y′ |
|
|
|
|
|
2 y′ |
|||||||||||||||
|
= |
|
( |
|
) |
|
|
= − |
|
|
( |
|
) |
|
Ô |
y( |
|
) |
|
y |
= − |
|
|
( ) |
Ì |
dann ergibt sich die gesuchte Di erenzialgleichung |
′ = −2 |
|
. |
|
|
|
|||||||||||||||||||
Mit der Vorgehensweise aus Beispiel 12.11 lässt sich in der Regel zu einer gegebenen Funktionenschar eine Di erenzialgleichung bestimmen, die genau diese Funktionenschar als allgemeine Lösung besitzt.
Di erenzialgleichung einer Funktionenschar
Wenn man diejenige Di erenzialgleichung bestimmen möchte, die eine bestimmte Funktionenschar als Lösung hat, dann kann man folgendermaßen vorgehen:
(1)Bestimme die Ableitung der Funktionsgleichung der Funktionenschar.
(2)Eliminiere den Scharparameter.
Beispiel 12.12 (Di erenzialgleichung der Ursprungskreise)
Die Ursprungskreise
x2 + y2 = r2, r > 0
beschreiben eine Funktionenschar mit dem Scharparameter r. Mithilfe der Methode des impliziten Di erenzierens, siehe Abschnitt 6.2.4,
2 x + 2 y y′ = 0 |
Ô y′ |
= − |
x |
|
y |
|
|||
erhalten wir eine Di erenzialgleichung, deren allgemeine Lösung aus den Ursprungskreisen besteht, vergleiche Beispiel 12.10. Ì
12.2 Di erenzialgleichungen erster Ordnung
Bei den meisten Di erenzialgleichungen erster Ordnung kann man die allgemeine Lösung durch Separation ermitteln. Separation der Variablen ist ein Lösungsverfahren, das sich direkt anwenden lässt oder manchmal nach einer geeigneten Substitution zum Erfolg führt. Wir werden zwei unterschiedliche Substitutionen, nämlich die lineare Substitution und die Ähnlichkeitssubstitution, in Betracht ziehen. Es gibt noch zahlreiche weitere Verfahren zur Lösung spezieller Typen von Di erenzialgleichungen, die alleine ein Buch füllen würden. Trotzdem sei an dieser Stelle ausdrücklich darauf hingewiesen, dass bis heute für viele Di erenzialgleichungen keine expliziten Lösungen bekannt sind.
