12.6 Numerische Verfahren

Man spricht zwar von numerischen Lösungsverfahren für gewöhnliche Di erenzialgleichungen, genau genommen meint man aber numerische Verfahren zur Lösung von Anfangswertproblemen. Man sucht die Lösung einer Di erenzialgleichung oder eines Di erenzialgleichungssystems, die zu einem bestimmten Anfangszeitpunkt einen vorgegebenen Anfangswert hat. Außerdem benötigen numerische Verfahren für alle Größen in der Di e- renzialgleichung konkrete Werte. Abhängigkeiten der Lösung von Parameterwerten lassen sich mit numerischen Verfahren nicht unmittelbar erkennen. Ein numerisches Verfahren liefert als Lösung eines Anfangswertproblems eine Folge von Näherungswerten. In der Praxis fordert man, dass diese Näherungswerte bis auf eine vorgegebene Toleranz mit der mathematisch exakten Lösung übereinstimmen.

12.6.1 Polygonzugverfahren von Euler

Die von Leonhard Euler bereits im Jahre 1768 verö entlichte Methode ist das einfachste Verfahren zur numerischen Lösung von Anfangswertproblemen. Trotzdem oder gerade deshalb wird es heute zur numerischen Lösung praktischer Probleme an vielen Stellen eingesetzt. Wir betrachten zunächst eine gewöhnliche Di erenzialgleichung erster Ordnung mit einem Anfangswert zur Zeit t0:

x˙ = f(x, t), x(t0) = x0.

Die Kernidee des Verfahrens ist, einen Näherungswert für die gesuchte Lösung zum Zeitpunkt t1 = t0 + h zu bestimmen. Dabei ist h die sogenannte Schrittweite des Verfahrens. Die Kunst in der Numerik besteht darin, einen möglichst optimalen Wert für die Schrittweite zu wählen. Je größer man die Schrittweite wählt, um so größer wird der Unterschied zwischen Näherungswert und exakter Lösung. Wählt man die Schrittweite sehr klein, dann sind sehr viele Schritte erforderlich, um die Lösung über einem bestimmten Intervall anzunähern. Außerdem kommt es bei sehr kleinen Schrittweiten zu Problemen mit der Rechengenauigkeit. Es liegt hier dieselbe Problematik wie beim numerischen Di erenzieren vor, siehe Abschnitt 6.5.1.

Wenn wir die Ableitung von x an der Stelle t0 durch den Vorwärtsdi erenzenquotienten annähern, ergibt sich

x˙(t0) ≈ x(t0 + h) − x(t0) . h

Diese Beziehung in die Di erenzialgleichung eingesetzt liefert:

Damit können wir einen Näherungswert x˜1 für die exakte Lösung x(t1) berechnen:

x(t0 + h) = x(t1) ≈ x˜1 = x0 + h f(x0, t0).

Im Folgenden verwenden wir für Näherungswerte stets das Symbol ˜. Das Verfahren kann man nun mehrmals wiederholen. Dabei verwenden wir in jedem Schritt dieselbe Schrittweite h. Bei der Lösung praktischer Probleme wird üblicherweise die Schrittweite h in jedem Schritt angepasst. Weitere Einzelheiten dazu findet man bei [Höllig].

Definition 12.33 (Polygonzugverfahren von Euler)

Mit dem Polygonzugverfahren von Euler kann man für das Anfangswertproblem

x˙ = f(x, t), x(t0) = x0

mit der Iterationsvorschrift

x˜0 = x0, x˜k+1 = x˜k + h f(x˜k, tk), tk+1 = tk + h, k = 0, 1, 2, . . .

Schritt für Schritt Näherungswerte x˜k für die exakte Lösung x(t0 + k h) berechnen. Dabei beeinflusst die gewählte Schrittweite h den Fehler der Näherungswerte.

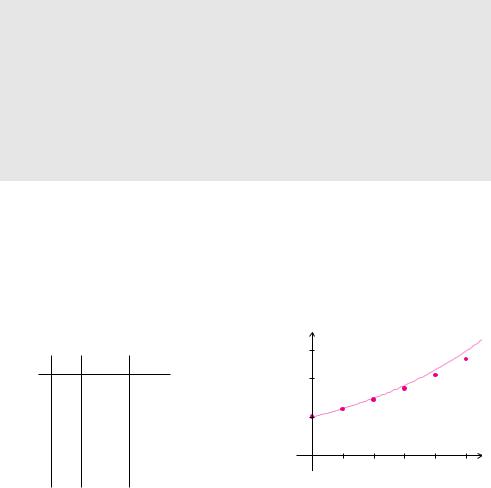
Beispiel 12.50 (Polygonzugverfahren von Euler)

Wir betrachten das Polygonzugverfahren von Euler für das Anfangswertproblem

x˙ = x, x(0) = 1, t [0, 1].

Da wir bei dieser Di erenzialgleichung die exakte Lösung x(t) = et kennen, können wir die Qualität unserer Näherungslösungen beurteilen. Die Näherungslösungen berechnen sich aus

x˜k+1 = x˜k + h x˜k, k = 0, 1, 2, . . .

Ì

In Beispiel 12.50 erkennt man ein typisches Verhalten von numerischen Näherungsverfahren für Anfangswertprobleme. Die Abweichung der Näherungslösung von der exakten Lösung nach dem ersten Schritt, der sogenannte lokale Fehler, ist noch verhältnismäßig gering. Der globale Fehler, also die maximale Abweichung, die sich über das gesamte Intervall ergibt, ist deutlich größer als der lokale Fehler.

12.6.2 Euler-Verfahren für Di erenzialgleichungssysteme

Das Polygonzugverfahren von Euler lässt sich auch auf Anfangswertprobleme mit Di e- renzialgleichungssystemen übertragen, allerdings nur auf Systeme erster Ordnung. Das stellt jedoch keine wesentliche Einschränkung dar, denn Di erenzialgleichungen oder Differenzialgleichungssysteme höherer Ordnung können wir durch Zustandsvariablen immer in äquivalente Systeme erster Ordnung überführen, siehe Abschnitt 12.5.2. Die Methode zeigen wir anhand eines Beispiels.

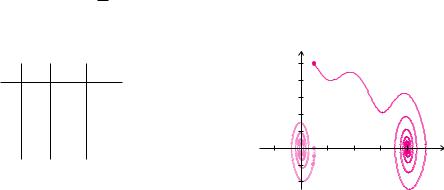
Beispiel 12.51 (Euler-Verfahren für das Pendel)

Ein Pendel wird durch das nichtlineare Di erenzialgleichungssystem erster Ordnung

beschrieben, siehe Abschnitt 12.7.5 und Beispiel 12.39. Dabei verwenden wir für die beiden Zustandsgrößen die Bezeichnungen x und y. Wir wenden das Polygonzugverfahren von Euler auf beide Zustände an:

Mit den konkreten Werten m = 1 kg, l = 1 m, g = 10 sm2 , k = 12 , t0 = 0, x(0) = π2 , y(0) = 0 und der Schrittweite h = 0.1 erhalten wir folgende Näherungswerte:

Das Polygonzugverfahren von Euler ist ein sehr einfaches Verfahren zur Integration von Di erenzialgleichungen. In der Literatur gibt es aufwendigere Einschrittverfahren oder auch Mehrschrittverfahren, siehe [Mohr:Numerik], [Schwarz] oder [Stoer-Bulirsch]. Diese Verfahren haben alle das Ziel, mit möglichst wenigen Rechenschritten ein möglichst genaues Ergebnis zu liefern. Ein populäres und oft eingesetztes Einschrittverfahren ist das sogenannte Runge-Kutta-Verfahren, benannt nach Carl Runge und Martin Wilhelm Kutta. Eine weitere Idee zur numerischen Lösung von Di erenzialgleichungen ist die auf den norwegischen Mathematiker Marius Sophus Lie zurückgehende Nutzung kontinuierlicher Symmetrien bei der Integration.