
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
295
7 Integralrechnung
Die Einstiegsfrage in die Integralrechnung betri t das sogenannte Flächenproblem: Wie kann man den Flächeninhalt unter einer Funktion berechnen? Wie so oft in der Mathematik liegt der Schlüssel zur Lösung des Problems darin, den geeigneten Querbezug herzustellen. Die wesentliche Erkenntnis dieses Kapitels ist der Zusammenhang der Differenzialrechnung mit dem Flächenproblem. Wir werden sehen, dass die Integralrechnung eine Art Umkehrung der Di erenzialrechnung darstellt.
7.1 Flächenproblem
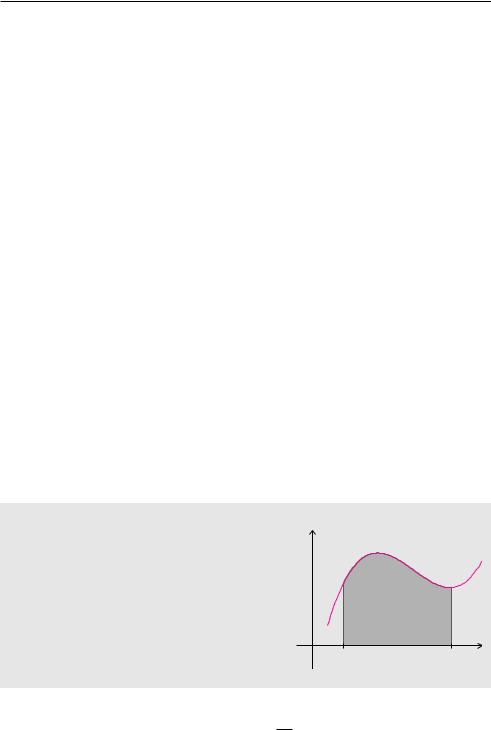
Zunächst beschränken wir uns nur auf Funktionen, die keine negativen Funktionswerte haben und stetig sind. Das Schaubild einer solchen Funktion schließt im Intervall [a, b] mit der x-Achse eine Fläche A ein. Wir suchen nach einer Methode, diesen Flächeninhalt zu berechnen.
7.1.1 Integralsymbol
Die Fläche ist erst durch Angabe von Untergrenze a und Obergrenze b eindeutig festgelegt. Wir benötigen deshalb eine geeignete Schreibweise, um unmissverständlich klar zu machen, in welchem Bereich wir die Funktion f betrachten.
Definition 7.1 (Integralsymbol)
Eine stetige und nicht negative Funktion f begrenzt für x-Werte zwischen a und b mit der x-Achse ein Flächenstück. Für den Inhalt A dieser Fläche verwendet man die Schreibweise mit dem Integralsymbol
A = Sa |
b |
f(x) dx. |
Die Funktion f unter dem Integral bezeichnet man als Integrand.
y |
f(x) |
|
|
|
|
|
Zab f(x) dx |
|
a |
b |
x |
Wir verwenden die Sprechweise „Integral von a bis b über f von x dx“. Die Bezeichnung
dx kennen wir bereits von der Ableitung f′(x) = df . dx
296 |
7 Integralrechnung |
Beim Integral setzen wir zunächst f ≥ 0 und a ≤ b voraus. Im weiteren Verlauf dieses Kapitels werden wir jedoch sehen, dass Integrale auch für f < 0 und a > b sinnvoll definiert werden können. Integrale, bei denen ∞ oder −∞ als Grenzen vorkommen, bezeichnet man als uneigentliche Integrale. Die Besonderheiten solcher Integrale werden in Abschnitt 7.3.5 beleuchtet.
Das Integralsymbol ∫ wurde in Anlehnung an ein langgezogenes „S“ als Anfangsbuchstabe des lateinischen Worts „summa“ bereits im 17. Jahrhundert von dem Mathematiker Gottfried Wilhelm von Leibniz eingeführt. Bei der Definition des Integralsymbols fungiert die Variable x lediglich als Platzhalter. Wir können anstatt x jede beliebige Variable verwenden, mit den Worten von Goethes Faust formuliert: „Name ist Schall und Rauch“.
Integrationsvariable
Die Bezeichnung der Integrationsvariable spielt keine Rolle:
b |
b |
f(t) dt = Sa |
b |
Sa |
f(x) dx = Sa |
f(u) du = . . . |
7.1.2 Integral als Grenzwert von Summen
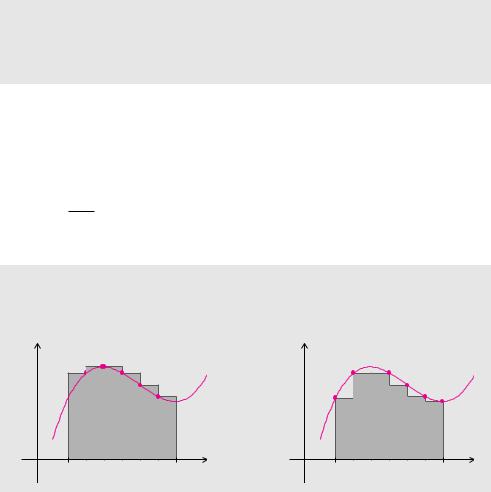
Eine nahe liegende Idee bei der Berechnung einer Fläche unter einer Funktion ist die Verwendung kleiner Rechtecke. Dazu unterteilt man das Intervall von a bis b in n gleich große Teilintervalle. Bei dieser sogenannten äquidistanten Unterteilung hat jedes Teilintervall die
Länge x = b − a. Rechtecke, deren Höhen so gewählt werden, dass sie gerade noch unter n
die Funktion passen, erzeugen die sogenannte Untersumme. Bei der Obersumme entsprechen die Höhen der Rechtecke den maximalen Funktionswerten.
Unterund Obersumme
Die Fläche unter einer stetigen und nicht negativen Funktion kann durch Untersumme und Obersumme angenähert werden. Der tatsächliche Wert der Fläche ist sicherlich nicht kleiner als die Untersumme und sicherlich auch nicht größer als die Obersumme.
y |
f(x) |
n = 6 |
|
|
|
|
|
a |
x |
b |
x |
|
|{z} |
|
|
y |
f(x) |
n = 6 |
|
|
|
|
|
a |
x |
b |
x |
|
|{z} |
|
|
Je kleiner man die Grundseiten der Rechtecke x wählt, um so geringer ist der Unterschied zwischen Unterund Obersumme. Wenn man n groß wählt, kann man die Fläche entsprechend genau berechnen.

7.1 Flächenproblem |
297 |
Beispiel 7.1 (Unterund Obersumme)
Die Fläche unter der Funktion f(x) = ln x für x-Werte zwischen 2 und 6 soll mithilfe von Unterund Obersumme näherungsweise berechnet werden.
y |
|
|
|
|
|
|
2 |
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
x |
y |
|
|
|
|
|
|
2 |
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
x |
Eine grobe Abschätzung erhält man mit n |
= |
4 Rechtecken, deren Grundseiten die Länge x |
= |
1 |
haben. Die Untersumme ergibt |
|
|
SU = 1 ln 2 + 1 ln 3 + 1 ln 4 + 1 ln 5 = ln(2 3 4 5) = ln 120 ≈ 4.7875
und die Obersumme
SO = 1 ln 3 + 1 ln 4 + 1 ln 5 + 1 ln 6 = ln(3 4 5 6) = ln 360 ≈ 5.8861.
Der Wert des bestimmten Integrals muss zwischen den beiden berechneten Werten liegen, also
4.7875 ≈ ln 120 ≤ 2 |
6 |
ln x dx ≤ ln 360 ≈ 5.8861. |
|
Für Problemstellungen ausS |
der Praxis ist diese Abschätzung natürlich zu grob. Allerdings lässt |
sich die prinzipielle Vorgehensweise zu einem praktikablen numerischen Verfahren erweitern, siehe
Abschnitt 7.5.1. Ì
Die Grundseiten der Rechtecke müssen keinesfalls alle gleich groß sein. Wir können Rechtecke mit beliebigen Grundseiten xk verwenden. Anstelle von minimalen und maximalen Funktionswerten können wir die Höhe der Rechtecke durch Funktionswerte f(xk) an einer beliebigen Stelle xk im Rechteck festlegen.
Wenn wir die Grundseiten der Rechtecke nun immer kleiner werden lassen, dann wird der Näherungswert der Fläche immer genauer. Somit können wir die Fläche unter einer Funktion mathematisch exakt als einen Grenzwert von Summen definieren.
Fläche als Grenzwert von Summen
Die Fläche unter einer stetigen und nicht negativen Funktion f entspricht dem Grenzwert von Summen
|
b |
( |
|
) d |
|
n |
|
|
|
|
f |
x |
x |
lim |
f |
x |
xk, |
||
S |
a |
|
|
= n→∞ kQ1 |
|
( k) |
|||
|
|
|
|
|
= |
|
|
|
|
falls die Grundseiten der Rechtecke |
xk gegen |
||||||||
null streben und der Grenzwert der Rechtecksummen existiert. Dabei ist xk eine Stelle innerhalb des Rechtecks mit Grundseite xk.
y |
f(xk) |
|
|
|
|
a |
b |
x |
|
xk |
|
|
|{z} |
|

298 |
7 Integralrechnung |
7.1.3 Bestimmtes Integral
Bei den bisherigen Betrachtungen sind wir stets davon ausgegangen, dass die Funktion stetig ist und keine negativen Funktionswerte hat. Die Grenzwertformel ist jedoch auch für unstetige Funktionen oder Funktionen mit negativen Funktionswerten gültig. Somit können wir mithilfe der Grenzwertdarstellung das Integral für beliebige Funktionen definieren.
Definition 7.2 (Bestimmtes Integral)
Das bestimmte Integral einer Funktion f zwischen den Grenzen a und b ist definiert durch den Grenzwert der Summen
bn
|
f |
( |
x |
) d |
x |
lim |
f |
x |
x , |
S |
a |
|
|
= n→∞ kQ1 |
|
( k) |
k |
||
|
|
|
|
|
= |
|
|
|
wobei xk die Grundseiten der Rechtecke und xk jeweils eine Stelle innerhalb der Rechtecke bezeichnet.
Für beliebige Funktionen ist nicht sichergestellt, dass der Grenzwert existiert. Man kann jedoch zeigen, dass der Grenzwert für stetige und sogar für stückweise stetige Funktionen immer existiert. Integrale über Funktionen, die zwischen a und b Definitionslücken haben, werden wir in Abschnitt 7.3.5 noch genauer untersuchen.
Bei negativen Funktionswerten ist das Produkt aus Grundseite xk und Funktionswert f(xk) negativ. Somit erzeugen negative Funktionswerte Flächenanteile, die negativ gezählt werden. Bei einer nicht negativen Funktion stimmt die Fläche A, die die Funktion zwischen a und b mit der x-Achse einschließt, mit dem bestimmten Integral überein. Die Flächenberechnung im Fall von negativen Funktionswerten werden wir in Abschnitt 7.4.1 genauer beleuchten.
Für viele praktische Zwecke ist die Definition eines Integrals als Grenzwert von Summen völlig ausreichend. Diese Definition geht im Wesentlichen auf Georg Friedrich Bernhard Riemann zurück. Man bezeichnet dieses Integral daher auch als Riemann-Integral. Henri Lebesgue ist es gelungen, die hier vorgestellte Definition zu verallgemeinern. Das LebesgueIntegral wird mithilfe des sogenannten Lebesgue-Maßes definiert. Die Maßtheorie bildet einen wichtigen Grundpfeiler der Mathematik.
Beispiel 7.2 (Bestimmtes Integral des Sinus)
Für das bestimmte Integral der Funktion f(x) = sin x für x-Werte zwischen 0 und 2π gilt
2π
Ssin x dx = 0.
0
Die positiven Anteile zwischen 0 und π werden durch die negativen Anteile zwischen π und 2π kompensiert.
y |
|
|
f(x) = sin x |
|
|
1 |
|
|
A+ |
|
|
π |
A− |
2π x |
−1 |
|
|
|
|
|
Ì
