
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

387
10 Funktionen mit mehreren Variablen
Bislang haben wir ausschließlich Funktionen betrachtet, die von einer unabhängigen Variablen abhängen. In Anwendungen treten aber häufig Funktionszusammenhänge auf, bei denen der Funktionswert etwa von der Zeit und vom Ort abhängt. Deshalb erweitern wir den Funktionsbegri auf mehrere unabhängige Variable. Je nach Art der Problemstellung hat man so zwei, drei oder noch mehr unabhängige Variable. Wir werden in diesem Kapitel im Wesentlichen Funktionen mit zwei Variablen untersuchen. Die Verallgemeinerung von zwei auf drei und mehr Variable ist an den meisten Stellen ohne neue Gedanken durchführbar.
10.1 Definition und Darstellung
In diesem Abschnitt klären wir, wie man Funktionen mit mehreren Variablen formal definiert. Außerdem erläutern wir Methoden zur grafischen Darstellung. Dazu betrachten wir einfache Beispiele von Funktionen mit zwei Variablen.
10.1.1 Definition einer Funktion mit mehreren Variablen
Bei Funktionen mit mehreren Variablen ist der Definitionsbereich eine Teilmenge des entsprechenden Raumes. So liegt der Definitionsbereich einer Funktion mit zwei Variablen in der Ebene. Jedem Punkt dieses Definitionsbereichs in der Ebene wird dann durch die Funktion ein Funktionswert zugeordnet.
Definition 10.1 (Funktion mit zwei Variablen)
Unter einer Funktion f mit zwei Variablen versteht man eine Abbildung, die jedem Zahlenpaar (x, y) aus einer Definitionsmenge D R2 genau eine reelle Zahl z aus einer Wertemenge W zuordnet:
(x, y) ( z = f(x, y), (x, y) D.
Für drei und mehr unabhängige Variable sind die Schreibweisen
f(x, y, z), f(x1, x2, x3, . . . , xn), f(x)
gebräuchlich. Dabei bezeichnet x = (x1, x2, x3, . . . , xn) einen Vektor.
388 |
10 Funktionen mit mehreren Variablen |
10.1.2 Schaubild einer Funktion mit mehreren Variablen
Das Schaubild von Funktionen mit einer Variablen kann man in der Ebene darstellen. Zur Visualisierung von Funktionen mit zwei Variablen benötigt man eine weitere Dimension. Funktionsschaubilder sind nun Flächen im dreidimensionalen Raum. Hier wird deutlich, dass die grafische Darstellung von Funktionen mit drei und mehr Variablen mindestens einen vierdimensionalen Raum erfordert, was jedoch die menschliche Vorstellungskraft vor große Herausforderungen stellt.
Schaubild
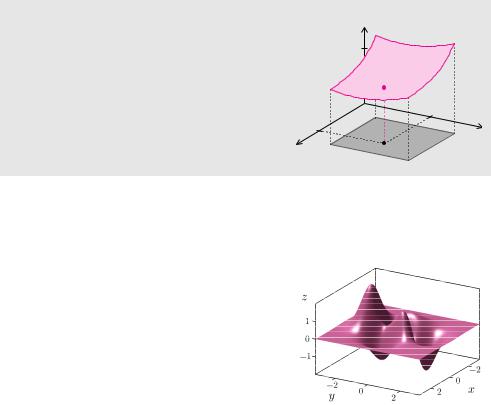
Das Schaubild einer Funktion |
z |
f
z = f(x, y)
ist eine Fläche im Raum. Dabei gibt es zu jedem |
|
f(x0, y0) |
|
||||||||||
|
|
|
|||||||||||
Punkt |
x0, y0 |
|
des Definitionsbereichs D genau |
|
y0 |
y |
|||||||
Punkt z |
f |
|
x |
0 |
, y |
0 |
|
auf der Fläche. |
|
|
|||
einen ( |
|
)0 |
= |
( |
|
|
) |
|
x |
D |
|
||
|
|
|
|
|
|
|
|
|
|
||||
Durch Visualisierungssoftware lassen sich selbst komplexe Funktionen mit zwei Veränderlichen ansprechend darstellen. Zur Erzeugung möglichst realistischer Bilder verwendet man dabei unterschiedliche Methoden der Computergrafik.
Beispiel 10.1 (Peaks)
Die Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x, y |
|
|
1 x 2 e x2 1 y 2 |
|
|
||||||||||||
( ) = |
|
|
3 |
) |
|
5 |
− |
|
|
2 |
|
y |
2 |
||||
|
|
y |
−( −x) |
|
|
||||||||||||
3 x |
|
|
|
|
x e |
|
|
|
|
|
|||||||
( |
|
+ |
|
|
y2 |
|
− |
|
− |
|
|
||||||
|
− |
|
( |
|
|
x |
2 |
|
) |
|
|
|
|||||
|
e |
1 |
|
+ |
|
|
|
− |
|
|
|
|
|
||||
|
− |
|
−( |
− ) − |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
beschreibt eine Fläche im Raum, die aus mehre- |
|
ren e-Funktionen zusammengesetzt ist. Alle beteilig- |
|
ten e-Funktionen haben negative Exponenten, sodass |
|
die Funktionswerte, mit zunehmender Entfernung der |
|
x-Werte und y-Werte vom Ursprung schnell gegen |
Ì |
null gehen. |
10.1.3 Schnittkurven mit Ebenen und Höhenlinien
Um einen Eindruck vom Verlauf einer Fläche zu bekommen, kann man Schnitte durch das Funktionsschaubild legen. In einer Schnittebene wird die Fläche auf eine Kurve reduziert. Man erhält also ein zweidimensionales Schaubild, wie wir es bereits von Funktionen mit einer Variablen kennen.
10.1 Definition und Darstellung |
389 |
Am einfachsten sind vertikale und horizontale Schnitte zu realisieren. Durch Festhalten der Größen x = x0, y = y0 oder z = z0 erhält man Schnittkurven, die parallel zur y-z-Ebene, zur x-z-Ebene oder zur x-y-Ebene verlaufen. Spezielle Schnittkurven erhält man für x0 = 0, y0 = 0 oder z0 = 0. Dann gehen die Schnittebenen durch den Ursprung.
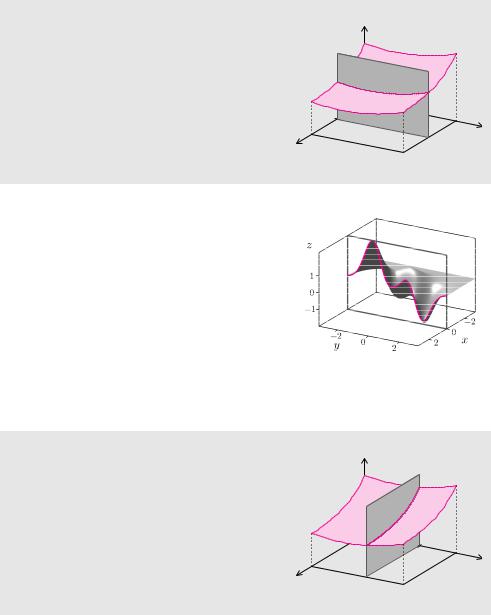
Schnitte mit Ebenen parallel zur y-z-Ebene |
|
|
|
|||||||||
Schneidet |
|
man |
das Schaubild |
einer |
Funktion |
|
|
z |
||||
mit zwei Variablen z |
f |
x, y |
mit der Ebene |
|
|
|
||||||
x x |
|
|
|
die Funktionsgleichung |
|
|
|
|||||
= |
0, so erhält man= |
( |
|
) |
|
|
|
|
|
|||
der Schnittkurve |
|
|
|
|
|
|
|
|
||||
|
z g y |
f x0, y |
|
|
|
|
|
|
|
g(y) |
||
|
|
|
|
|
|
|
|
|
||||
durch Einsetzen= ( ) = des( festen) |
Wertes x |
x0 in die |
x |
x0 |
y |
|||||||
Funktion |
f |
. Dabei liegt die |
Schnittkurve in ei- |
|
|
|
||||||
|
|
= |
|
|
|
|
||||||
ner Ebene, die parallel zur y-z-Ebene verläuft.
Beispiel 10.2 (Peaks geschnitten mit y-z-Ebene)
Die Schnittkurve der Funktion aus Beispiel 10.1 mit der y-z-Ebene erhalten wir durch Einsetzen von x = 0 in die Funktionsgleichung
g(y) = e−(1−y)2 − 3y5 e−y2 − e−1−y2 .
Dadurch ergibt sich eine Funktion g(y), die nur von der Variablen y abhängt.
Ì
Schnittkurven mit Ebenen parallel zur y-z-Ebene oder zur x-z-Ebene einer Funktion mit zwei Variablen lassen sich problemlos durch Einsetzen entsprechender Werte ermitteln. Die Schnittkurven sind Schaubilder von Funktionen in der jeweiligen Schnittebene.
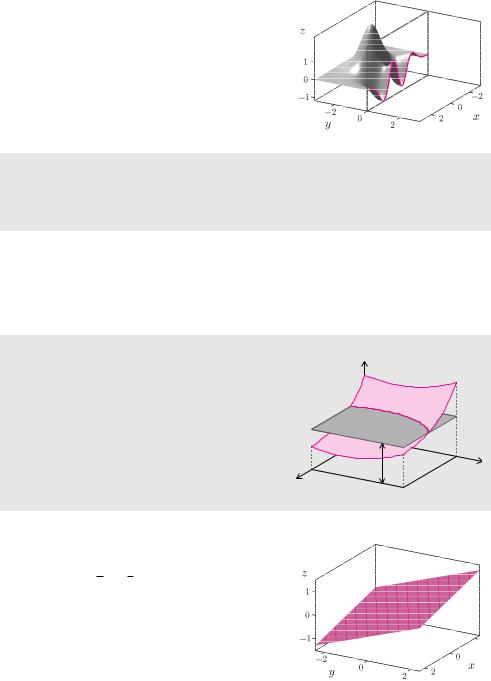
Schnitte mit Ebenen parallel zur x-z-Ebene |
|
|
||||||||||||
Schneidet |
man |
das Schaubild |
einer |
Funktion |
|
z |
||||||||
mit zwei Variablen z |
f x, y |
|
mit der Ebene |
|
|
|||||||||
y y |
0, |
so |
erhält |
man= |
die |
|
Funktionsgleichung |
|
g(x) |
|||||
= |
( |
|
|
) |
|
|
|
|||||||
der Schnittkurve |
|
|
|
|
|
|
|
|
|
|||||
|
z |
|
g x |
f |
x, y0 |
|
|
|
|
|
|
|
|
|
durch Einsetzen= ( ) = des( festen) |
Wertes y |
y0 in die |
x |
y |
||||||||||
Funktion |
f |
. Dabei liegt die |
Schnittkurve in ei- |
|
|
|||||||||
|
|
|
= |
|
|
|
||||||||
ner Ebene, die parallel zur x-z-Ebene verläuft.
390 |
10 Funktionen mit mehreren Variablen |
Beispiel 10.3 (Peaks geschnitten mit x-z-Ebene)
Die Schnittkurve der Funktion aus Beispiel 10.1 mit der x-z-Ebene erhalten wir durch Einsetzen von y = 0 in die Funktionsgleichung
g(x)=(1+x)2e−x2−1−3(x3−x)e−x2−e−(1−x)2 .
Die entstehende Funktion g(x) hängt nur von der
Variablen x ab.
Ì
Definition 10.2 (Höhenlinien)
Die Schnittkurven der Ebenen z = z0, die parallel zur x-y-Ebene verlaufen, mit dem Schaubild der Funktion z = f(x, y) nennt man Höhenlinien, Konturlinien oder Niveaulinien.
Während die Schnittkurven für x = x0 und y = y0 Kurven in expliziter Form ergeben, ist die Situation bei Schnittkurven für z = z0 anders. Hier entstehen Kurven in impliziter Darstellung. Dies erschwert in der Regel das Erstellen einer Grafik mit x-y-Schnittkurven. Anschaulich kann man sich die Niveaulinien als Höhenlinien eines Gebirges vorstellen. Bei Landkarten bezeichnet man Höhenlinien als Isohypsen.
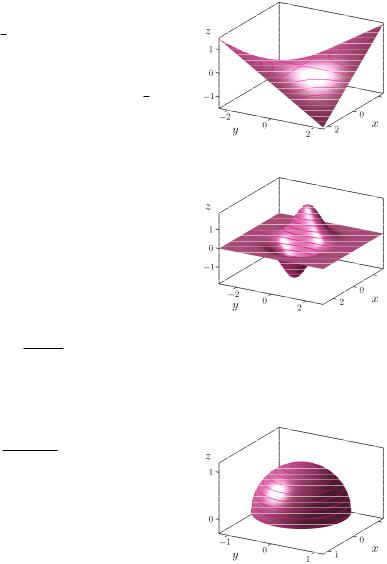
Höhenlinien |
|
|
|
|
|
||||
Die Höhenlinien der Funktion z |
f x, y |
zum |
z |
||||||
Niveau |
z |
|
z |
0 |
, erfüllen die |
implizite Gleichung |
|
||
|
= |
|
= |
( |
) |
|
|||
|
|
|
|
|
|
|
|
|
|
z0 =f(x, y)
z0 = f(x, y).
Entlang einer Höhenlinie hat die Funktion f |
|
y |
|
den konstanten Wert z0. Höhenlinien zu un- |
|
||
x |
z0 |
||
terschiedlichen Niveauwerten z0 schneiden sich |
|||
nicht. |
|
|
Beispiel 10.4 (Ebene)
Die Funktion
f(x, y) = −1 x + 1 y
53
ist eine lineare Funktion in x und y. Die Funktion ist auf ganz R2 definiert. Alle Schnittkurven mit Ebenen sind Geraden. Das Schaubild ist eine Ebene. In x-Richtung nehmen die Funktionswerte ab und in y-Richtung nehmen sie zu.
Ì
10.1 Definition und Darstellung |
391 |
Beispiel 10.5 (Hyperbolisches Paraboloid)
Das Schaubild der Funktion
f(x, y) = −1 x y
4
besteht aus einem sogenannten hyperbolischen Paraboloid. Die Schnittkurven für x = x0 und y = y0 sind
Geraden. Höhenlinien haben die Form z0 = −1 x y,
4
sie sind also rechtwinklige Hyperbeln.
Ì
Beispiel 10.6 (Zusammengesetzte Exponentialfunktion)
Die Funktion
f(x, y) = −4 x e−(x2+y2)
entsteht im Wesentlichen durch Multiplikation der Variablen x mit einer Exponentialfunktion. Je weiter man sich vom Ursprung entfernt, desto kleiner werden die Funktionswerte.
Ì
Rotationssymmetrische Funktionen sind Funktionen, bei denen der Funktionswert f(x, y)
»
nur von Radius r = x2 + y2 abhängt. Die unabhängigen Variablen treten also nur in der Form x2 + y2 auf. Die Schaubilder solcher Funktionen sind rotationssymmetrisch bezüglich der z-Achse. Die Höhenlinien von Rotationsflächen sind konzentrische Kreise.
Beispiel 10.7 (Halbkugel)
Das Schaubild der rotationssymmetrischen Funktion
»
f(x, y) = 1 − x2 − y2
stellt die obere Hälfte der Kugel mit Radius 1 und Mittelpunkt im Ursprung dar. Definitionsund Wertebereich sind
D = {(x, y) S x2 + y2 ≤ 1}, W = [0, 1].
Die Schnittkurven für x0 = 0 und y0 = 0 sind
» |
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
g1(y) = 1 − y2, g2(x) = 1 − y2, |
|
|
|
|
|
|
|
≤ |
|
≤ |
|
||||
also Halbkreise um den Ursprung mit Radius 1. Höhenlinien existieren für 0 |
z0 |
1, nämlich |
|||||||||||||
implizit in der Form |
|
|
|
|
|
|
|
|
|
|
|
|
|||
x2 + y2 = 1 − z02. |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
» |
1 |
− |
z2 |
|
|
|
Ì |
||||
Dies sind konzentrische Kreise um den Ursprung mit Radius |
|
|
0. |
|
|
|
|||||||||
