
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

155
5 Funktionen
Der Funktionsbegri bildet das Herzstück der modernen Mathematik. Er ist das Bindeglied zwischen Technik, Wirtschaftswissenschaften und Naturwissenschaft einerseits und der Mathematik andererseits. Wenn es gelingt, die Funktionsweise einer konkreten Anwendung mithilfe von mathematischen Funktionen darzustellen, dann bietet die Mathematik ein reichhaltiges Repertoire zur Analyse dieser Funktionsweise.
5.1 Einführung
Die wesentlichen Begri e zur Darstellung von Funktionen werden bereits in der Schulmathematik behandelt. Trotzdem greifen wir sie an dieser Stelle nochmals auf und illustrieren sie anhand von Beispielen.
5.1.1 Begri der Funktion
Der Begri Funktion wird in der Mathematik sehr allgemein gefasst. Typischerweise definiert man eine Funktion als eine Abbildung von einer Menge in eine andere Menge. Für unsere Zwecke reicht es jedoch aus, diese abstrakte Sichtweise für den Fall einer Abbildung zwischen reellen Zahlen zu konkretisieren.
Definition 5.1 (Reelle Funktion)
Unter einer reellen Funktion f versteht man eine Abbildung, die jeder reellen Zahl x aus einer Definitionsmenge D R genau eine reelle Zahl y aus einer Wertemenge W zuordnet.
x ( y = f(x), x D.
Man bezeichnet x als unabhängige Variable und y als abhängige Variable.
Üblich ist auch die Schreibweise f D → W oder allgemeiner f R → R. Streng genommen sollte man in der Mathematik genau zwischen f und f(x) unterscheiden. f ist der Name der Funktion und f(x) der Wert, der x zugeordnet ist. In der Definition ist x ein Platzhalter; man könnte auch andere Bezeichnungen wie etwa f(u) oder f(t) wählen. Manchmal sagt man auch Definitionsund Wertebereich anstelle von Definitionsund Wertemenge.

156
b)Die Funktion f(x) = −x2 + 2 x + 8 ist für alle x-Werte definiert, für die der Ausdruck unter der Wurzel nicht negativ wird. Diese x-Werte erfüllen die Bedingung −x2 + 2 x + 8 ≥ 0. Die Lösungen der Gleichung −x2 + 2 x + 8 = 0 ergeben sich zu
√
x1,2 = −2 ± 4 + 32 = −2, 4.
−2
Für x-Werte zwischen 2 und 4 ist der Ausdruck unter der Wurzel nicht negativ, also ist der
maximale |
Definitionsbereich D |
|
2, 4 . |
|
− |
= [− |
] |
Ì |
|
|
|
Wertebereich
Zur Bestimmung des Wertebereichs einer Funktion benötigt man in der Regel einige Informationen über die Funktion, wie etwa die Extremwerte, die Monotonieeigenschaften und das asymptotische Verhalten.
Wie man solche Informationen für Funktionen systematisch erhält, werden wir später genauer betrachten. Bei einfachen Funktionen lässt sich der Wertebereich durch einfache Überlegungen ermitteln. Manchmal spricht man bei f(D) auch vom sogenannten Bildbereich der Funktion f.
Beispiel 5.2 (Wertebereich) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a) Welchen Wertebereich |
hat |
die |
Funktion |
f x |
|
|
|
|
|
? |
Dazu überlegen wir |
uns, welche |
|||||||||||||||||||||||||||||
|
1 |
|
x |
||||||||||||||||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
durchlaufen. |
|||||
|
-Werte sich ergeben, wenn die |
-Werte |
den Definitionsbereich D |
|
R |
||||||||||||||||||||||||||||||||||||
|
|
|
|
( |
|
) = |
|
− |
|
|
|
|
|
|
= |
{ } |
|
||||||||||||||||||||||||
|
Durch Auflösen der Gleichung nach x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y = |
|
|
|
Ô |
x = 1 |
− |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 x |
y |
|
|
|
|
|
y |
|
|
0 einen passenden |
x |
-Wert gibt. Der Werte- |
|||||||||||||||||||||||||||
|
erkennen−wir, dass es zu jeder reellen Zahl |
|
|
≠ |
|
||||||||||||||||||||||||||||||||||||
|
bereich ist somit W |
R |
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
b) |
Zur Bestimmung |
des Wertebereichs der Funktion f x |
|
|
|
|
|
|
|
formen wir den |
|||||||||||||||||||||||||||||||
|
|
x2 |
|
2 x |
|
8 |
|||||||||||||||||||||||||||||||||||
|
|
= |
{ } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) = − |
|
+ |
|
|
+ |
|
|
|
||||||||||||||
|
Ausdruck unter der Wurzel durch quadratisches Ergänzen |
um |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
√ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
» |
|
|
|
|
|
|
|
|
|
|
|
» |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
f x |
|
x2 |
− |
2 x |
+ |
1 |
) + |
9 |
|
= |
−( |
x |
1 |
) |
2 |
+ |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Der ( |
) = −( |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Ausdruck unter der Wurzel hat für x 1 den maximalen Wert 9. Der Wertebereich der |
|||||||||||||||||||||||||||||||||||||||
|
Funktion besteht aus dem Intervall |
W |
|
0, 3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
= [ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

5.1 Einführung |
157 |
In der Mathematik sind im Zusammenhang mit dem Definitionsund Wertebereich einer Funktion noch die Begri e Injektivität, Surjektivität und Bijektivität gebräuchlich.
Definition 5.2 (Injektive, surjektive und bijektive Funktion)
Eine Funktion f D → W heißt
Linjektiv, falls jeder Funktionswert y ein eindeutiges Argument x mit f(x) = y hat,
Lsurjektiv, falls jede Zahl y aus der Wertemenge W auch tatsächlich mindestens einmal als Funktionswert angenommen wird,
Lbijektiv, falls f sowohl injektiv als auch surjektiv ist.
Bei bijektiven Funktionen spricht man auch von sogenannten ein-ein-deutigen Funktionen. Sie sind also sowohl von x nach y als auch in der Rückrichtung von y nach x eindeutig. Sie werden im Zusammenhang mit Umkehrfunktionen in Abschnitt 5.7 noch eine wesentliche Rolle spielen.
Beispiel 5.3 (Injektive, surjektive und bijektive Funktionen)
a)Die Funktion f R → R mit f(x) = x3 ist injektiv und surjektiv und damit auch bijektiv. Jeder Wert y aus R wird von der Funktion f angenommen, und zwar genau einmal.
b)Die Funktion f R → R mit f(x) = x2 ist nicht injektiv und nicht surjektiv. Alle negativen Zahlen werden durch f, also durch Quadrieren, nicht erzeugt. Alle positiven Zahlen hingegen werden doppelt erzeugt, denn es ist
f(x) = f(−x) = x2.
c)Die Funktion f R → [0, ∞) mit f(x) = x2 ist nicht injektiv, aber surjektiv. Hier wird jeder Wert des Intervalls [0, ∞) von der Funktion f erzeugt, abgesehen von der null jeweils sogar doppelt.
d)Die Funktion f [0, ∞) → R mit f(x) = x2 ist injektiv, aber nicht surjektiv. Negative Werte nimmt f nicht an.
e) Die Funktion f [0, ∞) → [0, ∞) mit f(x) = x2 ist bijektiv. |
Ì |
Definition 5.3 (Nullstelle)
Eine Nullstelle einer Funktion f ist ein x-Wert, an dem die Funktion den Wert null hat. Eine Nullstelle erfüllt die Gleichung f(x) = 0.
Bei einfachen Funktionen f, wie beispielsweise bei Geraden und Parabeln, kann man alle Nullstellen durch Lösen der Gleichung f(x) = 0 bestimmen. Je nach Typ der Funktion kann die Bestimmung der Nullstellen aufwendig sein. Oft ist man zur Berechnung von Nullstellen auf numerische Näherungsverfahren angewiesen. In manchen Fällen ist es sogar problematisch, verlässliche Aussagen über die Anzahl der Nullstellen einer Funktion zu tre en.

158 |
5 Funktionen |
5.1.2 Wertetabelle
Kennt man für die Funktion eine explizite Funktionsgleichung, dann kann man die Zuordnung der y-Werte zu den x-Werten in Form einer Tabelle wiedergeben. Dazu berechnet man die Funktionswerte für ausgewählte x-Werte.
Wertetabelle
Eine Wertetabelle einer Funktion enthält die Zuordnung der Funktionswerte zu einigen speziellen x-Werten. Damit die Tabelle das Verhalten der Funktion gut beschreibt, müssen die x-Werte geeignet ausgewählt werden.
Beispiel 5.4 (Wertetabelle einer Funktion)
2
Wir erstellen für die Funktion f(x) = eine Wertetabelle für x-Werte im Bereich von −5 bis
1 − x
5. Dazu verwenden wir, wie in der Schule üblich, x-Werte im Abstand von 1.
x |
5 |
4 |
3 |
2 |
|
1 |
0 |
1 |
2 |
3 |
|
4 |
|
5 |
|
||||||||||
y |
−1 |
−2 |
−1 |
−2 |
− |
1 |
2 |
− |
−2 |
−1 |
− |
2 |
− |
1 |
|
||||||||||
|
3 |
|
|
5 |
|
|
2 |
|
|
3 |
|
|
3 |
|
2 |
|
Ì |
||||||||
Wertetabellen lassen sich mithilfe von Computern einfach erstellen. Oftmals übersieht man, dass der Informationsgehalt einer Wertetabelle weitaus geringer ist als der Informationsgehalt einer Funktionsgleichung. Durch eine Funktionsgleichung sind unendlich viele Funktionswerte definiert, eine Wertetabelle erfasst lediglich eine endliche Anzahl von Werten. In diesem Zusammenhang spricht man auch von einer Diskretisierung der Funktion.
5.1.3 Schaubild
In der Regel fällt es sehr schwer, Informationen aus Zahlenkolonnen zu erfassen. Andererseits verfügt das menschliche Gehirn über hervorragende Fähigkeiten, Bilder entsprechend zu interpretieren. Deshalb verwendet man gerne eine visuelle Darstellung einer Funktion mithilfe von Schaubildern.
Definition 5.4 (Schaubild, Graph)
Die grafische Darstellung der Punkte (x S f(x)) in einem kartesischen Koordinatensystem nennt man Schaubild oder Graph der Funktion f.
Schaubilder von Funktionen lassen sich ebenfalls mithilfe von Computern mühelos erstellen. Doch genau wie bei einer Wertetabelle ist der Computer lediglich in der Lage, endlich viele Werte herauszugreifen und damit ein Schaubild zu erstellen. Auch wenn die Computerprogramme zur Visualisierung von Funktionen in den vergangenen Jahren einen beachtlichen Stand erreicht haben, gehört es zu den Kompetenzen eines Ingenieurs, den Verlauf einfacher Funktionen, zumindest in Gedanken, skizzieren zu können.
5.1 Einführung |
159 |
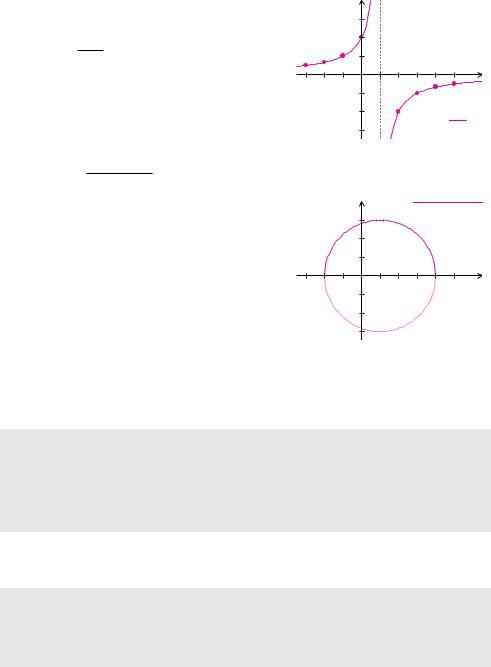
Beispiel 5.5 (Schaubilder von Funktionen)
a) |
Mithilfe der Wertetabelle aus Beispiel 5.4 kann |
|
|
y |
|
|
|
|
|
|||||
|
man den ungefähren Verlauf der Funktion |
|
|
3 |
|
|
|
|
|
|||||
|
f(x) = |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
|
|
|
|
1 |
|
|
|
|
|
||
|
skizzieren. |
An der Stelle x 1 ist kein Funktions- |
3 |
2 |
1 |
1 |
2 |
3 |
4 |
x |
||||
|
|
− |
|
|
|
|||||||||
|
wert definiert. Das |
Verhalten in der Nähe dieser |
− |
− |
− |
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
− |
|
|
|
|
|
||||||
|
|
= |
|
|
|
|
|
|
|
|||||
|
Definitionslücke werden wir später noch genauer |
|
|
−2 |
|
|
|
|
2x |
|||||
|
betrachten. |
|
|
|
|
|
|
|
|
f (x) = 1 |
||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
b) In Beispiel 5.1 haben wir bereits gesehen, dass die Funktion |
|
|
|
|
|
|
||||||||
|
f(x) = √−x2 + 2 x + 8 |
|
|
|
|
|
|
|
|
|
||||
nur für x-Werte im Intervall von −2 bis 4 definiert ist. Tatsächlich besteht das Schaubild aus dem oberen Halbkreis mit Mittelpunkt (1 S 0) und Radius 3, denn es gilt
f(x)2 = −(x − 1)2 + 9,
was der Kreisgleichung
(x − 1)2 + y2 = 9
entspricht.
y |
f (x) = −x2 + 2x + 8 |
|
3 |
||
2 |
|
|
1 |
|
|
−3 −2 −1 |
1 2 3 4 5 |
x |
−1 |
|
|
−2 |
|
|
−3 |
|
|
Ì
Eine Funktion kann keine, genau eine oder auch mehrere Nullstellen, also Schnittpunkte mit der x-Achse, haben.
Schnitte mit x-Achse
Die x-Werte der Schnittpunkte des Schaubilds der Funktion f mit der x-Achse, also die Nullstellen, bestimmt man aus der Gleichung
f(x) = 0.
Eine Funktion hat genau einen Schnittpunkt mit der y-Achse, falls x = 0 im Definitionsbereich der Funktion liegt. Ansonsten kommt natürlich kein Schnitt zustande.
Schnitt mit y-Achse
Den y-Wert des Schnittpunktes des Schaubildes der Funktion f mit der y-Achse kann man durch Einsetzen von x = 0 in die Funktionsgleichung berechnen, falls x = 0 im Definitionsbereich von f liegt.
