
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
336 |
7 Integralrechnung |
7.5.2 Romberg-Verfahren
Mit dem Romberg-Verfahren kann man aus Näherungswerten, die man mit der Trapezregel berechnet hat, einen noch besseren Näherungswert erzeugen. Die Idee besteht dabei darin, die Näherungswerte der Trapezregel als Funktion der Schrittweite h zu interpretieren. Aus theoretischer Sicht würde die Trapezregel mit Schrittweite h = 0 ein exaktes Ergebnis liefern. Praktisch kann man die Schrittweite h = 0 natürlich nicht verwenden. Man versucht deshalb, den Wert der Trapezregel mit Schrittweite h = 0 durch Extrapolation bekannter Werte möglichst gut zu schätzen. Eine genaue Beschreibung findet man bei [Mohr:Numerik].
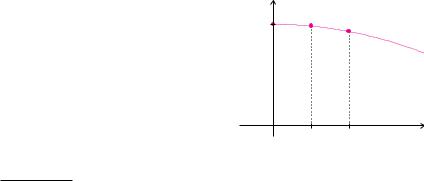
Beispiel 7.36 (Romberg-Verfahren)
Wir verwenden die Näherungswerte aus Beispiel 7.35
T (4) ≈ 4.9698, T (2) ≈ 5.2575
und bestimmen eine Parabel T (h) = a h2 + c, die durch diese Punkte verläuft. Aus den beiden Gleichungen
T (4) = 16 a + c, T (2) = 4 a + c
lässt sich c ermitteln:
T (h) |
T (2) |
|
|
c |
T (4) |
|
|
|
|
||
|
2 |
4 |
h |
c = |
4 T (2)3− T (4) |
≈ 5.3534. |
= |
|
Dieser Wert ist der Funktionswert der Parabel an der Stelle h |
0 und somit eine gute Schätzung |
|||
für den gesuchten Wert. |
Ì |
|||
7.6 Anwendungen
Wenn es bei Anwendungen darum geht, Funktionswerte über einen bestimmten Bereich zu summieren, kommen oft Integrale zum Einsatz. Wir betrachten zwei typische Beispiele, eines aus der Elektrotechnik und eines aus der Mechanik. Beim E ektivwert in der Elektrotechnik wird der zeitliche Verlauf eines Signals integriert. Bei Schwerpunkten und statischen Momenten in der Mechanik werden Funktionen über eine räumliche Distanz integriert.
7.6.1 E ektivwert
Energie, die wir über die Steckdose aus dem Stromnetz beziehen, ist in der Regel kein Gleichstrom, sondern Wechselstrom. In den meistern Ländern erfolgt die Spannungsversorgung durch sinusförmige Wechselspannungen mit einer Frequenz von 50 Hz oder 60 Hz. In Deutschland findet man auf Steckdosen und Geräten oft die Bezeichnung 230 V. Diese

7.6 Anwendungen |
337 |
Angabe bezeichnet aber nicht, wie oft behauptet wird, die Amplitude der sinusförmigen Wechselspannung. Tatsächlich liegt die Amplitude bei etwa 325 V. In der Elektrotechnik bezeichnet man diesen Wert als Scheitelwert. Den Zusammenhang zwischen diesen beiden Angaben, also 230 V einerseits und Scheitelwert 325 V andererseits, werden wir im Folgenden klären.
Für den Verbraucher ist letztendlich entscheidend, welche Energie bzw. Leistung zur Verfügung gestellt wird. Zu diesem Zweck betrachtet man den sogenannten E ektivwert. Der E ektivwert ist folgendermaßen definiert: Bei einer Wechselspannung wird an einem ohmschen Widerstand über einen gewissen Zeitraum dieselbe Leistung umgesetzt wie bei einer Gleichspannung, deren Spannung dem E ektivwert entspricht. Aus der Elektrotechnik kennt man die Formel zur Berechnung des E ektivwerts, siehe [Küpfmüller],
|
|
¾ |
|
|
|
|
|
|
|
|
Ue |
= |
|
1 |
|
T u2 |
t |
) |
dt. |
||
|
T S0 |
|||||||||
|
|
|
|
( |
|
|
||||
Dabei bezeichnet T die Periodendauer. Bei einer sinusförmigen Wechselspannung mit
Kreisfrequenz ω |
= |
2 π |
|
|
|
|
|
|
ˆ |
||||
|
T |
und Scheitelwert U erhalten wir |
|||||||||||
|
|
¾ |
|
|
|
|
|
|
|
|
|
|
|
Ue |
= |
1 |
|
S0 |
T Uˆ2 sin2 |
( |
ω t |
dt. |
|||||
|
|
|
|||||||||||
|
|
|
T |
|
|
t |
|
) |
|
|
|||
Mit der Substitution x = ω2 π ergibt sich |
|||||||||||||
|
|
Uˆ ¾ |
|
|
|
|
|
||||||
Ue |
= |
1 |
S |
sin2 x dx. |
|||||||||
|
2 π |
||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Der E ektivwert ist also unabhängig von der Periode T und der Kreisfrequenz ω. Das Integral berechnen wir mithilfe einer Stammfunktion, siehe Beispiel 7.22,
|
|
|
|
¿ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
2 π |
|
|
|
|
|
|
Uˆ |
1 |
. |
|||
U |
e |
|
Uˆ |
|
sin x cos x |
x |
|
Uˆ |
|
1 |
π |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
0 |
|
|
|
|
|
||||||||||||
|
|
= |
|
ÀÁ |
|
|
‹− |
( |
|
− |
)•V |
= |
|
|
|
|
= |
√ |
||||
Bei einem sinusförmigen Verlauf ist der Scheitelwert also immer um den Faktor |
2 größer |
||||||||
als der E ektivwert. Bei einem Scheitelwert von |
ˆ |
|
325 |
|
ektivwert |
||||
U |
|
|
|||||||
|
= |
|
V erhaten wir den E √ |
||||||
1 |
|
|
|
|
|
|
|||
Ue = |
√ |
|
|
325 V ≈ 230 V. |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
7.6.2 Schwerpunkte und statische Momente ebener Flächen
Der Schwerpunkt eines Objekts ist in der technischen Mechanik von zentraler Bedeutung. Kräfte, die im Schwerpunkt angreifen, verändern das Rotationsverhalten nicht. Oder anders formuliert, wirkt eine Kraft in einer gewissen Entfernung vom Schwerpunkt auf ein
338 |
7 Integralrechnung |
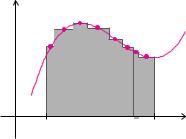
Objekt, so entsteht ein Drehmoment, siehe Abschnitt 3.5.3. Unser Ziel ist, den Schwerpunkt einer ebenen Fläche, die durch das Schaubild einer nicht negativen, stetigen Funktion f für x-Werte zwischen a und b mit der x-Achse begrenzt wird, zu bestimmen. Ein Schwerpunkt ist ein Gleichgewichtspunkt von Drehmomenten. Wir müssen also zuerst klären, welche Drehmomente auf unsere Flächen wirken. Dazu betrachten wir einen Körper mit sehr kleiner konstanter Dicke ε > 0, dessen Grundfläche gerade unsere Fläche ist. Den Körper könnten wir auf einer Bleistiftspitze balancieren, sofern wir die Spitze genau im Schwerpunkt ansetzen.
Wir zerlegen den Körper in n Körper mit rechteckiger Grundfläche. Alle Rechtecke haben eine Grundseite der Länge x. Die Höhe der Rechtecke f(xk) hängt vom Verlauf der Funktion f ab. Das Volumen Vk eines rechteckigen Körpers ergibt sich aus dem Flächeninhalt Ak des Rechtecks und der Dicke ε. Bei einem homogenen Körper, also bei einem Körper, der überall die konstante Dichte % hat, besitzen diese rechteckigen Körper die Masse
mk = % Vk = % Ak ε = % x f(xk) ε.
y |
f(xk) |
|
|
|
|
a |
b |
x |
|
xk |
|
|
|{z} |
|
Mit der Erdbeschleunigung g wirkt auf diese Masse die Gewichtskraft F k vom Betrag
Fk = SF kS = mk g = % x f(xk) ε g.
Der Schwerpunkt einer Rechteckfläche hat die Koordinaten Sk(xk S 12 f(xk)). Wenn die Gewichtskraft F k senkrecht zur x-y-Ebene wirkt und wir die x-Achse als Drehachse betrachten, dann ergibt sich ein Drehmoment Mx,k mit
Mx,k |
Mx,k |
|
|
Fk 21 f xk |
|
|
21 g % ε f xk 2 x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Dabei hängt=dasS |
Drehmoment von der Länge des Hebels, also vom Abstand |
1 f x |
k |
|||||||||||||||||||||||||||
|
S = |
|
x |
|
( |
|
) = |
|
|
|
( |
) |
|
|
|
M |
|
|
|
|
|
|
2 |
|
||||||
des Schwerpunktes von der |
-Achse ab. Das Gesamtdrehmoment |
x erhalten wir |
durch |
|||||||||||||||||||||||||||
|
|
( |
) |
|||||||||||||||||||||||||||
Grenzübergang der Summe aller Einzeldrehmomente |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
n |
|
|
= |
|
|
|
|
n |
|
( |
|
) |
|
|
n→∞ |
|
= |
|
|
|
|
b |
( |
|
) |
|
|
|
Mx |
|
Mx,k |
21 g % ε |
kQ1 |
f |
xk |
2 x |
|
Mx |
21 g % ε |
a |
f2 |
x |
dx. |
|
|||||||||||||||
|
≈ kQ1 |
|
|
|
|
|
|
|
|
|
ÐÐÐ→ |
|
|
|
|
S |
|
|
|
|
|
|||||||||
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bezüglich der y-Achse erhalten wir das Drehmoment My,k mit |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
My,k = SMy,kS = Fk xk = g % ε xk f(xk) |
x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Hier geht der Abstand zur y-Achse xk ein. Bezogen auf die y-Achse erhalten wir das Gesamtdrehmoment
|
n |
|
|
n |
|
|
|
|
n→∞ |
|
|
|
|
b |
|
My |
≈ kQ1 |
My,k |
= |
g % ε |
xk f |
xk |
) |
x |
My |
= |
g % ε |
a |
x f x |
dx. |
|
|
|
kQ1 |
( |
|
|
ÐÐÐ→ |
|
|
S |
( ) |
|
||||
|
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
Ohne Berücksichtigung der physikalischen Größen g, % und ε bezeichnet man diese Drehmomente als statische Momente einer ebenen Fläche.

7.6 Anwendungen |
339 |
Definition 7.7 (Statische Momente)
Das Flächenstück, das durch das Schaubild einer nicht negativen, stetigen Funktion f für x-Werte zwischen a und b und der x-Achse begrenzt wird, besitzt das
L |
statische Moment bezüglich der x-Achse |
Mx = 21 |
|
ba |
b |
|
f2(x) dx, |
||||
L |
|
|
S |
|
|
statische Moment bezüglich der y-Achse |
My = Sa |
x f(x) dx. |
|||
Die Koordinaten des Schwerpunkts S(xS S yS) der Fläche ergeben sich durch den Vergleich der Momente. Dazu stellen wir uns vor, dass die gesamte Masse m des Körpers im Schwerpunkt konzentriert ist. Die Gewichtskraft des gesamten Körpers beträgt dann
F = SF S = m g = % A ε g,
wobei A der Flächeninhalt der Fläche ist. Für die Gesamtdrehmomente gilt dann
|
Mx |
= |
F yS |
= |
% A ε g yS |
, My |
= |
F xS |
= |
% A ε g xS. |
|
|
||||||
Der |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Vergleich der Drehmomente ergibt |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
1 |
|
|
b |
||
|
% A ε g yS = 21 g % ε Sa |
|
f2(x)dx |
Ô yS = |
Sa |
f2(x)dx |
||||||||||||
|
|
|
|
|
||||||||||||||
und |
|
2 A |
||||||||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
1 |
|
|
b |
|
|
|
% A ε g xS = g % ε Sa |
x f(x)dx |
|
Ô xS = |
Sa |
x f(x)dx. |
||||||||||||
|
|
|
||||||||||||||||
|
|
A |
||||||||||||||||
Wie erwartet hängen die Schwerpunktskoordinaten nicht von den physikalischen Größen g, % und ε ab.
Satz 7.20 (Schwerpunkt einer ebenen Fläche)
Die Koordinaten des Schwerpunkts S(xS S yS), des Flächenstücks, das durch das Schaubild einer nicht negativen, stetigen Funktion f für x-Werte zwischen a und b und der x-Achse begrenzt wird, kann man durch
|
My |
|
1 |
|
b |
|
Mx |
|
1 |
|
b |
||
xS = |
= |
Sa |
x f(x) dx, |
yS = |
= |
Sa |
f2(x) dx |
||||||
A |
A |
A |
|
2 A |
|||||||||
berechnen. Dabei sind Mx und My die statischen Momente bezüglich der x-Achse bzw. y-Achse und A der Flächeninhalt des Flächenstücks.
Bei den Formeln in Satz 7.20 könnte man denken, es liegt ein Tippfehler vor. Wenn man die Herleitung der Formel jedoch aufmerksam verfolgt hat, dann ist völlig klar, dass die x-Koordinate des Schwerpunkts tatsächlich in Bezug zum Moment bezüglich der y-Achse steht und die y-Koordinate tatsächlich in Bezug zum Moment bezüglich der x-Achse.
340 |
7 Integralrechnung |
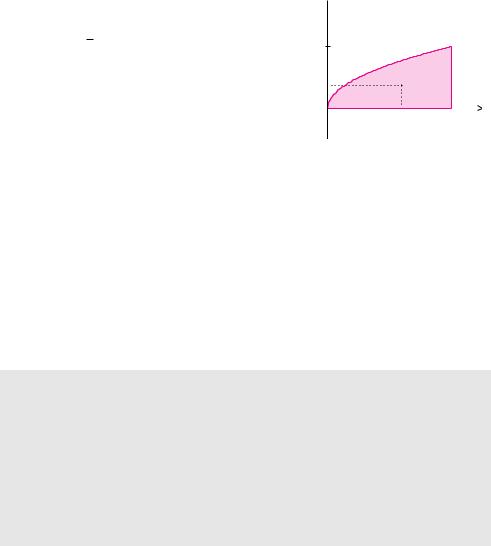
Beispiel 7.37 (Schwerpunkt einer ebenen Fläche)
Wir berechnen den Schwerpunkt der Fläche, die durch das Schaubild der Funktion
√
f(x) = x
für x-Werte zwischen 0 und 4 und der x-Achse gebildet wird. Der Flächeninhalt beträgt
A = S0 |
√x dx = 3 x2 V0 = |
3 |
|||
4 |
|
2 |
3 |
4 |
16 |
und die Koordinaten des Schwerpunktes ergeben sich zu
y 
2
yS 
 S
S
x |
|
S |
4 |
x |
||
|
3 |
|
4 |
|
|
|
3 |
2 |
5 |
4 |
12 |
|
3 |
|
4 |
|
3 |
4 |
3 |
|
|
||||
xS = |
|
S0 |
|
x √x dx = |
|
|
|
x 2 V0 = |
|
|
, yS = |
|
S0 |
|
x dx = |
|
|
x2V0 = |
|
|
. |
Ì |
|||
16 |
|
16 |
5 |
5 |
32 |
|
64 |
4 |
|||||||||||||||||
Die Formel für das Rotationsvolumen aus Satz 7.17 und die Formel für die y-Koordinate des Schwerpunkts aus Satz 7.20 enthalten beide das Integral über das Quadrat der Funktion. Dadurch ergibt sich ein Zusammenhang zwischen Rotationsvolumen, Schwerpunktkoordinaten und Flächeninhalt:
|
|
b |
1 |
|
b |
Vx |
|
|
Vx = π |
a |
f(x)2 dx, yS = |
a |
f2(x) dx Ô |
= 2 A yS. |
|||
2 A |
π |
|||||||
|
S |
|
|
S |
|
|
|
Ein ähnlicher Zusammenhang gilt auch für die x-Koordinate des Schwerpunkts.
Satz 7.21 (2. Guldinsche Regel)
Das Flächenstück, das durch das Schaubild einer nicht negativen, stetigen Funktion f für x-Werte zwischen a und b und der x-Achse begrenzt wird, besitzt den Flächeninhalt A und den Schwerpunkt mit den Koordinaten S(xS S yS).
LFür das Volumen Vx, das durch Rotation des Flächenstücks um die x-Achse entsteht, gilt Vx = 2 π yS A.
LFür das Volumen Vy, das durch Rotation des Flächenstücks um die y-Achse entsteht, gilt Vy = 2 π xS A.
Die 2. Guldinsche Regel lässt sich noch allgemeiner formulieren. Zwischen Flächeninhalt A, Rotationsvolumen V und Abstand r des Flächenschwerpunktes von der Rotationsachse gilt V = 2 π r A.
Die 1. Guldinsche Regel stellt einen Zusammenhang zwischen Mantelfläche und Bogenlänge her. Weitere Einzelheiten dazu findet man bei [Bartsch].
