
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
436 |
11 Komplexe Zahlen und Funktionen |
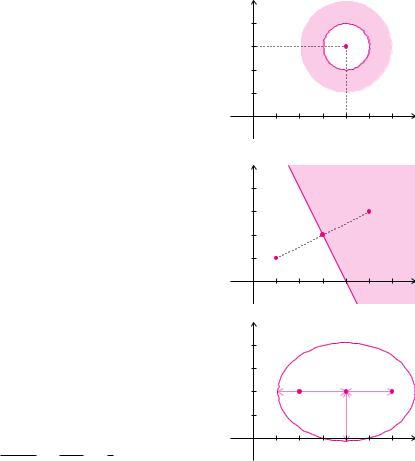
Beispiel 11.6 (Beträge komplexer Zahlen)
a) Gesucht sind alle komplexen Zahlen z mit
1 ≤ Sz − 4 − 3 iS < 2.
Aus der Darstellung
1 ≤ Sz − (4 + 3 i)S < 2
erkennen wir, dass es sich um alle komplexen Zahlen z handelt, die von z0 = 4 + 3 i einen Abstand größer gleich 1 und echt kleiner 2 haben.
b) Bei der Menge aller Zahlen z mit
Sz − (1 + i)S ≥ Sz − (5 + 3 i)S
ist der Abstand der Zahlen z zur festen Zahl z1 = 1 + i größer oder gleich dem Abstand zur Zahl z2 = 5 + 3 i. Alle Zahlen z auf der Mittelsenkrechten durch z0 = 12 (z1 + z2) = 3 + 2 i haben denselben Abstand zu z1 und z2. Somit liegen die Zahlen z alle in einer Halbebene.
c) Bei allen Zahlen z mit der Eigenschaft |
|
|||||||||||
|
z |
|
2 2 i |
|
z |
|
6 2 i |
6 |
|
|
||
hatS die− (Summe+ )Sder+ S |
Abstände− ( + )Szu= z1 |
2 2 i und |
||||||||||
z1 6 |
|
2 i |
den6Wert |
6 |
. Es ist eine= |
Ellipse mit |
||||||
= |
+ |
|
|
|
+ |
|||||||
|
|
2 |
, siehe Definition 9.5. Die Ex- |
|||||||||
Halbachse a |
|
|||||||||||
zentrizität e = |
2 entspricht dem halben Abstand |
|||||||||||
der |
Brennpunkte. Daraus kann man durch |
|||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
√ √ √
b = a2 − e2 = 9 − 4 = 5
Im |
|
|
|
|
|
|
4i |
|
|
|
|
|
|
3i |
|
|
z0 |
|
|
|
|
|
|
|
|
|
|
2i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
Re |
Im |
|
|
|
|
|
|
4i |
|
|
|
|
|
|
3i |
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
2i |
|
z0 |
|
|
|
|
|
|
|
|
|
|
|
z1 |
|
|
|
|
|
|
i |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
Re |
Im |
|
|
|
|
|
|
4i |
|
|
|
|
|
|
3i |
|
|
|
|
|
|
2i |
z1 |
a |
z0 |
e |
z2 |
|
|
|
|
|
|
|
|
i |
|
|
b |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
Re |
die Länge der zweiten Halbachse bestimmen. |
Ì |
11.3 Potenzen, Wurzeln und Polynome
Motiviert wurde die Einführung der komplexen Zahlen durch die Gleichung z2 = −1. Wir verallgemeinern diese Fragestellung auf die Bestimmung aller komplexen Nullstellen eines Polynoms. Dazu benötigen wir Potenzen und Wurzeln komplexer Zahlen.

11.3 Potenzen, Wurzeln und Polynome |
437 |
11.3.1 Potenzen
Für natürliche Hochzahlen n ist die n-te Potenz einer komplexen Zahl z genau wie bei reellen Zahlen durch
zn = z z z . . . z
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ n Faktoren
definiert, siehe Definition 1.22. Negative Potenzen entsprechen dem Kehrwert
z−n = 1 . zn
Zur Berechnung von Potenzen eignet sich die Darstellung in Exponentialform.
Satz 11.11 (Potenzen mit ganzzahligen Hochzahlen)
Für jede beliebige ganze Zahl n kann man die n-te Potenz einer komplexen Zahl in Exponentialform z = r ei ϕ durch Potenzieren der Beträge und Vervielfachen des Argumentes berechnen:
zn = ‰r ei ϕŽn = rn ei n ϕ.
Beispiel 11.7 (Potenz einer komplexen Zahl)
Die 8-te Potenz der komplexen Zahl z = 1 + i bestimmen wir nicht in kartesischer Form, sondern in Exponentialform:
z8 = (1 + i)8 = Š√2 ei π4 •8 = 24 ei 2 π = 16.
Man kann dieses Ergebnis auch mit vertretbarem Aufwand in kartesischer Form berechnen, indem man zuerst z2, dann z4 = z2 z2 und schließlich z8 = z4 z4 berechnet. Ì
11.3.2 Wurzeln
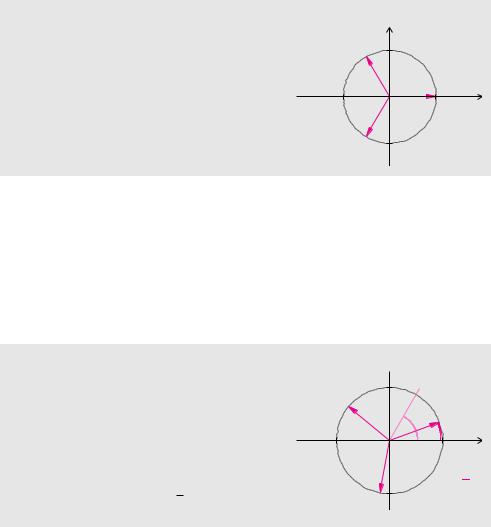
Bei Wurzeln komplexer Zahlen stellt man sich dieselbe Frage wie bei Wurzeln reeller Zahlen. Für welche komplexen Zahlen z ergibt zn den Wert a? Mit anderen Worten: Wir suchen alle Lösungen z der Gleichung zn = a, wobei a eine beliebige komplexe Zahl ist.
Definition 11.8 (Wurzeln und Einheitswurzeln)
Alle komplexen Zahlen z, die die Gleichung zn = a erfüllen, bezeichnet man als n-te Wurzeln der komplexen Zahl a. Die Lösungen der Gleichung zn = 1 nennt man die n-ten Einheitswurzeln.
Zur Bestimmung der Einheitswurzeln stellen wir z in Exponentialform dar:
z = r ei ϕ Ô zn = ‰r ei ϕŽn = rn ei n ϕ.
438 |
11 Komplexe Zahlen und Funktionen |
Aus der Gleichung zn = 1 ergibt sich damit: |
|
2 k π |
||
rn ei n ϕ = 1 Ô rn = 1, n ϕ = 0 + 2 k π |
Ô r = 1, ϕ = |
|||
|
. |
|||
n |
||||
Beim Vergleich der beiden Zahlen müssen die Radien übereinstimmen. Bei den Winkeln haben wir jedoch die Freiheit, ganzzahlige Vielfache von 2 π zu addieren. Für k erhält man dieselbe komplexe Zahl wie für k + n. Dadurch ergeben sich genau n verschiedene Einheitswurzeln.
Satz 11.12 (Komplexe Einheitswurzeln)
Es gibt genau n komplexe Zahlen
i 2 k π
ωk = e n , k = 0, 1, 2, . . . , n − 1,
die die Gleichung zn = 1 erfüllen. Die n-ten Einheitswurzeln ωk liegen, beginnend bei ω0 = 1, gleichmäßig verteilt auf dem Einheitskreis in der komplexen Zahlenebene.
n = 3 |
|
Im |
|
ω1 |
i |
|
|
−1 |
|
ω0 |
|
|
1 |
Re |
|
|
ω2 −i |
|
|
Zur Lösung der Gleichung zn = a gehen wir wie bei der Bestimmung der Einheitswurzeln vor. Wir stellen z und a in Exponentialform dar:
z = r ei ϕ, a = % ei α Ô rn ei n ϕ = % ei α.
Der Vergleich von Radien und Winkeln ergibt
|
|
|
|
|
|
α |
2 k π |
|
r |
n |
= %, n ϕ = α + 2 k π |
Ô r = |
√ |
%, ϕ = |
+n . |
||
|
|
|
n |
|
|
|||
Satz 11.13 (Komplexe Wurzeln)
Es gibt genau n komplexe Zahlen
|
= |
√ |
|
|
+n |
|
= |
|
− |
|
|
zk |
% ei |
, k |
0, 1, 2, . . . , n |
1, |
|||||||
|
n |
|
|
||||||||
|
|
|
|
|
α 2 k π |
|
|
|
|
|
|
die die Gleichung zn = a erfüllen. Dabei ist a eine beliebige komplexe Zahl mit Betrag % und Winkel α. Die n-ten Wurzeln liegen, begin-
nend bei z0, gleichmäßig verteilt auf einem Ur-
√
sprungskreis mit Radius r = n % in der komplexen Zahlenebene.
Im n = 3
n = 3
z1
%
z2
 a = % eiα
a = % eiα
|
z |
α |
0 |
α |
|
|
3 |
Re
r = |
√ |
% |
|
3 |
|
Man spricht von der Wurzel einer reellen Zahl. Im Komplexen muss man von den Wurzeln einer komplexen Zahl sprechen. Dabei versteht man unter den n-ten Wurzeln einer komplexen Zahl immer n Zahlen.
11.3 Potenzen, Wurzeln und Polynome |
439 |
Wir haben schon am Anfang dieses Kapitels erwähnt, dass wir im Zusammenhang mit komplexen Zahlen das Wurzelsymbol nicht verwenden. Würde man mit komplexen Zahlen und dem Wurzelzeichen rechnen, wie wir es von den reellen Zahlen gewohnt sind, dann würden wir auf Widersprüche der folgenden Art tre en:
√ √ » √
−1 = i2 = i i = −1 −1 = (−1)(−1) = 1 = 1.
Beispiel 11.8 (Wurzeln einer komplexen Zahl)
Wir bestimmen die 3-ten Wurzeln der komplexen Zahl |
|
|
Im |
|
|
|
|||||||||||||||||||||
a |
|
|
|
3 |
|
i. Dazu berechnen wir den Betrag % und |
a |
|
i |
z0 |
|
|
|||||||||||||||
den |
Winkel α von a: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
√ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= − |
|
|
√3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
5 π |
|
z1 |
|
5π |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ0 |
= 18 |
|
|
|||||
|
|
|
|
% |
= |
+ |
1 |
= |
2, |
α |
= |
arctan |
Πà |
3 |
|
π |
= |
6 . |
|
|
Re |
||||||
|
|
|
|
|
|
|
1 |
1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
‘ + |
|
|
|
|
− |
|
|
|
|||||||
Alle Wurzeln liegen auf einem |
Ursprungskreis mit Ra- |
|
|
|
|
|
|
||||||||||||||||||||
|
− |
|
|
|
|
|
|
|
|
|
√3 |
|
|||||||||||||||
dius r |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−i |
r = |
2 |
||||
= |
√2. Sie haben die Winkel |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
5 π |
|
|
|
5 π 2 π |
|
= |
5 π 2 π |
|
|
z2 |
|
|
|||||||||
|
|
|
|
ϕ0 = |
18 |
, ϕ1 |
= 18 |
+ |
3 , ϕ2 |
18 |
+2 |
3 . |
|
|
|
|
|
|
|||||||||
Die dritten Wurzeln der komplexen Zahl a |
|
√ |
|
i lassen sich daraus bestimmen. Sie lauten |
|
|||||||||||
|
3 |
Ì |
||||||||||||||
z0 = |
√2 e |
5 π |
, z1 = √2 e |
17 π |
, z2 = |
√2 e |
29 π |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 i |
18 |
3 i |
18 |
|
= − |
3 |
|
+i |
18 |
|
|
||||
Beim komplexen Wurzelziehen sind die selben Dinge wie bei einem Kindergeburtstag zu beachten. Zunächst muss man die Torte an der richtigen Stelle anschneiden. Dann ist es wichtig, dass jeder ein gleich großes Stück bekommt.
Bestimmung komplexer Wurzeln
Die n-ten Wurzeln einer komplexen Zahl a lassen sich wie folgt ermitteln:
(1) Stelle die komplexe Zahl a in Exponentialform dar: a = % ei α.
(2) |
Die erste Lösung z0 |
hat den Abstand |
√ |
|
vom Ursprung und den Winkel |
α |
: |
|
|
||||||||||
% |
n |
|
|
||||||||||||||||
|
z0 = |
√% e |
i |
n . |
|
|
|
n |
|
|
n |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Lösungen liegen gleichmäßig verteilt auf dem Ursprungskreis mit Radius |
|
|
: |
||||||||||||||
(3) |
Die |
√ |
% |
||||||||||||||||
|
√ |
|
|
|
α 2 k π |
|
|
|
|
|
|
|
|
|
|
|
|||
|
zk |
= |
% ei |
+n , |
k |
= |
0, 1, 2, . . . , n |
− |
1. |
|
|
|
|
|
|
||||
|
|
n |
|
|
|
|
|
|
|
|
|||||||||
Man kann die Formel zur Bestimmung der Lösungen der Gleichung zn |
= |
a aus Satz 11.13 |
||||||||||||
auch auf die Einheitswurzeln ω |
aus Satz 11.12 zurückführen: |
|
||||||||||||
|
|
|
|
|
α 2 k π |
|
|
k |
α |
2 k π |
|
|
|
|
zk |
= |
n |
% |
ei |
+n |
n |
% |
ei |
n ei |
n |
= |
z0 ωk. |
|
|
|
√ |
|
= √ |
|
|
|
|
|
||||||
