
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

245
6 Di erenzialrechnung
Die Di erenzialrechnung beschäftigt sich mit dem Änderungsverhalten einer Funktion. Ausgehend von einem bestimmten Funktionswert kann man mit Mitteln der Di erenzialrechnung über den weiteren Verlauf einer Funktion spekulieren. Di erenzialrechnung könnte man böswillig als mathematische Wahrsagerei bezeichnen. Tatsächlich hat das Thema jedoch wenig mit Esoterik zu tun. Bei der Di erenzialrechnung konzentriert man sich auf kleine Änderungen. Bei kleinen Änderungen in der Variablen lässt sich die Veränderung der Funktion sehr zuverlässig prognostizieren.
Wenn man beispielsweise von einem Fahrzeug, das mit hoher Geschwindigkeit auf der Autobahn fährt, die aktuelle Position und Geschwindigkeit kennt, dann kann man recht zuverlässig berechnen, an welcher Position sich das Fahrzeug 0.1 Sekunden später befinden wird.
Die Di erenzialrechnung ist ein unverzichtbares Hilfsmittel bei der mathematischen Modellbildung. Dabei versucht man, die Wirklichkeit durch Funktionen zu beschreiben. Bei Di erenzialgleichungen in Kapitel 12 werden wir das Thema Modellbildung noch genauer beleuchten.
6.1 Steigung und Ableitungsfunktion
Bei der Ableitung einer Funktion gibt es einen lokalen und einen globalen Aspekt. Der lokale Aspekt beschäftigt sich mit dem Steigungsverhalten der Funktion an einer bestimmten Stelle. Der globale Aspekt stellt den Zusammenhang zwischen der Funktion und ihrer Ableitungsfunktion her. Beide Aspekte werden in diesem Abschnitt betrachtet.
6.1.1 Tangente und Di erenzierbarkeit
Lokal kann man eine Funktion durch eine Gerade annähern. Dazu greift man zwei Punkte auf dem Schaubild der Funktion heraus und verbindet diese Punkte durch eine Gerade. Diese Gerade, die sogenannte Sekante, hat eine konstante Steigung. Die Steigung der Sekante wird als Di erenzenquotient bezeichnet und lässt sich mithilfe des Steigungsdreiecks ermitteln.

246 |
6 Di erenzialrechnung |
Definition 6.1 (Sekante, Di erenzenquotient)
Eine Sekante einer Funktion f ist eine Gerade durch zwei Punkte des Schaubildes von f. Das Verhältnis der Di erenzen der Funktionswerte und der x-Werte
m |
f |
( |
x1 |
) − |
f |
( |
x0 |
) |
= |
f |
|
|
|
|
|
|
|||||||
|
|
|
|
− |
|
|
|
|
|
||
= |
|
|
x1 |
x0 |
|
|
x |
||||
|
|
|
|
|
|
|
|||||
beschreibt die Steigung der Sekante
g(x) = f(x0) + m(x − x0)
und wird als Di erenzenquotient bezeichnet.
Beispiel 6.1 (Sekante)
y |
f(x) |
|
|
||
f(x1) |
|
g(x) |
|
|
|
|
|
f |
f(x0) |
x |
|
|
|
|
x0 |
x1 |
x |
Wir bestimmen die Sekante der Funktion |
y |
f (x) = 1 + 2x − 21 x2 |
|
|
||||||||||||||||||
|
f(x) = 1 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
||||||||
|
+ 2 x − 2 x |
|
|
|
|
|
3 |
|
|
|
x = 1 |
|
|
|||||||||
an den Stellen x0 |
|
|
3 und x1 |
|
4. Die Steigung m |
2 |
|
|
|
|
|
|
||||||||||
der Sekante |
ermitteln wir mit dem Steigungsdreieck |
|
|
|
|
f = |
3 |
|||||||||||||||
|
|
|
|
|
−2 |
|||||||||||||||||
|
|
|
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
( |
|
) − |
|
( ) = |
1 |
− |
5 |
|
|
1 |
|
|
|
|
|
|
||
|
|
= |
|
4 |
|
= − |
3 |
|
1 |
2 |
3 |
4 |
5 |
x |
||||||||
|
|
f |
f |
|
2 |
|
||||||||||||||||
|
m |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4 |
|
|
3 |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
Die |
Geradengleichung der Sekante lautet |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = |
5 |
− |
3 |
(x − 3). |
Ì |
|
2 |
|
2 |
||||
Wenn die beiden Punkte auf der Sekante nahe beieinanderliegen, dann unterscheidet sich die Sekante zwischen diesen beiden Punkten kaum von der Funktion. Deshalb definiert man die Steigung einer Funktion als Grenzwert der Sekantensteigung.
Definition 6.2 (Ableitung und Di erenzierbarkeit an der Stelle x0)
Der Grenzwert
f |
′( |
x0 |
) = |
lim |
f |
( |
x0 |
+ |
x |
) − |
f |
( |
x0 |
) |
|
|
→ |
|
|
|
|
|
|||||||
|
|
|
|
x 0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
heißt, falls er existiert, Ableitung der Funktion f an der Stelle x0. Man nennt dann die Funktion f di erenzierbar an der Stelle x0. Es sind verschiedene Schreibweisen gebräuchlich:
|
df |
|
|
f′(x0) = f˙(x0) = |
|
Vx0 |
= D fSx0 . |
dx |
|||
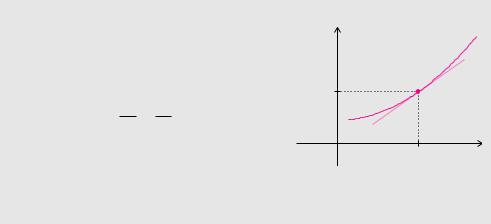
6.1 Steigung und Ableitungsfunktion |
247 |
Die Schreibweise für Ableitungen als Quotient der infinitesimal kleinen Größen df und dx geht auf Gottfried Wilhelm Leibniz zurück. Der große Vorteil dieser Di erenzialschreibweise liegt darin, dass man mit Di erenzialen formal rechnen darf wie mit anderen Variablen. Im Folgenden werden wir einige Rechenregeln und mathematische Eigenschaften auf einfache Weise mittels Di erenzialen herleiten. In Kapitel 7 werden wir genau diese Di erenzialschreibweise bei Integralen wieder antre en.
Etwa zeitgleich entwickelte Isaac Newton in England ebenfalls moderne Di erenzialrechnung. Auf ihn geht die heute hauptsächlich für die Ableitung nach der Zeit verwendete Notation f˙ zurück.
Einige Jahrzehnte später, Ende des 18. Jahrhunderts, führte Joseph-Louis Lagrange die heute weit verbreitete Standardschreibweise f′ ein.
Den Buchstaben D in Definition 6.2 bezeichnet man als Di erenzialoperator. Diese Operatorschreibweise wird gerne von Mathematikern verwendet und ist auch bei Computeralgebrasystemen üblich. Augustin-Louis Cauchy benutzte vorzugsweise die Operatorschreibweise Df.
Die Gerade, die beim Grenzübergang aus der Sekante entsteht, bezeichnet man als Tangente.
Definition 6.3 (Tangente, Di erenzialquotient) |
|
|
||||
Eine Tangente einer Funktion f ist eine Ge- |
y |
f(x) |
||||
rade durch einen Punkt des Schaubildes von f. |
|
|||||
|
|
|||||
Die Tangente berührt das Schaubild von f. Der |
|
g(x) |
||||
Grenzwert des Di erenzenquotienten |
|
|||||
f(x0) |
|
|||||
|
′( |
|
|
df |
|
|
f |
x |
lim f |
|
|
||
|
0) = |
x→0 x = |
dx Vx0 |
|
|
|
beschreibt die Steigung der Tangente |
x0 |
x |
||||
g(x) = f(x0) + f′(x0)(x − x0)
und wird als Di erenzialquotient bezeichnet.
Funktionswert und Steigung von Funktion und Tangente stimmen also überein. Ganz allgemein spricht man bei Schaubildern von Funktionen, die an einer Stelle x0 denselben Funktionswert und dieselbe Steigung haben, von sich berührenden Funktionen. Dabei handelt es sich jedoch um einen lokalen Sachverhalt. Eine Tangente berührt das Schaubild der Funktion an der Stelle x0. Es ist aber nicht gesagt, dass diese Tangente das Schaubild der Funktion nicht noch an anderen Stellen schneidet.
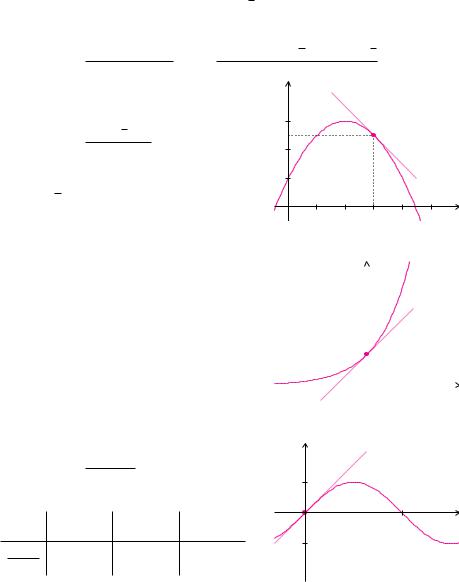
248 |
6 Di erenzialrechnung |
Beispiel 6.2 (Tangente)
a) |
Für die Tangente der Funktion f x |
|
|
1 |
|
|
2 x |
1 x2 an der Stelle x0 |
|
3 berechnen wir die |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
erenzialquotienten |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
Steigung mit dem Di |
|
|
|
|
( |
|
|
) = |
|
+ |
|
|
− |
|
1 |
|
|
= |
5 |
|
|
|
||||||||||||||
|
|
|
|
|
lim |
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
lim |
1 |
|
2 3 |
x |
3 |
x 2 |
|
|
|
|
|||||||
|
f |
′ 3 |
|
|
f |
|
|
|
x |
|
f |
|
|
|
|
|
|
|
|
|
2 |
( + ) − |
2 . |
|
|
|
|||||||||||
|
|
|
|
x |
→ |
0 |
|
( |
|
+ |
x |
|
( ) |
|
|
|
x |
→ |
0 |
|
|
+ ( + ) − x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
) − |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||||
|
Die |
meisten Terme kürzen sich weg und wir er- |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
( |
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
f (x) = 1 + 2x − 21 x2 |
|||||||||
|
halten |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
′(3) = |
lim |
|
|
|
x |
|
1 |
x2 |
= −1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||
|
f |
|
|
|
|
|
|
2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x→0 − −x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
Die Tangente hat die Steigung f′ |
( |
3 |
) = − |
1 und |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
lautet y |
= |
5 |
|
|
x |
− |
3 |
) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 − ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
5 |
x |
||||||
b)Die Funktion f(x) = ex hat an der Stelle x0 = 0 den Funktionswert f(0) = 1. Die Steigung der Tangente an dieser Stelle
|
|
f |
|
0 |
|
|
lim |
e x |
|
e0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
f (x) = ex |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
′( |
|
) = |
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
→ |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ermitteln wir aus den Näherungswerten: |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x |
|
|
0.1 |
|
|
0.01 |
|
0.001 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
e x |
|
|
1 |
1.05171 |
|
1.00502 |
|
1.00050 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
−1 |
|
|
1 |
2 |
x |
|||||||||||||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Der Grenzwert ist o ensichtlich 1 und die Tangente somit y 1 |
+ |
x. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
c) Die Steigung der Tangente des Sinus f |
x |
) = |
sin x an der Stelle=x0 |
0 führt auf den Grenzwert |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
lim sin |
|
− |
0 . |
y |
|
|
f |
′( |
0 |
) = |
x |
|
|
|
||||
|
|
x→0 |
x |
|
1 |
f (x) = sin x |
|
||||
Aus den Näherungswerten |
|
|
|
||||||||
|
x |
|
|
0.1 |
|
0.01 |
0.001 |
π |
x |
||
|
|
|
|
|
|
||||||
sin |
|
x |
|
|
|
|
|
−1 |
|
|
|
x |
0.99833 |
|
0.99998 |
0.99999 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
erkennen wir, dass dieser Grenzwert 1 ist. Somit lautet die Tangente y = x. |
Ì |
In Beispiel 6.2 haben wir die Steigung der Tangente etwas umständlich durch Grenzwerte berechnet. Ab Abschnitt 6.1.2 werden wir zur Berechnung der Steigung Ableitungsfunktionen verwenden, was die Sache wesentlich vereinfachen wird.
