Bei der Di erenzialrechnung werden wir in Abschnitt 6.2.1 das Prinzip der äußeren und inneren Funktion für die sogenannte äußere und innere Ableitung verwenden. Die Substitutionsregel der Integralrechnung in Abschnitt 7.3.2 basiert ebenfalls auf verketteten Funktionen.

Beispiel 5.20 (Komposition von Funktionen)

Die beiden Funktionen g(x) = 5 und h(x) = 1 − x können auf unterschiedliche Weise verkettet x

werden. Wendet man die Funktion g auf die Funktion h an, dann ergibt sich

In Beispiel 5.20 haben wir gesehen, dass es bei der Komposition von Funktionen auf die Reihenfolge ankommt. In der Sprechweise der Mathematiker ist die Komposition eine nicht kommutative Verknüpfung.

Komposition

Bei der Komposition von Funktionen ist die Reihenfolge entscheidend. In der Regel sind die beiden Funktionen g ○ h und h ○ g nicht identisch.

5.2 Polynome und rationale Funktionen

Rationale Funktionen lassen sich allein mithilfe der vier Grundrechenarten Addition, Subtraktion, Multiplikation und Division definieren. Nicht zuletzt aus diesem Grund werden rationale Funktionen bei technischen Anwendungen, wie etwa in der Regelungstechnik, gerne eingesetzt. Auch Polynome fallen unter den Begri rationale Funktionen, sie werden oft auch als ganzrationale Funktionen bezeichnet.

5.2.1 Potenzfunktionen mit ganzen Hochzahlen

Die einfachsten rationalen Funktionen sind die Potenzfunktionen mit ganzen Hochzahlen. Das Verständnis dieser Funktionen bildet die Basis für den weiteren Umgang mit rationalen Funktionen. Deshalb wollen wir die wesentlichen Eigenschaften dieser Potenzfunktionen an dieser Stelle nochmals zusammenfassen. Funktionen mit beliebigen reellen Hochzahlen betrachten wir in Abschnitt 5.6.

Definition 5.11 (Potenzfunktion mit ganzer Hochzahl)

Eine Funktion f, die sich in der Form

f(x) = a xn, n Z, a R

darstellen lässt, bezeichnet man als Potenzfunktion.

Potenzfunktionen verhalten sich unterschiedlich, je nachdem ob die Hochzahl gerade oder ungerade bzw. positiv oder negativ ist. Der konstante Faktor a bewirkt lediglich eine Skalierung der Funktionswerte, siehe Abschnitt 5.1.7.

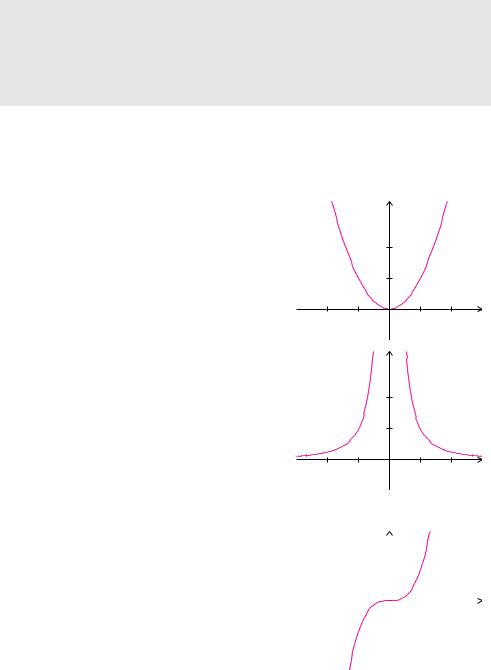
Beispiel 5.21 (Potenzfunktionen mit geraden Hochzahlen)

Beispiel 5.22 (Potenzfunktionen mit ungeraden Hochzahlen)

Potenzfunktion

Potenzfunktionen mit positiver Hochzahl sind für alle reellen Zahlen definiert, Potenzfunktionen mit negativer Hochzahl sind für alle reellen Zahlen mit Ausnahme der Null definiert. Das Schaubild einer Potenzfunktion mit gerader Hochzahl ist spiegelsymmetrisch zur y-Achse, das Schaubild einer Potenzfunktion mit ungerader Hochzahl ist spiegelsymmetrisch zum Ursprung.

5.2.2 Polynome

Polynome sind gewissermaßen die Lieblingsfunktionen der Mathematiker. Einerseits lassen sich mit Polynomen viele mathematische Operationen, wie beispielsweise das Di erenzieren und das Integrieren, problemlos durchführen. Andererseits haben Problemstellungen, wie etwa die Bestimmung der Nullstellen von Polynomen, zu interessanten mathematischen Theorien geführt.

Definition 5.12 (Polynom, ganzrationale Funktion)

Eine Funktion f, die sich in der Form

n

f(x) = a0 + a1x + a2x2 + a3x3 + . . . + anxn = Q ak xk, an ≠ 0,

k=0

darstellen lässt, bezeichnet man als Polynom oder ganzrationale Funktion vom Grad n. Die Koe zienten a0, a1, a2, a3, . . ., an sind dabei beliebige Zahlen, wobei allerdings der höchste Koe zient an nicht null sein darf.

Die sogenannte triviale Funktion f(x) = 0 ist aufgrund der Forderung an ≠ 0 laut Definition 5.12 streng genommen kein Polynom. Trotzdem werden wir auch die triviale Funktion als Polynom zulassen. Somit sind alle konstanten Funktionen f(x) = c Polynome. Außerdem sind alle linearen Funktionen f(x) = mx + b und alle quadratischen Funktionen f(x) = ax2 + bx + c Polynome. Einzelheiten zu linearen und quadratischen Funktionen findet man in Abschnitt 1.5.1 und Abschnitt 1.5.3.

Aus der Schulmathematik ist uns die Darstellung von Polynomen wie in Definition 5.12 so vertraut, dass man andere Darstellungsmöglichkeiten von Polynomen leicht übersieht. Insbesondere zur Lösung praktischer Probleme ist es oft von Vorteil, Polynome in anderer Form darzustellen. Dazu stehen etwa die nach den Mathematikern Sergei Natanowitsch Bernstein, Joseph-Louis Lagrange und Sir Isaac Newton benannten Polynome zur Verfügung. Details sind in [Schwarz] oder [Mohr:Numerik] zu finden.

Polynome sind durch ihre Koe zienten definiert. Somit sind zwei Polynome genau dann gleich, wenn alle entsprechenden Koe zienten übereinstimmen. Das klingt nach einer Binsenweisheit. Wir werden diesen Sachverhalt, den man Koe zientenvergleich nennt, jedoch an vielen Stellen gewinnbringend einsetzen.

Satz 5.1 (Koe zientenvergleich)

Die beiden Polynome

f(x) = a0 + a1x + a2x2 + . . . + anxn, g(x) = b0 + b1x + b2x2 + . . . + bnxn

sind genau dann identisch, wenn alle ihre entsprechenden Koe zienten identisch sind:

a0 = b0, a1 = b1, a2 = b2, . . . , an = bn.

Polynome lassen sich addieren und subtrahieren, indem man einfach die entsprechenden Koe zienten addiert bzw. subtrahiert. O ensichtlich ergibt die Multiplikation zweier Polynome wieder ein Polynom. Dabei entsteht bei der Multiplikation eines Polynoms vom Grad n mit einem Polynom vom Grad m ein Polynom vom Grad n + m.

Satz 5.2 (Multiplikation von Polynomen)

Die Multiplikation eines Polynoms vom Grad n mit einem Polynom vom Grad m ergibt ein Polynom vom Grad n + m.

Die Berechnung der Koe zienten des Produktpolynoms erfordert zwar etwas Sorgfalt, die generelle Methode lässt sich jedoch auch ohne großen Formalismus aus den folgenden Beispielen erkennen. Wem diese Vorgehensweise zu pragmatisch erscheint, der findet im Abschnitt 8.4 unter dem Begri Cauchy-Produkt weitere Informationen zum Thema Multiplikation von Potenzreihen.

b)Durch geschicktes Umformen mithilfe der dritten binomischen Formel ergibt sich für das Polynom f(x) = (x2 + x + 1)(x2 + x − 1) die neue Darstellung

Die Eigenschaften linearer und quadratischer Polynome lassen sich mithilfe elementarer Methoden, die bereits aus der Schulmathematik bekannt sind, untersuchen. Die wichtigste Eigenschaft von Polynomen von höherem Grad besteht darin, dass sie sich in Produkte aus linearen und quadratischen Polynomen zerlegen lassen. Diese Zerlegung erfolgt mithilfe der sogenannten Polynomdivision. Die Polynomdivision ist gewissermaßen die Umkehrung der Multiplikation von Polynomen. Sie verläuft analog zu der üblichen Division von Zahlen mit Rest.

Satz 5.3 (Polynomdivision)

Bei der Polynomdivision teil man das Polynom f vom Grad n durch das Polynom g vom Grad m und erhält dann ein neues Polynom h vom Grad n−m und eventuell noch ein Restpolynom r:

f(x) g(x) = h(x) + r(x) g(x).

Grundsätzlich ist eine Polynomdivision nur dann sinnvoll, wenn der Grad m des Nennerpolynoms g nicht größer als der Grad n des Zählerpolynoms f ist.

Durch Multiplikation der Gleichung mit g(x) ergibt sich f(x) = h(x)g(x) + r(x). Besonders hilfreich sind Polynomdivisionen, die ohne Rest aufgehen, denn dann hat man das Polynom f(x) in die beiden Faktoren g(x) und h(x) zerlegt.

Satz 5.4 (Polynomdivision ohne Rest)

Wenn die Polynomdivision f(x) g(x) = h(x) ohne Rest aufgeht, dann hat man das Polynom f in ein Produkt der beiden Polynome g und h zerlegt:

f(x) = g(x) h(x).

Polynomdivision ist nichts anderes als ein mathematisches Rechenverfahren, das wir in Form eines Algorithmus formulieren könnten. An dieser Stelle wollen wir darauf jedoch verzichten und die prinzipielle Vorgehensweise lediglich an ein paar Beispielen illustrieren.

ergibt sich die Zerlegung

x3 − 6x2 + 11x − 6 = ‰x2 + 3x + 2Ž (x − 9) + 36x + 12.

b) Die Polynomdivision

‰x3 − 6x2 + 11x − 6 Ž ‰x2 − 3x + 2Ž = x − 3

Die Nullstellen von linearen und quadratischen Polynomen lassen sich ohne großen Aufwand bestimmen. Auch für Polynome vom Grad 3 existieren die nach Gerolamo Cardano benannten Cardanischen Formeln. Beiträge dazu stammen bereits aus dem 16. Jahrhundert von dem venetianischen Mathematiker Niccolò Fontana Tartaglia. Für Polynome vom Grad 4 existieren ebenfalls Lösungsformeln. Viele Mathematiker haben vergeblich versucht, Lösungsformeln für die Nullstellen von Polynomen von beliebigem Grad zu finden, bis Niels Henrik Abel und Évariste Galois Anfang des 19. Jahrhunderts nachgewiesen haben, dass es für die Nullstellen von Polynomen mit Grad größer gleich 5 keine allgemeine Formel geben kann.

Deshalb versucht man, Polynome von höherem Grad in Produkte aus Polynomen vom Grad n ≤ 2 zu zerlegen. Diese Zerlegung gelingt mit Polynomdivision, vorausgesetzt man kennt ein geeignetes lineares oder quadratisches Polynom, sodass die Division ohne Rest aufgeht.

Teilt man ein Polynom p durch ein lineares Polynom der Bauart g(x) = (x−x0), dann lässt sich wegen f(x) = h(x)(x − x0) + r(x) sehr schnell erkennen, unter welchen Umständen diese spezielle Polynomdivision ohne Rest aufgeht. Wenn nämlich x0 eine Nullstelle von f ist, dann muss auch r(x0) = 0 gelten.

Definition 5.13 (Linearfaktor)

Falls x0 eine Nullstelle des Polynoms f vom Grad n ist, geht die Polynomdivision

Beispiel 5.26 (Polynomdivision durch Linearfaktoren)

a) Da x0 = 1 eine Nullstelle des Polynoms x3 − 6x2 + 11x − 6 ist, muss die Polynomdivision

‰x3 − 6x2 + 11x − 6 Ž ‰x − 1Ž = x2 − 5x + 6

−x3 + x2

−5x2 + 11x

5x2 − 5x

6x − 6

− 6x + 6 0

ohne Rest aufgehen und wir erhalten die Zerlegung

x3 − 6x2 + 11x − 6 = ‰x2 − 5x + 6Ž (x − 1) .

b) x0 = −2 ist keine Nullstelle des Polynoms x3 − 6x2 + 11x − 6. Die Polynomdivision

−8x2 + 11x

8x2 + 16x

27x − 6

−27x − 54

−60