
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

236 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 Funktionen |
|||
Beispiel 5.80 (Bisektion) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Wir suchen Lösungen der Gleichung 2 e− |
x |
|
= |
x |
|
|
|
|
|
|
y |
f (x) = 2e−x |
|
8 |
|
||||||||||||
|
|
8 . Dazu |
|
|
1 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
x |
|
||
bilden wir die stetige Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f(x) = 2 e−x − |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
4 |
x |
||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||
und suchen die |
Nullstellen |
dieser Funktion. Durch |
|
− |
a˜0 |
|
|
|
|
˜ |
|||||||||||||||||
|
|
|
|
|
|
|
b0 |
||||||||||||||||||||
Abschätzen kann man feststellen, dass f für x |
|
1 |
|
|
|
a˜1 |
|
˜ |
|
|
|
||||||||||||||||
|
|
|
|
|
b1 |
|
|
|
|||||||||||||||||||
positiv und für |
x |
4 |
negativ |
ist. Nach |
Satz |
5.21 |
|
|
|
|
|
˜ |
|
|
|
||||||||||||
|
|
|
= |
|
|
|
|
a˜2 |
|
b2 |
|
|
|
||||||||||||||
|
einer stetigen Funktion hat f also |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
über die Nullstellen= |
|
|
|
|
|
|
[ |
1, 4 |
] |
. |
|
|
|
|
|
|
|
a˜3 |
|
˜b3 |
|
|
|
||||
mindestens eine Nullstelle im Intervall |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Für das Startintervall |
|
1, 4 |
] |
gilt also |
|
|
|
|
|
( |
|
0) ≈ −0 4634 |
|
|
|
|
|
|
|
||||||||
a˜0 = 1, |
b0 = 4[, |
|
(˜0) ≈ 0 6108 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
˜ |
|
|
f |
a |
. |
|
|
|
, |
|
|
f |
˜ |
|
. |
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||||||
|
Š |
|
|
+ |
|
|
|
• < |
|
˜ |
|
|
a˜0 ˜b0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
|
|
|
|
|
|
|
||||||||
Nun ist f |
a˜0 |
|
˜ |
|
|
0, also setzen wir |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
b0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a˜1 |
|
|
a˜0 |
|
|
|
1, |
|
|
b1 |
|
|
|
|
|
|
|
|
2.5, |
f |
|
a˜1 |
|
|
0.6108, |
|
f |
|
b1 |
|
|
|
0.1483. |
|
|
|
|||||||||
= |
|
= |
|
|
= |
+ |
|
|
|
( |
) ≈ |
|
|
) ≈ − |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= a˜1 ˜b1 |
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
˜b1 |
|
|
|
|
|
2 |
|
|
|
Š |
+ |
• > |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
a˜1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ein zweiter Schritt liefert wegen f |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
= |
|
|
|
|
+ |
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
2 |
|
|
|
( ) ≈ |
|
|
|
|
|
( ) ≈ − |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a˜2=˜b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
a˜2 |
|
|
|
|
|
|
|
|
|
|
|
1.75, |
|
|
˜ |
|
|
|
˜ |
2.5, |
|
f a˜2 |
|
|
0.1288, |
|
|
|
˜ |
|
|
|
0.1483. |
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
b2 |
|
|
b1 |
|
|
|
|
f |
|
b2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ein dritter Schritt liefert wegen f |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Šb2 |
2 |
• < |
|
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
˜ |
|
|
|
|
|
|
|
|
|
˜ |
a˜2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a˜3 |
|
|
b3 |
|
|
|
1.75, |
|
b3 |
|
|
|
|
+ |
˜ |
2.125, |
|
|
f |
a˜3 |
0.1288, |
|
f b3 |
0.0268. |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Die Nullstelle= |
liegt= |
im Intervall= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fort,) ≈ −kann man eine Kon- |
|||||||||||||||||||||
|
1.75,=2.125 . Führt( man) ≈ das Verfahren( |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
langsame, gegen die exakte Nullstelle beobachten. Für n |
|
30 etwa |
|||||||||||||||||||||||||
vergenz, wenn auch eine recht |
|
[ |
|
|
|
|
|
] |
|
|
|
|
|
|
|
|
a˜30 |
˜ |
|
|
|
|
|
Näherungs- |
|||||||||||||||||||||
ist der Mittelpunkt |
x˜30 2.053192717488855 |
des Intervalls |
|
, b30 |
|
ein recht guter |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Die ersten 10 Nachkommastellen sind bereits korrekt. |
|
|
Ì |
|||||||||||||||||||||||||||||
wert für die Nullstelle. = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
|
|
|
|
|
] |
|
|
|
|
|
|||||||||||||||
5.9 Anwendungen
Funktionen sind in der Modellierung technischer Sachverhalte allgegenwärtig. Jede Abhängigkeit einer Ausgangsgröße von einer Eingangsgröße kann als Abbildung und somit zumindest abschnittsweise auch als Funktion aufgefasst werden. Allerdings nimmt man in den meisten Anwendungen gleichzeitig auch Ergebnisse der Di erenzialrechnung zu Hilfe, siehe Kapitel 6.
5.9.1 Messwerte
Bei vielen Anwendungen aus der Praxis kennt man keine explizite Funktionsgleichung. Oft kennt man lediglich ein paar Funktionswerte, die durch Messungen im Versuch er-

5.9 Anwendungen |
237 |
mittelt wurden. Aus diesen Messwerten lassen sich auf unterschiedliche Arten Funktionen erzeugen. Die einfachste Methode ist die sogenannte lineare Interpolation.
Lineare Interpolation
Bei der linearen Interpolation definiert man |
y |
|
n = 6 |
||||||||||||||||||
eine stetige und stückweise lineare Funktion |
|
|
|
||||||||||||||||||
durch die Punkte |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x0 f0 , x1 f1 , x2 f2 , . . . , xn fn , |
|
|
|
||||||||||||||||||
indem(manS |
dem) ( |
x-SWert) (im SIntervall) |
x , x |
) |
|
|
|
||||||||||||||
( |
|
S |
|
|
|
||||||||||||||||
den Funktionswert |
|
|
|
|
|
|
[ |
k |
|
k+1] |
x0 x1 x2 x3 |
x4 |
x5 x6 x |
||||||||
|
|
|
|
|
|
|
|
fk 1 |
fk |
|
|
|
|
|
|
|
|
|
|||
f |
|
x |
|
|
fk |
|
|
|
x |
|
xk |
|
|
|
|
|
|
|
|
||
( |
) = |
+ |
xk+1 |
− xk |
( |
− |
) |
|
|
|
|
|
|
|
|||||||
|
|
|
+ |
− |
|
|
|
|
|
|
|
|
|
||||||||
zuordnet. Dabei sind die x-Koordinaten aufsteigend sortiert: x1 < x2 < . . . < xn. |
|||||||||||||||||||||
Man kann die Formel für die lineare Interpolation auch für x-Werte außerhalb des Intervalls [xk, xk+1] verwenden. Dann spricht man aber nicht mehr von Interpolation, sondern von Extrapolation.
Beispiel 5.81 (Wertetabelle)
Bei einem Motor wurde zu verschiedenen Drehzahlen das Drehmoment experimentell bestimmt. Die diskreten Werte sind in der Tabelle festgehalten.
Drehzahl |
[min−1] |
2000 |
3000 |
4000 |
5000 |
6000 |
7000 |
8000 |
9000 |
Drehmoment |
[Nm] |
30 |
37 |
45 |
50 |
52 |
50 |
38 |
25 |
Um nun das Drehmoment bei einer beliebigen Drehzahl zwischen 2000 und 9000 Umdrehungen pro Minute zu bestimmen, werden die Werte linear interpoliert. Um beispielsweise das Drehmoment bei der Drehzahl 2200 Umdrehungen pro Minute zu bestimmen, betrachtet man das passende Teilintervall [2000, 3000] und berechnet dann den Wert durch
|
|
|
|
|
37 |
− |
30 |
|
|
|
|
|
|
|
f |
( |
2200 |
) = |
30 |
+ |
3000 |
2000 |
( |
2200 |
− |
2000 |
) = |
31.4. |
|
Dadurch |
|
|
|
− |
|
|
|
|
||||||
|
entsteht eine Funktion, die über den ganzen |
|
||||||||||||
Drehzahlbereich von 2000 bis 9000 Umdrehungen pro Minute definiert ist. Der Verlauf des Drehmomentes in Abhängigkeit der Drehzahl lässt sich dadurch veranschaulichen, dass man die diskreten Werte durch Geradenstücke verbindet. Im technischen und naturwissenschaftlichen Bereich ist es üblich, bei der Beschriftung einen gemeinsamen Skalierungsfaktor, wie bei uns der Faktor 103, zusammen mit der Variablen als Beschriftung der Achse zu wählen.
y 
80
70
60
50
40
30
20
10
2 3 4 5 6 7 8 9 x · 103 Ì
238 |
5 Funktionen |
Neben der linearen Interpolation gibt es noch eine ganze Reihe weiterer Verfahren, mit denen man Funktionen aus diskreten Werten bestimmen kann. Abhängig davon, ob das Schaubild der Funktion exakt oder nur näherungsweise durch die vorgegebenen Punkte verläuft, spricht man von einem Interpolationsoder Approximationsverfahren. Weitere Details findet man in Kapitel 10 und Kapitel 13.
5.9.2 Industrieroboter
Die Bahnkurven von Industrierobotern lassen sich mathematisch über Funktionen darstellen. Diese Bahnkurven müssen so berechnet werden, dass der Greifarm mit keinem Teil der Produktionsanlage und keinem Werkstück unbeabsichtigt kollidiert. Diese Bedinung legt in der Regel eine Bahnkurve noch nicht eindeutig fest. Deshalb nutzt man die verbleibenden Freiheitsgrade, um, je nach Anwendung, zeitoptimal, energieoptimal oder verschleißoptimal zu steuern.
Beispiel 5.82 (Zweiarmroboter)
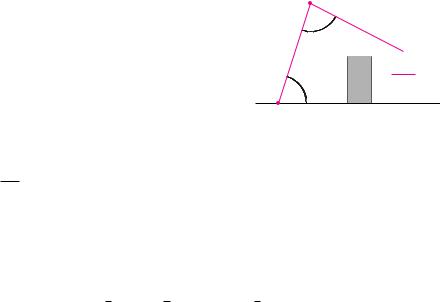
Wir betrachten einen Roboter mit zwei Armen gleicher Länge s in der Ebene, der im Ursprung aufgestellt ist. Bei gegebenen Winkeln α und β ergeben sich die Positionen der Gelenke zu O = (0 S 0) und
P |
|
s |
|
cos α |
|
, Q |
|
P |
|
s |
|
cos α |
+ |
β |
|
. |
= |
Π|
sin α |
‘ |
= |
− |
Π|
sin(α |
β) |
‘ |
|||||||
|
|
|
|
|
|
( |
+ |
) |
|
Damit ist insbesondere die Greifposition Q als Endpunkt der beiden Arme bekannt.
P
βs
Q s 

O α
Bei der Steuerung des Roboters stellt sich allerdings häufig das inverse Problem: Welche Gelenkwinkel α und β müssen eingestellt werden, damit ein gegebener Punkt Q(x S y) auf einer vorgegebenen Bahnkurve, siehe dazu auch Abschnitt 9.1, erreicht wird? Da die beiden Arme gleich lang sind, bildet OQP ein gleichschenkliges Dreieck. Bezeichnet M den Mittelpunkt der Strecke OQ = 2a, so sind die Dreiecke OMP und MQP rechtwinklig. Für die Winkel im rechtwinkligen Dreieck MQP gilt also
|
a |
|
β |
a |
|
|||||
α1 = (P QM) = arccos |
|
, |
|
|
= (MP Q) = arcsin |
|
. |
|
|
|
s |
2 |
s |
|
|||||||
Den Ergänzungswinkel α2 von α1 zu α erhält man durch α2 = arctan |
y |
. Insgesamt ergibt sich |
||||||||
|
|
|||||||||
x |
||||||||||
α = α1 + α2 = arccos a + arctan y , s x
β = 2 arcsin a. s
Wir sehen, dass bei dieser inversen Kinematik gerade die inversen trigonometrischen Funktionen die zentrale Rolle einnehmen. Allerdings ist dabei generell auch etwas Vorsicht geboten. Obige
Formeln gelten sicher für die Winkelbereiche α |
|
0, π2 |
|
und β |
|
0, π . Da die Umkehrfunktio- |
||
nen einen begrenzten Definitionsund |
Wertebereich haben, muss man für größere Gelenkwinkel |
|||||||
|
|
|
|
|
[ |
] |
Ì |
|
Fallunterscheidungen durchführen. |
|
|
|
|
|
|
|
|
