
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

12.7 Anwendungen |
519 |
12.7 Anwendungen
Di erenzialgleichungen werden in vielen Bereichen der Naturwissenschaften und der Technik angewendet. In diesem Abschnitt haben wir eine kleine Auswahl von Anwendungen zusammengestellt, die jeweils typische Aspekte beinhalten und gleichzeitig nur ein überschaubares Wissen in den einzelnen Fachgebieten erfordern.
12.7.1 Temperaturverlauf
Ein Körper mit einer Anfangstemperatur T0 befindet sich in einem umgebenden Medium mit konstanter Temperatur T . Aus der Physik ist bekannt, dass die Temperaturänderung des Körpers proportional zur Temperaturdi erenz ist. Beschreibt T (t) die Temperatur des Körpers zur Zeit t, und ist k > 0 die Proportionalitätskonstante, so gilt die Di erenzialgleichung erster Ordnung
dT = −k(T − T ). dt
Diese lineare Di erenzialgleichung mit konstanten Koe zienten hat die homogene Lösung
Th(t) = Ce−k t.
Eine partikuläre Lösung erhält man durch Variation der Konstanten zu
|
Tp t |
e k t |
|
k T |
t |
dt T |
|
|
|
|
|
T t |
Th t Tp t |
T |
|
|
Ce k t. |
||||||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
||
|
|
|
|
e k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) Anfangsbedingung= |
=T 0 |
|
|
T |
|
T |
|
( ) = |
|
|
+ |
|
|||||||||
Mittels |
|
Ôlässt( ) = |
( ) + |
|
|
|
|||||||||||||||||
der |
|
S |
|
|
allgemeinen |
|
0 |
T0 |
|
|
|
|
|
|
|||||||||
sich |
die |
Konstante |
C |
der |
Lösung |
|
|
|
|
|
|
||||||||||||
|
|
|
|
( |
|
) = |
|
|
|
|
|
|
|
|
|
||||||||
T t |
bestimmen und lautet C |
|
T0 |
|
|
T . Somit |
|
T (t) |
|
|
|
|
|||||||||||
die Lösung des Problems gegeben durch |
|
|
|
|
|
|
|
||||||||||||||||
ist( ) |
|
|
|
|
|
|
|
= |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
T t T |
T0 T |
e−k t |
|
|
|
|
|
|
|
|
Tp(t) |
|
|
|
|
|
||||||
Dabei spielt( ) =es keine+ ( |
Rolle,− )ob T0 |
|
größer oder |
T |
|
|
|
|
|
|
|||||||||||||
kleiner als T ist. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|||
12.7.2 Radioaktiver Zerfall
Wir betrachten ein radioaktives Präparat, das zur Zeit t = 0 die Anzahl N(0) = N0 radioaktive Kerne hat. Einzelne radioaktive Atomkerne zerfallen völlig zufällig. Da es sich aber um eine sehr große Anzahl von Kernen handelt, betrachtet man eine Zerfallswahrscheinlichkeit pro Zeiteinheit. Diese Zerfallswahrscheinlichkeit wird üblicherweise durch die Halbwertszeit ausgedrückt. Die Halbwertszeit gibt an, nach welcher Zeit durchschnittlich die Hälfte der ursprünglichen radioaktiven Kerne zerfallen sind. Abhängig von der

520 |
12 Gewöhnliche Di erenzialgleichungen |
Substanz kann die Halbwertszeit Sekundenbruchteile oder Milliarden Jahre betragen. Die Zerfallsgeschwindigkeit N˙ ist immer proportional zur Anzahl der radioaktiven Teilchen. Es gilt also die lineare Di erenzialgleichung erster Ordnung mit konstanten Koe zienten
dN = −λN. dt
Zur Bestimmung der Anzahl der radioaktiven Teilchen zur Zeit t müssen wir eine Funktion N bestimmen, die diese Gleichung erfüllt und zur Zeit t = 0 den Wert N(0) = N0 hat. Die Lösung dieses Anfangswertproblems ist gegeben durch
N(t) = N0 e−λ t.
Die Halbwertszeit t bestimmt man aus
N |
t |
) = |
1 |
N0 |
Ô |
N0 e |
λ t |
= |
|
1 |
N0 |
Ô − |
λ t |
= |
ln |
1 |
|
Ô |
t |
= |
ln 2 |
. |
2 |
2 |
|
|
|||||||||||||||||||
( |
|
|
− |
|
|
|
2 |
|
λ |
|||||||||||||
In unserem Modell ist die Halbwertszeit t unabhängig von der ursprünglichen Anzahl N0.
12.7.3 Freier Fall mit Luftwiderstand
Einen freien Fall mit Luftwiderstand erlebt man beispielsweise beim Fallschirmoder Bungee-Springen. Aber auch das Eindringen eines Meteoriten in die Erdatmosphäre fällt in diese Kategorie der Bewegungsbeschreibung. Durch die Erdanziehungskraft mit Erdbeschleunigung g wird die Masse m beschleunigt. Andererseits bremst der Luftwiderstand den Fall. Wir betrachten die Luftreibung nicht proportional zur Geschwindigkeit v, sondern proportional zum Quadrat der Geschwindigkeit. In der Physik spricht man dabei von Viskose-Reibung. Aus dem Kräftegleichgewicht ergibt sich die Bewegungsgleichung:
m v˙ + k v2 − m g = 0.
Dabei wird die Bewegung nach unten durch negative Geschwindigkeitswerte v angegeben. Die Konstante k hängt von der Querschnittsfläche A und dem Widerstandsbeiwert cw des Körpers, aber auch von der Dichte ρ der Luft ab:
1
k = 2 cw A ρ.
Sofern alle Parameter unabhängig von der Zeit sind, wird das Problem durch eine nichtlineare Di erenzialgleichung erster Ordnung beschrieben. Diese Di erenzialgleichung ist separierbar:
m |
dv |
= m g − k v2 |
Ô |
S |
m |
dv = S |
dt. |
dt |
m g − k v2 |
Eine explizite Formel für v lässt sich mithilfe einer Partialbruchzerlegung durch elementare Stammfunktionen berechnen. Siehe dazu auch Aufgabe 12.24.

12.7 Anwendungen |
521 |
12.7.4 Feder-Masse-Schwinger
Unter einem Feder-Masse-Schwinger, auch Federschwinger oder Federpendel genannt, versteht man eine Versuchsanordnung mit einer Feder mit Federkonstante c. Die Masse m des Systems stellt man sich idealisierter Weise konzentriert in einem einzigen Punkt vor. Reibungseinflüsse werden nur proportional zur Geschwindigkeit berücksichtigt und durch eine Dämpfungskonstante k angegeben. In der Physik spricht man dabei von Stokes-Reibung. Das System kann an der Aufhängung der Feder von außen angeregt werden. Das Verhalten des Feder-Masse-Schwingers wird durch den zeitlichen Verlauf der Auslenkung x der Masse beschrieben. In Ruhelage definieren wir den Nullpunkt der Auslenkung, Positionen oberhalb der Ruhelage haben eine Auslenkung x 0 und Auslenkungen unterhalb der Ru-
helage haben eine Auslenkung x 0. Zum Zeitpunkt t |
|
0 erzwingen wir die Auslenkung |
||||||||||||
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
x 0 |
|
x |
0 |
. Wenn sich die Masse in Bewegung setzt, dann haben wir die Anfangsgeschwin- |
||||||||||
|
|
|
|
|
v . |
< |
|
= |
|
|
|
|
|
|
digkeit x˙ 0 |
|
|
|
|
|
|
|
|
|
|||||
( ) = |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
dem Hookeschen Gesetz ist die Auslenkung |
|
|
|
|
|
|
|||||||
Nach |
|
|
( |
) = |
|
|
|
|
|
F(t) |
|
|
||
|
|
|
|
|
|
|
|
|||||||
einer Feder annähernd proportional zur einwir- |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
kenden Kraft: |
|
|
|
|
|
|
|
|
c |
|||||
|
|
FF = −c x. |
|
|
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||||||
x(t)
Reibung berücksichtigen wir proportional zur Ge-
k
schwindigkeit
FR = −k x˙.
Außerdem kann eine Kraft F von außen wirken.
Nach dem Newtonschen Gesetz werden diese Kräfte durch das Produkt aus Masse m und Beschleunigung x¨ kompensiert:
F m x¨ |
mx¨ |
+ |
kx˙ |
+ |
cx |
= |
F |
t |
) |
. |
|
|
|
Wenn es =uns alsoÔ |
|
|
|
|
|
( |
|
|
|
||||
gelingt, eine Funktion x zu bestimmen, die diese Gleichung erfüllt |
|||||||||||||
und zum Zeitpunkt t |
0 den Wert x 0 |
|
|
x0 sowie die Anfangsgeschwindigkeit x˙ 0 |
|
v0 |
|||||||
|
|
|
|
|
Schwingung mathematisch beschreiben. Aus mathe- |
||||||||
besitzt, dann können=wir damit die ( ) = |
|
|
|
( |
) = |
|
|||||||
matischer Sicht ist der Feder-Masse-Schwinger eine Schwingungsdi erenzialgleichung:
x¨ |
|
k x˙ |
|
c |
x |
|
F t |
. |
|
|
+ |
|
|
+ |
|
|
= |
( |
) |
|
m |
m |
|
||||||
|
|
|
|
|
|
|
|
m |
|
¯¯ ²
2 δ |
ω2 |
r t |
|
|
0 |
Anregung um eine harmonische Anregung handelt, können wir die |
|
Sofern es sich bei der |
|||
( ) |
|||
Methoden aus Abschnitt 12.4 anwenden und die Lösung mathematisch beschreiben. Das mathematische Modell des Feder-Masse-Schwingers hat vielfältige Anwendungsgebiete. In der Automobilindustrie wird das Schwingungsverhalten am sogenannten Viertelfahrzeug untersucht. In der Computergrafik verwendet man den Feder-Masse-Schwinger, um realitätsnahe Bewegungsabläufe zu simulieren. In der Medizin werden Feder-Masse- Systeme zur Simulation operativer Eingri e eingesetzt.

522 12 Gewöhnliche Di erenzialgleichungen
12.7.5 Pendel
Wir betrachten eine Masse m, die sich im Abstand l von einem Drehpunkt befindet. Auf die Masse wirkt die Erdanziehungskraft mit Erdbeschleunigung g. Oft spricht man in diesem Zusammenhang von einem Fadenpendel. Für unsere Betrachtungen ist es jedoch zweckmäßiger, wenn die Masse durch eine starre Stange mit dem Drehpunkt verbunden ist. Dadurch können wir auch Bewegungen mit Überschlägen, wie bei einer Schi schaukel, berücksichtigen. Wir lassen nur Bewegungen innerhalb einer Ebene zu. Außerdem gehen
wir davon aus, dass die Masse in einem Punkt konzentriert ist. |
|
|
||
Unter diesen idealisierten Annahmen erhalten |
|
|
||
wir die Bewegungsgleichung des mathematischen |
|
|
||
Pendels m ` x¨ |
|
m g sin x. Unter Berücksichti- |
|
|
gung von Stokes-Reibung mit dem Faktor k, also |
x(t) |
` |
||
|
= − |
|
||
Reibung proportional zur Geschwindigkeit, ergibt |
|
|
||
sich |
|
|
|
|
m ` x¨ + k x˙ |
+ m g sin x = 0. |
|
m |
|
|
|
|||
In beiden Fällen handelt es sich um eine nichtlineare Di erenzialgleichung zweiter Ordnung. Ohne Berücksichtigung von Reibung kann man das Prinzip der Energieerhaltung anwenden und Gleichungen für die Phasenkurven in der x-x˙-Ebene herleiten.
Unter Berücksichtigung von Reibung ist das Problem nicht mehr elementar lösbar. Man kann sich dann auf sehr kleine Auslenkungen beschränken. Die Linearisierung sin x ≈ x ergibt dann eine Schwingungsdi erenzialgleichung
m ` x¨ + k x˙ + m g x = 0,
die wir mit den Methoden aus Abschnitt 12.4 analysieren können. Falls man sich nicht auf kleine Auslenkungen beschränken kann, ist man auf numerische Näherungslösungen angewiesen, siehe Abschnitt 12.6.2. Der Verlauf der Lösungskurven in der Phasenebene orientiert sich an den Gleichgewichtspunkten, siehe Abschnitt 12.5.5.
12.7.6 Wechselstromkreise
Aus Sicht der Mathematik muss man zwischen zwei Arten elektrischer Stromkreise unterscheiden. Bei Gleichstromkreisen bleibt die Stärke und die Richtung der Spannungen und Ströme zeitlich konstant. Die einzelnen Spannungen und Ströme in einem Gleichstromkreis lassen sich durch lineare Gleichungssysteme berechnen, siehe Abschnitt 2.5.2.
In Wechselstromkreisen verändert sich die Stärke und die Richtung der Spannungen und Ströme mit der Zeit. Spannungen und Ströme sind in diesem Fall also Funktionen der Zeit. Auch in Wechselstromkreisen gelten, unter bestimmten Einschränkungen, die Kirchho schen Gesetze, siehe Abschnitt 2.5.2. Für unsere Betrachtung genügt das 2. Kirchho sche Gesetz. Nach diesem Gesetz, der sogenannten Maschenregel, ist die Summe aller Teilspannungen in einer Masche null. In einem Wechselstromkreis betrachtet man neben Widerständen auch Spulen und Kondensatoren.
12.7 Anwendungen |
|
|
|
|
|
|
|
|
|
|
|
|
523 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wechselstromkreis |
) |
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
Wechselstromkreis gilt zwischen Wechselspannung u t |
und Wechselstrom i t |
||||||||||||
Im an einem Widerstand mit Ohmschem Widerstand R:( |
u t |
|
R i t , |
( |
||||||||||
L |
|
|
( ) = |
|
1 d(t ) |
|
||||||||
L |
an einer Spule mit Induktivität L: |
|
u(t) = L |
d(i)t |
|
, |
|
|
||||||
|
|
|
|
|
||||||||||
L |
an einem Kondensator mit Kapizität C: |
|
u t |
|
|
|
q |
t |
|
. |
|
|
|
|
|
|
( |
) = |
|
|
|
( |
|
) |
|
|
|
|
|
|
|
C |
|
|
|
|
||||||||
|
|
|
|
|
|
dq t |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
Dabei gilt zwischen der Ladung q(t) und dem Strom i(t) die Beziehung |
|
|
d(t ) |
= i(t). |
||||||||||
Durch die Zusammenhänge zwischen Wechselspannung und Wechselstrom ergeben sich aus den Kirchho schen Gesetzen Di erenzialgleichungen. In der Regel sind diese Di erenzialgleichungen oder Di erenzialgleichungssysteme linear. Weitere Einzelheiten zu Themen aus der Elektrotechnik findet man beispielsweise bei [Küpfmüller].
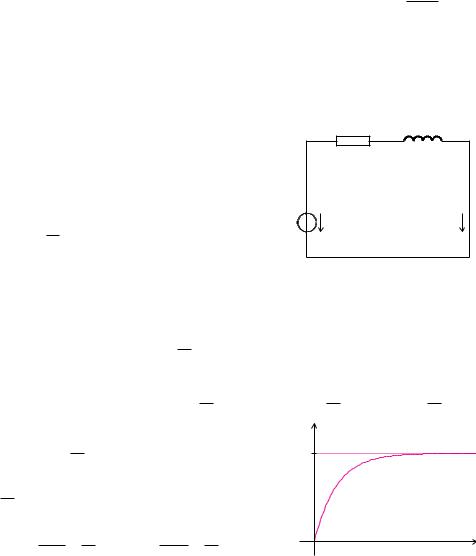
Beispiel 12.52 (RL-Schaltkreis) |
|
|
|
|
Wir betrachten den abgebildeten Schaltkreis mit ei- |
|
|
||
nem Ohmschen Widerstand R, einer Spule mit Induk- |
R |
L |
||
tivität L und einer angelegten Spannung u t . Der |
|
|||
|
|
|||
Schaltkreis besteht aus einer einzigen Masche, in der |
|
|
||
|
|
( ) |
|
|
nach dem 2. Kirchho schen Gesetz die Summe der |
|
|
||
Spannungen null ist: |
|
|
|
|
L di |
|
|
u(t) |
i(t) |
R i u t . |
|
|
|
|
dt |
+lineare= Di( )erenzialgleichung erster Ord- |
|
|
|
Dies ist eine |
|
|
||
nung mit konstanten Koe zienten. |
|
|
t K e− RL t, |
|
Die allgemeine Lösung der homogenen Gleichung können wir sofort angeben: ih |
||||
( ) =
mit einer Konstanten K. Partikuläre Lösungen sind abhängig von der angelegten Spannung u(t). Bei konstanter Spannung u(t) = U0 erhalten wir durch den Ansatz ip(t) = I0:
|
|
R I0 |
U0 |
|
|
ip t |
|
U0 . |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
Die Konstante= K könnenÔ wir(aus) =dem Anfangswert i 0 |
) = |
0 ermitteln: |
|
|
||||||||||||||||||
|
|
i t ih t ip t K e− |
RL t |
|
U0 |
|
|
( |
|
|
U0 |
|
|
U0 |
||||||||
|
|
|
|
|
R |
|
|
i 0 |
|
K |
|
R |
|
K |
R . |
|||||||
Somit |
lautet die Lösung |
|
|
|
|
+ |
Ô |
( |
) = |
|
+ |
|
Ô |
|
= − |
|||||||
( ) = |
( ) + |
( ) = |
|
|
|
i |
|
|
||||||||||||||
|
|
|
|
U0 |
|
R t |
|
|
|
|
|
|
|
|
U0 |
|
|
ip(t) |
|
|
||
|
|
i t |
|
|
1 |
e− L . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
R |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||||
Für t |
( |
) strebt= Šder− Strom• i gegen den Grenzwert |
|
|
|
|
|
i(t) |
|
|
||||||||||||
U0 |
Die Anfangssteigung zum Zeitpunkt t |
|
0 der |
|
|
|
|
|
|
|
|
|||||||||||
R . |
|
→ ∞ |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
Stromstärke i erhalten wir aus |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
i t |
U |
R |
|
i |
|
|
U |
|
|
|
|
|
|
|
|
|
|
|||
|
|
dd(t ) |
= L0 e− L t |
Ô d d(t0) |
= L0 . |
|
|
|
|
|
|
|
|
|
t Ì |
|||||||

524 |
12 Gewöhnliche Di erenzialgleichungen |
Beispiel 12.53 (RLC-Schwingkreis)
Im abgebildeten Schaltkreis befindet sich ein Ohm- |
|
|
|
|
|
|||||||
scher Widerstand R, ein Kondensator mit Kapazität |
|
R |
|
L |
|
|||||||
C und eine Spule mit Induktivität L in Reihe. Au- |
|
C |
|
|||||||||
|
|
|
||||||||||
ßerdem ist eine Spannung u t |
angelegt. Nach dem |
|
|
|
|
|
||||||
|
|
|
|
die Summe der Span- |
|
|
|
|
|
|||
2. Kirchho schen Gesetz ist( ) |
|
|
|
|
|
|
|
|
||||
nungen in der Masche null: |
|
|
|
|
|
|
|
|
|
|||
d i |
|
|
1 |
|
|
|
|
|
u(t) |
|
i(t) |
|
|
|
|
|
|
|
|
|
|
|
|
||
L dt |
+ R i + C q = u(t). |
|
|
|
|
|
|
|
|
|||
Diese Gleichung enthält neben der Stromstärke und |
|
|
|
|
|
|||||||
deren erster Ableitung auch noch die Ladung. |
|
|
|
|
|
|
|
|||||
Deshalb leiten wir die Gleichung nach t ab und ersetzen die Ableitung der Ladung durch die |
||||||||||||
Stromstärke. Nach Division mit L erhalten wir eine Schwingungsdi erenzialgleichung: |
|
|||||||||||
d2 i |
di |
1 |
du t |
d2 i |
|
R di |
1 |
du t |
|
|||
L dt2 |
+ |
R dt C i |
= |
d(t ) |
dt2 |
+ |
L dt L C i |
d(t ) . |
|
|||
|
|
+ |
Ô |
|
2 δ |
+ ω02 |
= r t |
|
|
|||
|
|
|
|
|
|
|
|
¯ |
± |
´¹¹¹¹¹¹¸¹¹¹¹¹¹¶ |
|
|
Es handelt sich also um ein schwingungsfähiges System, bei dem die |
Frequenz maßgeblich durch |
|||||||||||
( ) |
|
|||||||||||
das Produkt aus L und C bestimmt wird. In der Elektrotechnik spricht man deshalb von einem |
||||||||||||
L C-Glied. Unter Vernachlässigung des Ohmschen Widerstands R kann Resonanz auftreten. |
Ì |
|||||||||||
Beispiel 12.54 (Kettenleiter) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ein Schaltkreis mit zwei Maschen enthält zwei Ohm- |
|
|
|
|
|
|
|
||||||||||||||||||
sche Widerstände R1, R2 und zwei Spulen mit In- |
|
i1(t) |
L1 |
i2 |
(t) |
L2 |
|
||||||||||||||||||
duktivitäten L1 und L2. In der ersten Masche ist eine |
|
|
|
|
|||||||||||||||||||||
Spannung u t |
angelegt. In den beiden Maschen flie- |
|
|
|
|
|
|
|
|||||||||||||||||
ßen die |
Ströme i1 |
t |
|
und i2 |
|
t |
. Die Orientierung der |
|
I |
|
|
|
II |
|
|||||||||||
|
( ) |
jeder Masche festgelegt, siehe Pfeile |
|
|
|
|
|
|
|
||||||||||||||||
Ströme wird in |
|
|
( ) |
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
in der Abbildung. Dabei ist zu beachten, dass der Wi- |
|
u(t) |
R1 |
|
|
R2 |
|
||||||||||||||||||
derstand R1 zu beiden Maschen gehört und nur die |
|
|
|
|
|
|
|
||||||||||||||||||
Di erenz der beiden Maschenströme eine Spannung |
|
|
|
|
|
|
|
||||||||||||||||||
an diesem Widerstand erzeugt. Nach dem 2. Kirch- |
|
|
|
|
|
|
|
||||||||||||||||||
ho schen Gesetz ist die |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Summe der Spannungen in jeder Masche null: |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
L1 |
di1 |
t |
) |
|
|
|
R1 i1 t |
i2 t |
|
|
|
|
u t |
I |
|
|
|
|
||||||
|
|
d( |
|
+ |
|
|
|
( ( ) − ( )) |
|
|
= |
( ) ( ) |
|
|
|
|
|||||||||
|
|
di2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
d( ) + |
R1 |
|
|
i2 |
t |
i1 |
t |
|
|
R2 i2 |
t |
0 |
II |
|
|
|
|
||||||
|
|
|
|
|
( ( ) − |
( )) + |
|
( ) = |
|
( ) |
|
|
|
|
|||||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Der Kettenleiter lässt sich also durch ein lineares Di erenzialgleichungssystem mit konstanten |
|||||||||||||||||||||||||
Koe zienten beschreiben, das wir in Matrixform darstellen können: |
|
|
|
|
|
||||||||||||||||||||
|
dt |
|
|
|
R1 |
|
|
|
R1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
’ |
−L2 |
|
|
|
L2 |
“ |
’ |
u |
) “ |
|
|
|
|
|
|
|
|
|||||||
|
di |
|
|
L1 |
|
|
|
L1 |
|
t |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
. |
|
|
|
|
|
|
|
||||
|
|
= ” |
|
|
|
|
|
− |
|
+ |
|
i |
+ ” |
|
|
• |
|
|
|
|
|
|
|
||
|
|
|
R1 |
|
|
R1 |
R2 |
• |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Die Lösung dieses Systems lässt sich mit den Methoden aus Abschnitt 12.5.3 berechnen. |
Ì |
||||||||||||||||||||||||
