Die Formeln für die Fourier-Koe zienten lassen sich auch rein reell, also ohne die komplexe Darstellung, herleiten. Die Grundlage dafür bilden die sogenannten Orthogonalitätseigenschaften der trigonometrischen Funktionen, siehe [Heuser:FA]. Funktionen mit Orthogonalitätseigenschaften sind in der Funktionalanalysis, einem wichtigen Teilgebiet der Mathematik, von zentraler Bedeutung.

Im Zusammenhang mit der Minimaleigenschaft der Fourier-Koe zienten steht eine interessante, nach Marc-Antoine Parseval benannte Gleichung, die eine enge Beziehung zwischen dem Integral über eine Funktion und der Summe ihrer Fourier-Koe zienten beschreibt. Eine analoge Gleichung gilt auch für die Fourier-Transformation, siehe Satz 15.17.

Satz 13.5 (Parsevalsche Gleichung für Fourier-Reihen)

13.3 Eigenschaften

Mit den Formeln aus Satz 13.2 bzw. Satz 13.4 sind wir im Prinzip in der Lage, zu jeder periodischen Funktion eine Fourier-Reihe zu bestimmen. Die Bestimmung von Fourier-Rei- hen führt über die Integralrechnung. Wir können also Eigenschaften der Integralrechnung bei der Berechnung der Fourier-Koe zienten ausnutzen. Außerdem müssen wir das Rad nicht jedes Mal neu erfinden, sondern können Fourier-Reihen aus bereits bekannten Fou- rier-Reihen ermitteln. Eine Zusammenstellung von Fourier-Reihen wichtiger Funktionen findet sich im Anhang A.6.

13.3.1 Symmetrie

Die Berechnung von Fourier-Reihen beruht in der Standardnotation ohne Verschiebung auf Integralen, deren Integrationsbereich symmetrisch zum Ursprung sind. Bei geraden bzw. ungeraden Funktionen ist auch der Integrand symmetrisch zum Ursprung. Dadurch lassen sich die Berechnungen vereinfachen, siehe Satz 7.9.

Ein typisches Beispiel für eine gerade Funktion ist die Dreieckfunktion aus Beispiel 13.6. Das Schaubild ist achsensymmetrisch zur y-Achse. Die Funktionsgleichung erfüllt die Bedingung f(−t) = f(t), siehe Definition 5.17. Die Vorgehensweise aus Beispiel 13.6 lässt sich auf alle geraden Funktionen verallgemeinern.

13.3.3 Mittelwert

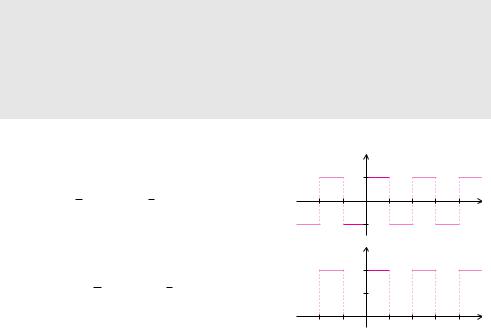
Wenn wir zu einer periodischen Funktion f einen konstanten Wert addieren, dann hat diese Änderung keine Auswirkung auf das eigentliche Schwingungsverhalten. Lediglich der Gleichanteil ändert sich. Wenn m der Mittelwert der Funktion f ist, dann hat die Funktion f˜(t) = f(t) + C den Mittelwert m˜ = m + C. Somit gilt für a˜0 die Beziehung

Mittelwert

Die Fourier-Reihe der Funktion f˜(t) = f(t) + C hat, abgesehen vom Gleichanteil, dieselben Fourier-Koe zienten ak, bk und ck wie die Funktion f mit Periode T . Für den Gleichanteil von f˜ gilt

a˜0 = a0 + 2 C, c˜0 = c0 + C.

Alle anderen Fourier-Koe zienten von f˜ stimmen mit den entsprechenden Koe zienten von f überein. Ì

13.3.4 Linearität

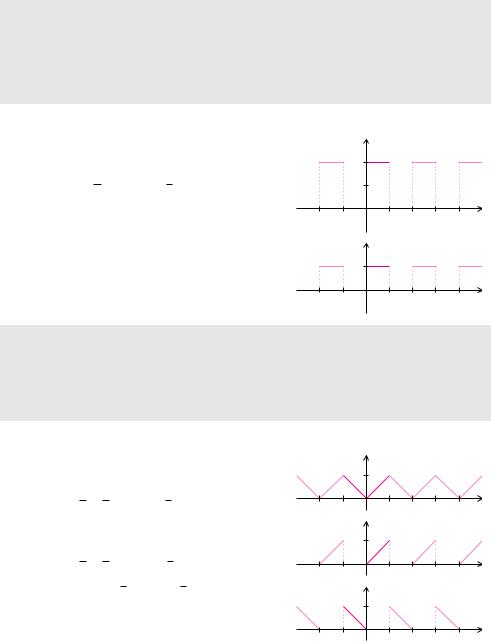
Die Linearität von Fourier-Reihen beantwortet zwei Fragen: Welche Fourier-Reihe hat die Überlagerung von zwei Funktionen mit derselben Periode und welche Auswirkung hat die Skalierung der Funktionswerte einer Funktion? Aus mathematischer Sicht sind diese beiden Fragen einfach zu beantworten, denn Integrale sind linear. Steht unter dem Integral eine Summe von Funktionen, so kann man das Integral in eine Summe von Integralen zerlegen. Einen konstanten Faktor kann man vor das Integral ziehen.

Skalierung

Bei der Fourier-Reihe der Funktion f˜(t) = C f(t) werden die Fourier-Koe zienten der Funktion f mit Periode T mit dem Faktor C multipliziert:

˜

a˜k = C ak, bk = C bk, c˜k = C ck.

Addition

Wenn die Funktion f3 aus der Überlagerung zweier Funktionen f1 und f2 mit derselben Periode T entsteht, also f3(t) = f1(t) + f2(t), dann bestimmt man die FourierKoe zienten der Funktion f3 durch Addition der Koe zienten der beiden Funktionen f1 und f2.