
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
7.4 Länge, Flächeninhalt und Volumen |
329 |
7.4.3 Rotationskörper
Einige Werkzeugmaschinen in der Zerspantechnik, wie beispielsweise die Drehmaschine, erzeugen Werkstücke in Form von Rotationskörpern. Mathematisch kann man solche Körper durch Rotation einer Kurve um eine Achse beschreiben. Wir gehen dabei davon aus, dass die Profilkurve und die Rotationsachse in derselben Ebene liegen und dass die Profilkurve die Rotationsachse nicht schneidet, sondern höchstens berührt. Unser Ziel in diesem Abschnitt ist es, Formeln zur Berechnung des Volumens und der Oberfläche eines Rotationskörpers zu bestimmen. Zur Vereinfachung der Formeln legen wir uns dabei auf die x-y-Ebene fest. Außerdem betrachten wir nur Rotation um volle 360○, sodass ein geschlossener Körper entsteht.
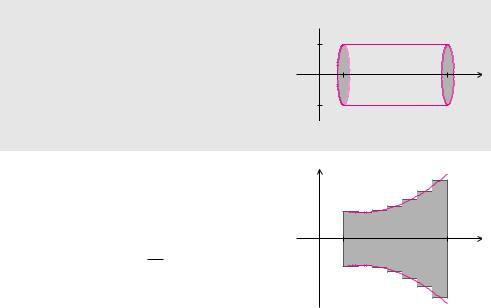
Der einfachste Rotationskörper ist ein senkrechter Kreiszylinder. Er entsteht durch Rotation einer zur x-Achse parallelen Geraden. Der Begri „senkrecht“ bezieht sich dabei auf den rechten Winkel zwischen der Rotationsachse und dem Boden und Deckel des Kreiszylinders und nicht etwa auf die Orientierung in der x-y-Ebene. Sein Volumen berechnet man aus dem Produkt des Flächeninhalts der Grundfläche und der Höhe. Die Grundfläche besteht aus einer Kreisscheibe mit Radius r und hat den Flächeninhalt A = π r2. Die Mantelfläche des senkrechten Kreiszylinders wird aus einem Rechteck mit den Seitenlängen b − a und 2 π r gebildet. Dies können wir uns klar machen, indem wir uns vorstellen, den Kreiszylinder entlang einer Geraden parallel zur Rotationsachse aufzuschneiden. Die Schnittkante hat die Länge b − a, der Umfang der Kreise beträgt 2 π r.
Satz 7.16 (Senkrechter Kreiszylinder)
Durch Rotation des Schaubildes der konstanten Funktion f(x) = r für x-Werte zwischen a und b um die x-Achse, entsteht ein senkrechter Kreiszylinder. Dieser Kreiszylinder hat das Volumen und die Mantelfläche
V = π r2(b − a), M = 2 π r (b − a).
y  r
r
a |
b |
x |
|
−r
Ausgehend von der Volumenformel für den senk- |
y |
|
|
|||
rechten Kreiszylinder können wir uns eine Formel |
|
f(x) |
|
|||
für das Volumen eines allgemeinen Rotationskör- |
|
|
|
|||
pers herleiten. Dazu zerlegen wir den Körper in |
|
|
|
|||
eine Summe von n Kreiszylindern. Alle Zylinder |
|
|
x |
|||
haben dieselbe Höhe |
x |
= |
− |
a |
b |
|
|
b a , nur die Radien fk |
|
|
|
||
|
|
|
n |
|
|
|
der Kreisscheiben sind abhängig vom Funktionswert. Wir wählen als Radius den Funktionswert in der Mitte des jeweiligen Teilintervalls:
fk = f ‰a + k x − 12 xŽ , k = 1, 2, . . . , n.
330 7 Integralrechnung
Für das Volumen Vx des Rotationskörpers erhalten wir somit die Näherungsformel
n
Vx ≈ π f12 x + π f22 x + . . . + π fn2 x = π Q fk2 x.
k=1
Aus dieser Näherungsformel ergibt sich beim Grenzübergang für n gegen unendlich die gesuchte Formel.
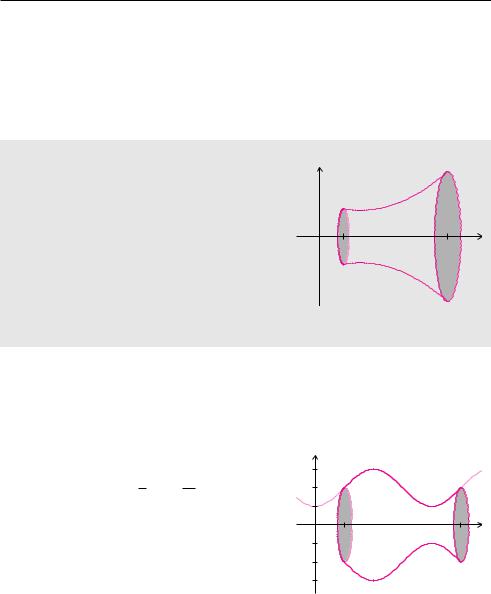
Satz 7.17 (Volumen bei Rotation um die x-Achse)
Durch Rotation des Schaubildes einer stetigen |
y |
|
|
|
Funktion f für x-Werte zwischen a und b um |
|
f(x) |
|
|
die x-Achse entsteht ein Rotationskörper. Das |
|
|
|
|
Volumen dieses Rotationskörpers kann man |
|
|
|
|
mit der Formel |
|
a |
b |
x |
|
|
|||
Vx = π Sa |
b |
|
||
|
|
|
||
f(x)2 dx |
|
|
|
|
berechnen. Dabei darf das Schaubild der Funktion f die x-Achse nicht schneiden, sondern höchstens berühren.
Die Formel für das Volumen einer Rotationsfläche kann man sich einfach merken. Eine Rotationsfläche besteht aus lauter Kreisscheiben. Jede Kreisscheibe hat die Fläche π r2, wobei der Radius r bei einer Rotationsfläche durch den Funktionswert gegeben ist. Das Aufsummieren erfolgt durch das Integral.
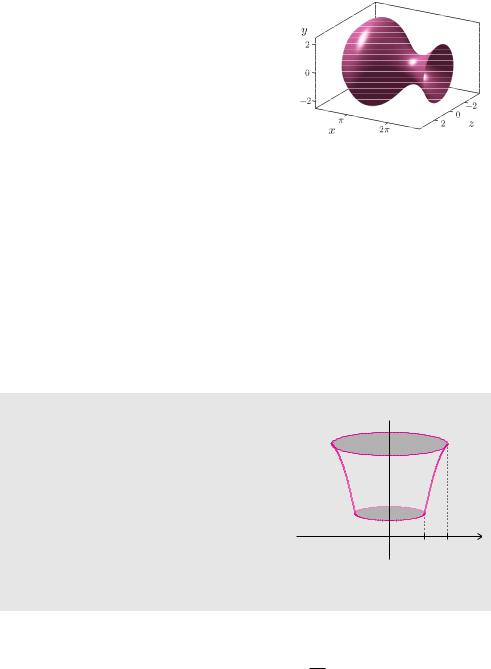
Beispiel 7.33 (Volumen bei Rotation um die x-Achse)
Durch Rotation des Schaubildes der Funktion |
y |
|
|
f (x) = 2 − cos x |
|||||||||||
f(x) = 2 − cos x, |
π |
|
5π |
3 |
|
|
|||||||||
|
1 |
|
|
|
|
|
|||||||||
2 ≤ x ≤ 2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
um die x-Achse entsteht ein amphorenähnlicher Ro- |
|
|
|
|
|
|
|||||||||
tationskörper. Das Volumen dieses Körpers berechnet |
|
1 |
π |
5 |
π |
x |
|||||||||
sich mit der Formel |
|
|
|
|
|
|
−1 |
2 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
52 |
|
|
|
|
|
|
− |
|
|
|
|
|
|
= |
|
π |
( |
2 |
− |
cos x |
) |
2 dx. |
2 |
|
|
|
|
|
Vx |
π |
π |
3 |
|
|
|
|
|
|||||||
|
|
S2 |
|
|
|
− |
|
|
|
|
|
||||
Zur Berechnung des Integrals multiplizieren wir die Klammer aus und berechnen die Teilintegrale einzeln:
|
= |
|
S |
5π |
− |
|
S |
5π |
+ |
|
S |
5π |
Vx |
π |
2 4 dx |
4 π |
2 cos x dx |
π |
2 cos2 x dx. |
||||||
|
|
2 |
|
2 |
|
2 |
||||||
|
|
|
|
π |
|
|
|
π |
|
|
|
π |
|
|
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|||
|
|
|
|
V1 |
|
|
|
V2 |
|
|
|
V3 |
7.4 Länge, Flächeninhalt und Volumen |
331 |
Das erste Teilintegral entspricht der Fläche eines Rechtecks mit Grundseite 2 π und Höhe 4, der Wert ergibt also V1 = 8 π. Beim zweiten Integral wird der Kosinus über eine komplette Periode integriert. Daraus folgt V2 = 0. Beim dritten Teilintegral nutzen wir die Symmetrie zwischen Sinus und Kosinus aus. Es gilt nämlich
Sπ |
5π |
cos2 x dx = Sπ |
5π |
2 |
2 sin2 x dx |
22
und somit
|
= S2 |
5π |
= |
1 |
S2 |
5π |
‰ |
|
+ |
|
|
= |
1 |
S2 |
|
V3 |
2 cos2 x dx |
2 |
cos2 x |
sin2 x |
dx |
||||||||||
|
|
|
|
||||||||||||
2 |
|
2 |
|||||||||||||
|
|
|
|
|
Ž |
||||||||||
|
π |
|
|
|
π |
|
|
|
|
|
|
|
|
|
π |
Insgesamt erhalten wir Vx = 8 π2 + π2 = 9 π2.
5π
2 1 dx = π.
Ì
Unsere Überlegungen lassen sich auf Rotationen um die y-Achse übertragen. Allerdings müssen wir sicherstellen, dass ein und derselbe y-Wert nicht als Funktionswert von zwei unterschiedlichen x-Werten im Intervall [a, b] vorkommt. Funktionen, die diese Eigenschaften erfüllen, kennen wir bereits. Es sind die umkehrbaren Funktionen, siehe Definition 5.53. Die Radien der Kreisscheiben sind nun die Funktionswerte der Umkehrfunktion f−1. Die Summation läuft nun im Bereich zwischen f(a) und f(b). Allerdings könnte nun auch f(b) kleiner als f(a) sein. In diesem Fall wäre die Untergrenze des Integrals f(b) und die Obergrenze f(a). Beide Fälle lassen sich mithilfe des Betrags zu einer Formel zusammenfassen.
Satz 7.18 (Volumen bei Rotation um die y-Achse)
Durch Rotation des Schaubildes einer stetigen Funktion f für x-Werte zwischen a und b um die y-Achse entsteht ein Rotationskörper. Wenn die Funktion f auf dem Intervall [a, b] umkehrbar ist, dann kann man das Volumen dieses Rotationskörpers mit der Formel
Vy = π WS f(b) ‰f−1(x)Ž2 dxW
f(a)
y 
f(x)
a b x
berechnen. Dabei darf das Schaubild der Funktion f die y-Achse nicht schneiden, sondern höchstens berühren.
Bei der Rotation um die y-Achse lässt sich das Volumen auch ohne die Bestimmung der Umkehrfunktion berechnen. Dazu verwendet man die Substitution u = f−1(x) bzw.
f(u) = x. Mit dem Verhältnis der Di erenziale f′(u) = dx folgt
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
Vy |
= |
π |
f(b) |
‰ |
f |
1 |
x |
2 dx |
π |
WSa |
b u2 f |
′ |
u du |
W = |
π |
Sa |
b u2 |
S |
f |
′( |
u |
)S |
du. |
|
|
WSf(a) |
|
− |
( )Ž |
W = |
|
|
( ) |
|
|
|
|
|
|||||||||
332 |
7 Integralrechnung |
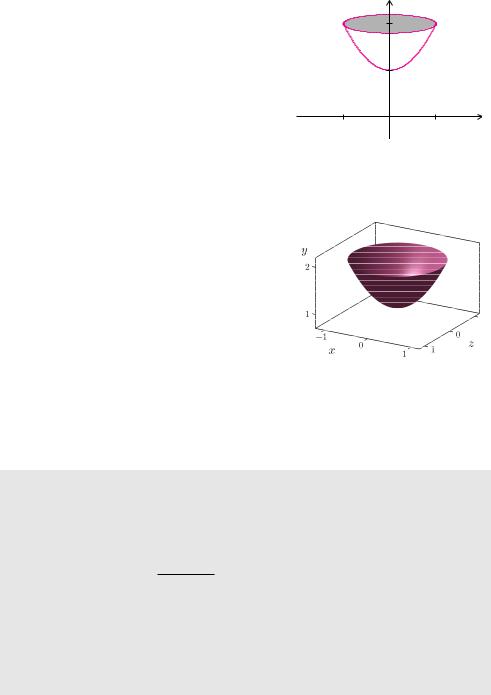
Beispiel 7.34 (Volumen bei Rotation um die y-Achse)
Das Schaubild der um 1 in Richtung der positiven |
y |
|
|
||||||||
y-Achse verschobenen Normalparabel |
2 |
|
|
||||||||
f x |
|
x2 1 |
|
|
|
|
|
|
|
|
|
mit x-Werten( ) =zwischen+ |
0 und 1 wird um die y-Achse |
1 |
f (x) = x2 + 1 |
||||||||
rotiert. Das Volumen können wir mit folgender For- |
|
|
|
||||||||
mel berechnen: |
|
|
|
|
|
|
|
|
|||
Vy |
= |
π |
f(b) |
f |
− |
1 x |
2 dx. |
−1 |
1 |
x |
|
|
|
Sf(a) |
‰ |
|
( )Ž |
|
|
|
|||
Dazu benötigen wir die Funktionsgleichung der Umkehrfunktion f−1. Diese bestimmen wir durch Auflösen der Funktionsgleichung von f nach y:
|
|
|
|
|
|
x2 |
|
1 |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
» |
|
|
|
. |
|
|
|
|
|
|
|
|
|
y |
= |
+ |
|
|
|
|
|
= |
y |
− |
|
|
x |
y |
− |
1 |
|
|
|
|
|
||||||||||||||||
Wir |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||
|
vertauschen die Variablen x und y und erhal- |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
( |
) = |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) = |
|
|
|
|
|
|
|
|
|
|
|
||||
ten f−1 |
x |
− |
1. Mit den Grenzen f |
a |
1 und |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
f b |
|
2 ergibt sich |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
( ) = |
|
Vy = π |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 2 Š√x − 1• dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
= |
π |
S |
x |
− |
1 |
) |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Sx2 |
( |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= π Œ |
|
− x‘W1 = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Alternativ dazu können wir die Lösung auch mit der Formel |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
x2 Tf′(x)T dx = π S0 |
1 |
|
|
|
|
|
|
|
1 |
x |
4 |
1 |
π |
||||||||||||||||
|
|
|
Vy = π S0 |
|
|
|
x2 |
S2 xS dx = π S0 2 x3 dx = π |
|
W0 = |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
2 |
|||||||||||||||||||||||||||||||||
berechnen. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
||||||
Satz 7.19 (Mantelfläche)
Durch Rotation des Schaubildes einer di erenzierbaren Funktion f für x-Werte zwischen a und b um
L die x-Achse entsteht ein Rotationskörper mit Mantelfläche
b »
Mx = 2 π S f(x) 1 + f′(x)2 dx.
a
L die y-Achse entsteht ein Rotationskörper mit Mantelfläche
My |
|
2 π |
|
f fa(b) f |
1 |
x ½ |
|
|
|
|
|
|
|
|
|
|
. |
= |
WS |
1 |
+ ( |
f |
1 |
( |
x |
))′ |
2 dx |
W |
|||||||
|
|
( ) |
− |
( ) |
|
|
− |
|
|
|
|
||||||
