
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
557
14 Verallgemeinerte Funktionen
Die Steuerung technischer Geräte basiert oftmals auf sehr einfachen Prinzipien. Beipielsweise wird eine Heizung oder ein elektrischer Fensterheber zu einem gewissen Zeitpunkt t0 eingeschaltet und dann zu einem späteren Zeitpunkt t1 wieder ausgeschaltet. Aus mathematischer Sicht handelt es sich dabei um eine Funktion, die im Intervall [t0, t1] den Wert 1 hat und sonst überall null ist. Verblü enderweise bereiten solche Funktionen den Mathematikern mehr Kopfzerbrechen, als man auf den ersten Blick vermutet. Die Hauptproblematik ist die fehlende Di erenzierbarkeit bei Funktionen mit Sprungstellen. In diesem Kapitel werden wir neue Darstellungsformen für derartige Funktionen kennenlernen. Wir werden den klassischen Ableitungsbegri so erweitern, dass wir in Zukunft auch Funktionen mit Sprungstellen di erenzieren können. Außerdem werden wir das Prinzip der Faltung kennenlernen. Die Inhalte dieses Kapitels sind grundlegend für das Verständnis der Fourier-Transformation in Kapitel 15 und der Laplace-Transformation in Kapitel 16.
14.1 Heaviside-Funktion
Die Heaviside-Funktion beschreibt einen Sprung der Höhe 1 an der Stelle t = 0. Man bezeichnet die Heaviside-Funktion σ auch als Einheitssprungfunktion. Für negative t- Werte sind die Funktionswerte null und für positive t-Werte konstant 1.
Definition 14.1 (Heaviside-Funktion)
Die abschnittsweise definierte Funktion
σ |
t |
) = œ |
0 |
für |
t |
< |
0 |
1 |
für |
t |
0 |
||||
|
( |
|
|
|
≥ |
|
bezeichnet man als Heaviside-Funktion oder
Einheitssprungfunktion.
σ(t) |
|
1 |
|
1 |
t |
Beispiel 14.1 (Heaviside-Funktion)
a) Eine Verschiebung der Heaviside-Funktion
σ(t − t0)
erzeugt einen Sprung an der Stelle t0. Positive t0-Werte bewirken eine Verschiebung nach rechts, negative eine Verschiebung nach links.
1 |
σ(t − t0) |
t0 |
t |
−1 |
|

558 |
14 Verallgemeinerte Funktionen |
b) |
Die Heaviside-Funktion |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
σ t |
t1 |
|
(t |
|
t |
) |
|
hat−eine( −Sprungstelle) |
|
|
||||
|
bei t1. Für alle t-Werte grö- |
−σt1 |
− |
1 |
t |
||
|
ßer als t1 hat sie den Funktionswert −1. |
−1 |
|
|
Ì |
||
Der Funktionswert der Heaviside-Funktion an der Stelle t = 0 ist für unsere Betrachtungen unerheblich. In der Literatur findet man die Varianten σ(0) = 0, σ(0) = 1 und σ(0) = 12 . Die Heaviside-Funktion kann man sich als einen Einschaltvorgang zum Zeitpunkt t = 0 vorstellen.
Durch Kombination der beiden Funktionen aus Beispiel 14.1 kann man eine Rechteckfunktion erzeugen. In Anlehnung an die Physik bezeichnet man diese Funktion auch als Rechteckimpuls. Sie ist für alle t-Werte kleiner als t0 und größer als t1 null. Zwischen diesen beiden Werten hat sie den konstanten Funktionswert 1. Der Rechteckimpuls beschreibt einen Vorgang, der zum Zeitpunkt t0 startet und zum Zeitpunt t1 endet.
Definition 14.2 (Rechteckimpuls)
Die Funktion
r(t) = σ(t − t0) − σ(t − t1)
beschreibt einen Rechteckimpuls, der zur Zeit t0 beginnt und zur Zeit t1 endet.
r(t) |
|
|
1 |
|
|
t0 |
t1 |
t |
Beispiel 14.2 (Dreieckfunktion)
Die abgebildete Dreieckfunktion lässt sich mithilfe von zwei Rechteckfunktionen darstellen. Das erste Rechteck startet bei t = −1, endet bei t = 0 und wird mit der Geraden g1(t) = 1 − t multipliziert. Das zweite Rechteck startet bei t = 0, endet bei t = 1 und wird mit der Geraden g2(t) = 1 + t multipliziert. Insgesamt ergibt sich
g1(t) = 1−t |
g2(t) = 1+t |
|
|
1 |
|
|
s(t) |
|
−1 |
1 |
t |
( ) = ( |
1 |
− |
t |
)‰ |
σ |
( |
t |
+ |
1 |
) − |
σ |
( |
)Ž + ( |
1 |
+ |
t |
)‰ |
σ |
( |
) − |
σ |
( |
t |
− |
1 |
)Ž |
Ì |
s t |
|
|
|
|
|
t |
|
|
|
t |
|
|
|
. |
Durch Rechteckfunktionen lassen sich beliebige Funktionen f auf genau festgelegten Intervallen [t0, t1] aktivieren. Wir sind also in Zukunft nicht mehr auf die umständliche Darstellung abschnittsweise definierter Funktionen mit geschweiften Klammern angewiesen.

14.2 Dirac-Distribution |
559 |
Satz 14.1 (Ausblendeigenschaft des Rechteckimpulses)
Durch den Rechteckimpuls |
|
|
|
|
|
|
f(t) |
|
|
|
|
||||||||||||||||||
|
r |
|
t |
) = |
σ |
( |
t |
− |
t0 |
) − |
σ |
( |
t |
− |
t1 |
) |
|
|
|
|
|
|
|
||||||
lässt |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
sich die Funktion f außerhalb des Inter- |
|
|
|
|
||||||||||||||||||||||||
|
t |
|
, t |
1] |
ausblenden: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
valls |
[ |
|
0 |
t |
t |
|
|
|
|
0 |
t |
|
für |
t0 |
|
t |
|
t0 |
|
|
f(t) r(t) |
|
|||||||
|
f |
|
|
r |
|
|
|
¢ f |
|
für |
|
t |
< |
t1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
¨ |
0 |
|
|
für |
t1 |
|
t . |
|
t |
0 |
t |
1 |
t |
|||||
|
|
( ) |
|
|
|
|
|
¨ |
|
|
( ) |
|
|
|
|
|
≤ |
|
≤ |
|
|
|
|||||||
|
|
|
( ) = ¦ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
¤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14.2 Dirac-Distribution
Distributionen sind aus mathematischer Sicht schwere Geschütze. Der Begri wurde erst im 20. Jahrhundert von dem französischen Mathematiker Laurent Schwartz geprägt. Eine mathematisch fundierte Betrachtung von Distributionen erfordert Hilfsmittel aus der Funktionalanalysis, die den Rahmen dieses Buches bei Weitem sprengen. Wir präsentieren hier einen leichter verständlichen pragmatischen Zugang und beschränken uns auf die sogenannte Dirac-Distribution, benannt nach dem Physiker Paul Adrien Maurice Dirac.
Definition 14.3 (Dirac-Distribution)
Die Rechteckfunktionen dε mit konstantem Flächeninhalt 1 erzeugen im Grenzwert für
ε gegen null die Dirac-Distribution δ.
|
|
|
|
|
1 |
|
|
|
|
|
ε → 0 |
|
|
|
|
|
|
|
|
|
|
ε |
|
dε(t) |
|
|
1 δ(t) |
|
|||||
|
|
|
|
|
|
|
ε |
|
|
|
ÐÐÐ→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
1 |
t |
|
d |
t |
) = |
1 |
‰ |
σ t |
) − |
σ |
t |
− |
ε |
)Ž |
δ t |
) = |
lim d |
t |
) |
|
ε( |
ε |
( |
( |
|
|
( |
ε→0 |
ε( |
|||||||
Ursprünglich wurde die Theorie der Distributionen in der theoretischen Physik verwendet, um Begri e wie Punktladung oder Massenpunkt mathematisch zu beschreiben. In der Physik ist für die Dirac-Distribution auch die Bezeichnung Einheitsimpuls gebräuchlich.
Der Grenzwert der Rechteckfunktion ist keine Funktion im klassischen Sinne. Trotzdem können wir uns die Dirac-Distribution als eine Art Funktion vorstellen, die an der Stelle t = 0 den Funktionswert ∞ hat und sonst überall null ist. An vielen Stellen werden wir mit der Dirac-Distribution genau wie mit einer echten Funktion rechnen. Dabei werden wir von den Eigenschaften der Dirac-Distribution aus Satz 14.2 und Satz 14.3 regen Gebrauch machen.
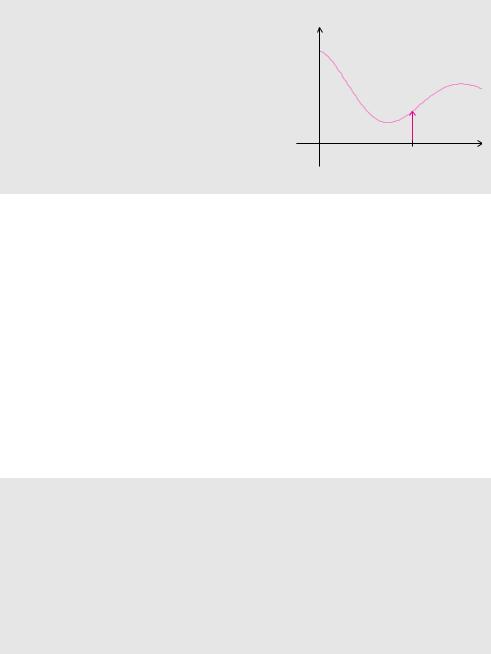
560 |
14 Verallgemeinerte Funktionen |
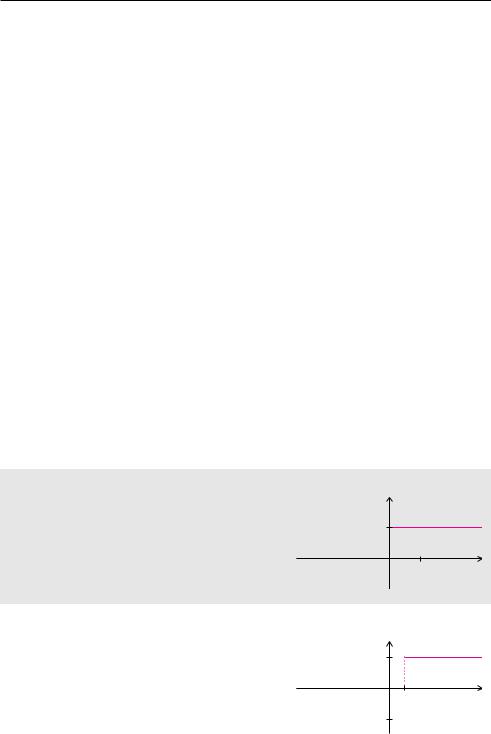
Die Dirac-Distribution besitzt eine ähnliche Ausblendeigenschaft wie der Rechteckimpuls. Allerdings findet das Ausblenden bei der Dirac-Distribution nicht über einem Intervall, sondern nur an einer einzigen Stelle t0 statt. Genau wie bei echten Funktionen verwenden wir für eine Verschiebung der Dirac-Distribution die Schreibweise δ(t − t0).
Satz 14.2 (Multiplikation mit der Dirac-Distribution)
Multipliziert man eine Funktion f mit der Dirac-Distribution δ(t − t0), dann werden alle Funktionswerte außerhalb der Stelle t0 ausgeblendet:
f(t) δ(t − t0) = f(t0) δ(t − t0).
Speziell für t0 = 0 gilt:
f(t) δ(t) = f(0) δ(t).
f(t) |
|
f(t) δ(t − t0) |
|
t0 |
t |
Bei der Definition der Dirac-Distribution sind die Rechteckfunktionen so gewählt, dass die Flächen unter den Funktionen für alle Werte von ε gleich 1 sind:
|
∞ dε |
t |
) |
dt |
= |
ε |
1 |
dt |
= |
1 |
( |
ε |
− |
0 |
) = |
1. |
|
|
|
ε |
|
||||||||||||||
S |
−∞ |
( |
|
0 ε |
|
|
|
||||||||||
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|||
Dadurch erreicht man eine Art Normierung der Dirac-Distribution. Bei der grafischen Darstellung der Dirac-Distribution δ(t − t0) verwendet man an der Stelle t = t0 einen Pfeil der Länge 1. Skalierte Dirac-Distributionen werden wir mit Pfeilen der entsprechenden Länge darstellen. Negative Skalierungsfaktoren erzeugen Pfeile mit entgegengesetzter Orientierung.
Die Integraleigenschaft bleibt im Grenzwert erhalten, auch eine Verschiebung der DiracDistribution ändert an dieser Eigenschaft nichts, deshalb gilt:
|
∞ δ t |
) |
dt |
= |
1, |
∞ δ |
t |
− |
t0 |
) |
dt |
= |
1. |
||
S |
−∞ |
( |
|
|
−∞ |
( |
|
|
|
|
|||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
Satz 14.3 (Ausblendeigenschaft der Dirac-Distribution)
Integriert man über das Produkt einer Funktion f und der Dirac-Distribution δ(t − t0), dann ergibt sich der Funktionswert an der Stelle t0:
∞
S−∞ f(t) δ(t − t0) dt = f(t0).
Insbesondere gilt für f(t) = 1 die Beziehung
∞
S−∞ δ(t − t0) dt = 1.
