11.2 Rechenregeln

Bei Problemstellungen aus der Praxis sind Berechnungen mit komplexen Zahlen Mittel zum Zweck. Ist die Darstellung oder Berechnung mit reellen Zahlen ungeschickt oder kompliziert, dann helfen oft komplexe Zahlen. Komplexe Zahlen verwendet man als Hilfsmittel, um reale Problem zu lösen. Der wesentliche Vorteil beim Rechnen mit komplexen Zahlen liegt in der Exponentialform. Berechnungen in kartesischen Koordinaten könnten wir letztendlich genau so gut mit Vektoren durchführen, siehe Abschnitt 3.3.

11.2.1 Gleichheit

Beim Vergleich von komplexen Zahlen in Exponentialform ist Vorsicht geboten. Zwei komplexe Zahlen in Exponentialform sind auch dann gleich, wenn sich ihre Winkel um ein Vielfaches von 2 π unterscheiden.

Satz 11.3 (Gleichheit komplexer Zahlen)

Zwei komplexe Zahlen z1 und z2

Lin kartesischer Form sind genau dann gleich, wenn die Realteile und die Imaginärteile übereinstimmen:

x1 + i y1 = x2 + i y2 x1 = x2 und y1 = y2.

L in Exponentialform sind genau dann gleich, wenn die Radien übereinstimmen und sich die Winkel um ein ganzzahliges Vielfaches von 2 π unterscheiden:

r1 ei ϕ1 = r2 ei ϕ2 r1 = r2 und ϕ1 = ϕ2 + 2 k π, k Z.

Komplexe Zahlen lassen sich nicht anordnen. Man kann zwar entscheiden, ob eine komplexe Zahl einen größeren Betrag oder einen größeren Winkel als eine andere komplexe Zahl hat. Auch der separate Größenvergleich von Realteilen oder Imaginärteilen ist möglich. Aber die Aussage, dass eine komplexe Zahl größer als eine andere komplexe Zahl ist, ist prinzipiell nicht definiert.

11.2.2 Addition und Subtraktion

Die Addition und Subtraktion komplexer Zahlen erfolgt koordinatenweise. Dadurch entspricht die Addition von komplexen Zahlen in kartesischer Form der Addition und Subtraktion von Vektoren, siehe Definition 3.5. Auch die Rechenregeln für Vektoren aus Satz 3.1 gelten analog für komplexe Zahlen.

Satz 11.5 (Multiplikation in kartesischer Form)

Zwei komplexe Zahlen z1 und z2 werden multipliziert, indem man die Klammern nach den üblichen Rechenregeln ausmultipliziert:

z1 z2 = (x1 + i y1) (x2 + i y2) = (x1x2 − y1y2) + i(x1y2 + y1x2).

Bei der Division mit komplexen Zahlen tritt die imaginäre Einheit i im Nenner auf. Dieses Problem lässt sich beseitigen, in dem man den Nenner mit der konjugiert komplexen Zahl erweitert.

Satz 11.6 (Division in kartesischer Form)

Zwei komplexe Zahlen z1 und z2 werden dividiert, indem man den Nenner durch konjugiert komplexes Erweitern reell macht:

Beispiel 11.4 (Multiplikation und Division komplexer Zahlen in kartesischer Form)

a) Das Produkt der beiden komplexen Zahlen −3 + 2 i und 2 − i ergibt

(−3 + 2 i) (2 − i) = −6 + 3 i + 4 i − 2 i2 = −6 + 7 i + 2 = −4 + 7 i.

b) Die Division der Zahl 2 + i durch die komplexe Zahl 1 − i erfolgt durch Erweitern mit 1 + i:

Zur Multiplikation und Division komplexer Zahlen in Exponentialform verwenden wir die Potenzgesetze aus Satz 1.4. Diese Rechenregeln behalten auch für imaginäre Hochzahlen ihre Gültigkeit.

Satz 11.7 (Multiplikation und Division in Exponentialform)

Zwei komplexe Zahlen z1 und z2 werden

L multipliziert, indem man die Beträge multipliziert und die Argumente addiert:

z1 z2 = r1 ei ϕ1 r2 ei ϕ2 = (r1 r2) ei (ϕ1+ϕ2),

L dividiert, indem man die Beträge dividiert und die Argumente subtrahiert:

Die Rechenregeln für Beträge reeller Zahlen lassen sich auf komplexe Zahlen übertragen. Formeln für das Produkt und den Quotienten komplexer Zahlen ergeben sich am einfachsten in Exponentialform. Für das Produkt zweier komplexen Zahlen z1 und z2 gilt:

Sz1 z2S = Tr1 ei ϕ1 r2 ei ϕ2 T = r1 r2 Tei ϕ1 T Tei ϕ2 T = Sz1S Sz1S .

² ²

11

Eine Formel für den Quotienten zweier komplexer Zahlen lässt sich analog herleiten.

Satz 11.9 (Rechenregeln für den Betrag komplexer Zahlen)

Für komplexe Zahlen z1 und z2 gelten folgende Rechenregeln für den Betrag:

Der Betrag komplexer Zahlen hat eine anschauliche Bedeutung in der komplexen Ebene. Er entspricht dem Abstand zum Ursprung. Somit gibt der Betrag der Di erenz zweier komplexer Zahlen den Abstand dieser beiden Zahlen an.

»

Sz1 − z2S = (x1 − x2)2 + (y1 − y2)2.

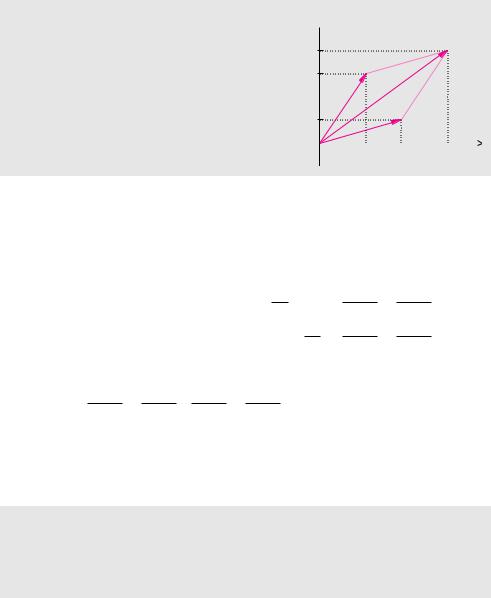
Bei komplexen Zahlen bekommt der Begri Dreiecksungleichung, den wir für reelle Zahlen bereits aus Satz 1.3 kennen, eine anschauliche Bedeutung. Das Dreieck wird aus den Zahlen z1, z2 und z1 + z2 in der komplexen Ebene gebildet. Die erste Dreiecksungleichung besagt anschaulich, dass die Länge der Hypotenuse nicht länger als die Summe der Längen der beiden Katheten ist. Anschaulich bedeutet die zweite Dreiecksungleichung, dass die Länge der Diagonale in einem Parallelogramm immer größer ist als die Di erenz der Längen der beiden Seiten.

Satz 11.10 (Dreiecksungleichungen für den Betrag komplexer Zahlen)

L Sz1 ± z2S ≥ U Sz1S − Sz2S U

z1

Re