
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
442 |
11 Komplexe Zahlen und Funktionen |
Beispiel 11.9 (Zerlegung in komplexe Linearfaktoren)
a) Wir suchen alle Lösungen der Gleichung
z3 + z2 + 8 z − 10 = 0.
Eine Lösung ist z1 = 1. Dadurch kann man den Linearfaktor z − 1 abspalten:
‰ |
|
z3 |
z2 |
+ 8 |
z |
− 10 Ž ‰ |
z |
z2 |
+ 2 |
z |
+ 10 |
− |
z3 |
+ z2 |
|
− 1Ž = |
|
|
|||||
|
|
+ |
|
|
|
|
|
|
|
|
2z2 + 8z
− 2z2 + 2z
10z − 10 − 10z + 10
0
Die beiden restlichen Lösungen bilden ein konjugiert komplexes Paar:
|
2 |
|
i√ |
|
|
|
− |
± |
40 |
− |
4 |
||
|
2 |
|
|
b)Wir suchen eine Gleichung, die die komplexe Lösung z1 = −1 + i hat. Damit die Koe zienten der Gleichung alle reell sind, muss auch die konjugiert komplexe Zahl z2 = −1 − i eine Lösung sein. Dadurch ergibt sich die Darstellung mit Linearfaktoren:
‰ |
z |
− (− |
1 |
i z |
− (− |
1 |
i |
z |
+ |
1 |
− |
i |
)( |
z |
+ |
1 |
+ |
i |
) = ( |
z |
+ |
1 |
) |
2 |
− |
i2 |
= |
z2 |
+ |
2 z |
+ |
2. |
|
|
+ )Ž‰ |
|
− )Ž = ( |
|
|
® |
|
|
® |
|
|
|
¯ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
± |
|
|
± |
|
´¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
a |
|
|
b |
|
|
a2 |
|
|
|
b2 |
|
|
|
|
|
|
|
Die gesuchte Gleichung lautet z2 + 2 z + 2 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
||||||||||||||
11.4 Komplexe Funktionen
Die Untersuchung komplexer Funktionen ist im Rahmen der sogenannten Funktionentheorie ein großes Gebiet der Mathematik mit entsprechend weitreichendem Anwendungsspektrum. Wesentlich beeinflusst haben die Funktionentheorie Mathematiker wie AugustinLouis Cauchy, Karl Theodor Wilhelm Weierstraß, Felix Klein und Félix Édouard Justin Émile Borel. Im Grunde lassen sich mit komplexen Zahlen genau wie mit reellen Zahlen Funktionen definieren. Eine komplexwertige Funktion mit einer komplexen Variablen ist eine Abbildung, die jeder komplexen Zahl aus dem Definitionsbereich eine komplexe Zahl zuordnet. Bereits die grafische Darstellung von komplexen Funktionen stellt eine Herausforderung dar. Komplexwertige Funktionen von komplexen Veränderlichen erfordern die Visualisierung von vier Dimensionen. Wir betrachten deshalb in diesem Abschnitt nur einfache komplexwertige Funktionen. Das sind zum einen Funktionen, die einer reellen Zahl eine komplexe Zahl zuordnen, und zum anderen Transformationen der komplexen Ebene, wie etwa Verschiebungen, Skalierungen und Rotationen. Außerdem verwenden wir die Darstellung harmonischer Schwingungen mithilfe komplexer Zeiger zur Überlagerung gleichfrequenter harmonischer Schwingungen.
11.4 Komplexe Funktionen |
443 |
11.4.1 Ortskurven
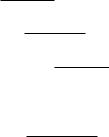
Insbesondere in der Elektrotechnik betrachtet man komplexe Größen, die von reellen Parametern abhängen. Eine Kurve, die durch komplexe Zahlen in der Gaußschen Zahlenebene beschrieben wird, nennt man Ortskurve. Durchläuft der Parameter ein Intervall der reellen Zahlen, so ergibt sich für jeden Parameter eine komplexe Zahl.
Definition 11.9 (Komplexwertige Funktion einer reellen Variablen, Ortskurve)
Bei einer komplexwertigen Funktion einer reellen Variablen hängen die komplexen Zahlen z von einem reellen Parameter t im Intervall I ab:
z = z(t), t I.
Die zugehörige Bahnkurve aller komplexen Zahlen z in der Gaußschen Zahlenebene nennt man
Ortskurve.
Im |
) |
t |
( |
z |
Re |
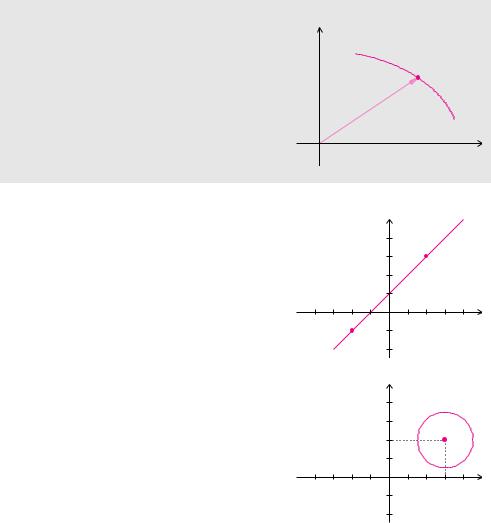
Beispiel 11.10 (Ortskurven)
a) Die komplexwertige Funktion
z(t) = (1 − t)(−2 − i) + t(2 + 3 i), t R
besitzt als Ortskurve eine Gerade in der komplexen Ebene durch die beiden Zahlen z(0) = −2 − i und z(1) = 2 + 3 i. Man kann die Funktion durch
z(t) = −2 − i + 4 t(1 + i), t R
darstellen.
b) Die Ortskurve der komplexwertigen Funktion
z(t) = 3 + 2 i + |
3 |
e |
i t |
, t [0, 2 |
π] |
2 |
|
ist ein Kreis mit Mittelpunkt z0 = 3 + 2 i und Radius r = 32 . Das kann man überprüfen durch
Sz(t) − z0S = V |
3 |
e |
i t |
V = |
3 |
Te |
i t |
T = |
3 |
||
|
|
|
|
|
|
. |
|||||
2 |
|
2 |
|
2 |
|||||||
Im |
|
|
4i |
|
|
3i |
z(1) |
|
|
||
2i |
|
|
i |
|
|
−4 −3 −2 −1 |
1 2 3 4 Re |
|
z(0)−i |
|
|
−2 i |
|
|
Im |
|
|
4i |
|
|
3i |
z0 |
|
2i |
||
|
||
i |
|
|
−4 −3 −2 −1 |
1 2 3 4 Re |
|
−i |
|
|
−2 i |
|

444 |
11 Komplexe Zahlen und Funktionen |
c) Bei der Ortskurve der komplexwertigen Funktion
4
z(t) = , t R
1 + 4 i t
erkennt man den Kurventyp nicht auf den ersten Blick. Man kann jedoch zeigen, dass gilt:
Sz(t) − 2S = 2.
Die Ortskurve ist also ein Kreis mit Mittelpunkt bei z0 = 2 und Radius 2.
Im 
4i
3i
2i
i z(−1)
z0 z(0)
−4 −3 −2 −1 |
1 2 3 4 Re |
−i  z(1)
z(1)
−2 i
Ì
Ortskurven lassen sich in kartesischer Form oder in Exponentialform darstellen:
z(t) = x(t) + i y(t) = r(t) ei ϕ(t), t I.
Die kartesische Form entspricht der Parameterdarstellung ebener Kurven, siehe Definition 9.1. Die Darstellung in Exponentialform entspricht der Darstellung ebener Kurven in Polarkoordinaten, siehe Definition 9.2.
11.4.2 Harmonische Schwingungen
Die mathematische Beschreibung von Schwingungsvorgängen ist Bestandteil vieler Problemstellungen in Naturwissenschaft und Technik. Unter einer harmonischen Schwingung versteht man eine Oszillation, die sich in Form einer Sinusoder Kosinusfunktion darstellen lässt, siehe Definition 5.28. Technische Vorgänge lassen sich nur bei idealisierten Annahmen durch reine harmonische Schwingungen beschreiben. Trotzdem bilden harmonische Schwingungen die Grundlage jeder Schwingungsanalyse. Dabei betrachtet man harmonische Schwingungen meistens nicht in Form von Sinusoder Kosinusfunktionen, sondern in Form komplexer Funktionen mit einer reellen Veränderlichen, siehe Kapitel 13 und Kapitel 12.
Satz 11.17 (Harmonische Schwingung)
Jede harmonische Schwingung mit Kreisfrequenz ω lässt sich sowohl durch eine Amplitude A > 0 und einen Phasenwinkel ϕ mit dem Kosinus als Grundfunktion als auch durch Überlagerung phasenwinkelfreier Sinusund Kosinusfunktionen darstellen:
A cos (ω t + ϕ) = C1 cos (ω t) + C2 sin (ω t).
Zur Umrechnung zwischen den beiden Darstellungen gelten die Formeln:
»
L A = C12 + C22
L ϕ = arg(C1 − i C2)
11.4 Komplexe Funktionen |
445 |
Die Formeln aus Satz 11.17 kann man mit den Darstellungen von Sinus und Kosinus durch komplexe e-Funktionen aus Satz 11.2 herleiten:
A ei (ω t+ϕ) |
e−i (ω t+ϕ) |
|
C1 |
ei ω t |
|
e−i ω t |
C2 |
ei ω t |
|
e−i ω t . |
|
+2 |
= |
|
|
+2 |
+ |
|
|
− |
|
|
|
|
|
|
|
|
|
|
2 i |
|
Daraus ergibt sich
ei ω t |
A ei ϕ |
C1 |
i C2 |
Ž + |
e−i ω t |
A e−i ϕ |
C1 |
i C2 |
Ž = |
0. |
|
‰ A ei ϕ |
− C1 |
+ i C2 |
|
‰ A e−i ϕ |
− C1 |
− i C2 |
|
||
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|
||||
|
|
= |
− |
|
|
|
= |
+ |
|
|
Die Gleichung ist sicher erfüllt, wenn A ei ϕ = C1 − i C2. Die Darstellung in Satz 11.17 verwendet den Kosinus als Grundfunktion. Genau so gut könnten wir auch den Sinus verwenden. Mit C1 = 0 und C2 = 1 ergibt sich
A = 1, ϕ = arg(−i) = − |
π |
Ô sin (ω t) = cos ‹ω t − |
π |
•. |
2 |
2 |
Man sagt, der Kosinus eilt dem Sinus um den Phasenwinkel π2 voraus.
Beispiel 11.11 (Harmonische Schwingungen) |
|
|
|
|
|
|
|
|
|
||||||||||||
a) |
Die harmonische Schwingung |
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
x |
t |
) = − |
cos t |
+ |
sin t |
|
|
|
1 |
|
|
cos t |
|
|
|
|
||||
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
können wir durch |
|
|
|
|
|
|
|
− |
−cos t + sin t |
|||||||||||
|
A = √2, ϕ = arg(−1 − i) = − |
34 |
|
−1 |
sin t |
|
2π |
|
|
|
t |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
π |
|
|
|
|
|
|
|
|
auch als phasenverschobenen Kosinus darstellen: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
x(t) = √2 cos ‹t − |
34 |
•. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
b) |
Aus der Darstellung |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
2 cos |
t |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
|
x(t) = 2 cos |
|
|
|
• |
|
|
|
|
|
|
|
¡ |
|
− |
¢ |
|||||
|
‹t − 3 |
|
|
|
1 |
|
cos t |
|
|
||||||||||||
|
ergibt sich mit |
|
|
|
|
|
|
|
3 • = √3 |
|
|
|
|
|
|
|
|
|
|||
|
C1 = 2 cos ‹ |
3 |
• = 1, |
C2 = 2 sin ‹ |
− |
π |
|
|
2π |
|
|
|
t |
||||||||
|
|
|
|
√3 sin t |
|
|
|||||||||||||||
|
|
|
|
|
π |
|
|
|
|
|
π |
1 |
|
|
|
|
|
|
|
|
|
|
die phasenwinkelfreie Darstellung |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x(t) = cos t + √3 sin t. |
|
|
|
|
|
|
|
|
|
|
Ì |
|||||||||
446 |
11 Komplexe Zahlen und Funktionen |
Sinus und Kosinus sind am Einheitskreis definiert, siehe Definition 5.25. Wir übertragen diese Definition nun auf die Gaußsche Zahlenebene. Zu einer harmonischen Schwingung x betrachten wir eine komplexwertige Funktion z, die von einem reellen Parameter abhängt:
x(t) = A cos (ω t + ϕ) Ð→ z(t) = A cos (ω t + ϕ) + i A sin (ω t + ϕ).
Die Ortskurve der Funktion z beschreibt einen Ursprungskreis mit Radius A in der komplexen Ebene. Man nennt z eine komplexe Ersatzgröße für x. Diese Vorgehensweise erweckt den Eindruck, dass man aus einer einfachen reellen Funktion x eine komplizierte komplexe Funktion z erzeugt hat. Das Gegenteil ist der Fall. Nach dem Satz von Euler, Satz 11.1, gilt:
z(t) = A cos (ω t + ϕ) + i A sin (ω t + ϕ) = A ei (ω t+ϕ).
Wir werden sehen, dass sich in der Darstellung mit der e-Funktion viele Berechnungen einfacher durchführen lassen als in der ursprünglichen reellen Form mit dem Kosinus.
Definition 11.10 (Zeiger einer harmonischen Schwingung)
Einer harmonischen Schwingung kann man eine
Schwingung im Komplexen zuordnen:
A cos (ω t + ϕ) Ð→ A ei (ω t+ϕ)
Bei dieser Zeigerdarstellung nennt man
z0 = A ei ϕ
den Zeiger der harmonischen Schwingung.
Im 
z |
|
i ϕ |
0 |
= A e |
|
|
|
|
A |
|
|
ϕ |
|
|
A cos ϕ |
Re |
|
Wenn der Parameter t die reellen Zahlen durchläuft, dann durchläuft die Ortskurve der Schwingung im Komplexen z den Kreis unendlich oft. Der Zeiger z0 ist aber eine feste komplexe Zahl
z0 = z(0) = A ei (ω 0+ϕ) = A ei ϕ.
Er gibt den Phasenwinkel zum Parameterwert t = 0 an. Deshalb bezeichnet man ϕ auch als Nullphasenwinkel. Durch komplexe Zeiger lässt sich die Überlagerung harmonischer Schwingungen elegant berechnen. Nach Satz 11.17 lässt sich jede harmonische Schwingung mit Kosinus als Grundfunktion darstellen. Somit betrachten wir zwei harmonische Schwingungen x1 und x2 in der Form
x1(t) = A1 cos (ω t + ϕ1), x2(t) = A2 cos (ω t + ϕ1).
Dabei setzen wir voraus, dass beide Schwingungen dieselbe Kreisfrequenz ω besitzen. Anstatt der Überlagerung der reellen Funktionen x1 und x2 betrachten wir die Addition der Schwingungen im Komplexen z1 und z2:
x1(t) + x2(t) Ð→ z1(t) + z2(t) = A1 ei (ω t+ϕ1) + A2 ei (ω t+ϕ2) = A ei (ω t+ϕ).
11.4 Komplexe Funktionen |
447 |
Unser Ziel ist es, A und ϕ in Abhängigkeit von A1, A2, ϕ1 und ϕ2 darzustellen. Aufgrund der gemeinsamen Kreisfrequenz lässt sich die Gleichung durch ei ω t teilen:
A1 ei (ω t+ϕ1) + A2 ei (ω t+ϕ2) = A ei (ω t+ϕ) Ô A1 ei ϕ1 + A2 ei ϕ2 = A ei ϕ.
Diese Gleichung stellt eine gewaltige Vereinfachung dar. Sie ist unabhängig vom Parameter t. Unsere gesuchten Größen A und ϕ lassen sich durch Addition der Zeiger ermitteln.
Überlagerung harmonischer Schwingungen durch Zeigeraddition
Die Überlagerung x der beiden harmonischen Schwingungen x1 und x2 mit gleicher Kreisfrequenz ω kann folgendermaßen durchgeführt werden:
(1) Stelle beide harmonischen Schwingungen als phasenverschobenen Kosinus dar:
x1(t) = A1 cos (ω t + ϕ1), x2(t) = A2 cos (ω t + ϕ2).
(2) Ordne jeder Schwingung den entsprechenden komplexen Zeiger zu:
x1(t) Ð→ z1 = A1 ei ϕ1 , |
x2(t) Ð→ z2 = A2 ei ϕ2 . |
(3)Stelle die Addition der beiden Zeiger in Exponentialform dar: z = z1 + z2 = A1 ei ϕ1 + A2 ei ϕ2 = A ei ϕ.
(4)Die überlagerte Schwingung x hat die Amplitude A und den Phasenwinkel ϕ: x(t) = x1(t) + x2(t) = A cos (ω t + ϕ).
Die Überlagerung harmonischer Schwingungen durch Zeigeraddition erfordert die Addition zweier komplexer Zahlen in Exponentialform. Dazu müssen die beiden Zahlen zunächst in kartesische Form umgerechnet werden. Dann addiert man die beiden Realteile und die beiden Imaginärteile. Schließlich wird das Ergebnis in Exponentialform umgerechnet.
Beispiel 11.12 (Überlagerung harmonischer Schwingungen durch Zeigeraddition)
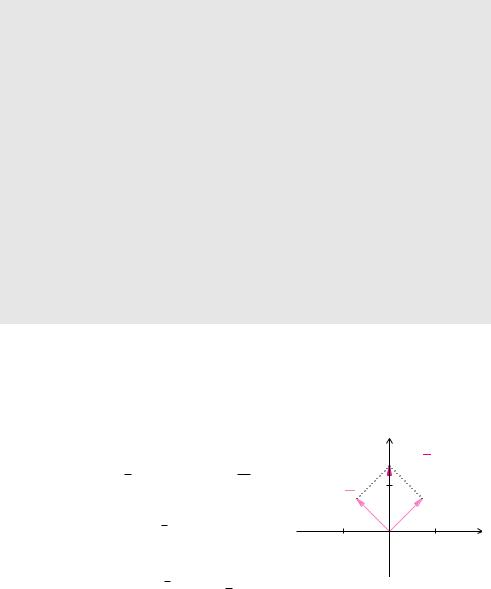
a) |
Zur Addition der harmonischen Schwingungen |
|
Im |
√ |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
i π2 |
|
|
|
|
|
)= |
cos |
‹ |
2t |
π |
|
|
)= |
cos |
‹ |
2t |
|
3π |
|
|
2e |
|
|||
|
x1 |
t |
, x2 |
t |
|
z2 = ei 34π |
i |
z1 = ei π4 |
|
|||||||||||||
|
|
( |
|
|
|
+ • |
|
( |
|
|
+ • |
|
||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
addieren wir die beiden Zeiger |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
z1 |
|
z2 |
ei π4 |
|
ei 34π |
√2ei π2 . |
|
|
|
|
−1 |
|
|
1 |
Re |
||||||
|
Dadurch+ |
ergibt= |
sich+ |
= |
|
|
|
|
|
|
•. |
|
|
|
|
|
||||||
|
x(t) = x1(t) + x2(t) = √2 cos ‹2 t + |
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
