
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

204 |
5 Funktionen |
Die Bezeichnung mit dem „großen O“ geht auf die beiden deutschen Mathematiker Paul Bachmann und Edmund Landau zurück. Manchmal wird auch die Bezeichnung mit dem Gleichheitszeichen ak = O(bk) anstelle der Elementrelation verwendet. Streng genommen ist diese Bezeichnung nicht korrekt, denn viele unterschiedliche Folgen können dieselbe asymptotische obere Schranke besitzen, siehe Beispiel 5.52.
Das Landau-Symbol wird in der theoretischen Informatik bei der Komplexitätsanalyse von Algorithmen verwendet. Es gibt auch noch ein Landau-Symbol mit dem „kleinen o“. Auf weitere Details dazu verzichten wir und verweisen auf [Heuser:Analysis] und [Höllig].
5.5.2 Grenzwert einer Funktion
An den Stellen, an denen eine Funktion eine Definitionslücke besitzt, kann man keinen Funktionswert berechnen. Mithilfe von Folgen können wir uns jedoch beliebig nahe an Definitionslücken herantasten. Bei diesem Herantasten an eine Definitionslücke entstehen unterschiedliche E ekte, die wir genauer analysieren werden.
Beispiel 5.53 (Grenzwert einer Funktion)
Die |
Funktion |
1 |
|
x3 cos |
2 x |
|
ist |
|
|
x |
|
0 |
|
|
|
|
anderen |
|||||||
f x |
− |
−x2 |
( |
) |
|
|
|
|
|
|
|
|
||||||||||||
-Werten |
|
( ) = |
|
|
|
zwar für |
|
= |
|
nicht |
definiert, zu allen |
1 |
|
|||||||||||
x |
|
|
können wir die Funktionswerte jedoch berechnen. Die Folge mit den Gliedern ak |
|
|
|
||||||||||||||||||
|
|
|
10k |
|||||||||||||||||||||
konvergiert gegen die Definitionslücke |
x |
|
0 |
. Wenn wir die Folgenglieder in die Funktion |
einsetzen, |
|||||||||||||||||||
|
= |
|
|
= − |
||||||||||||||||||||
erhalten wir |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ak |
|
−0.1000 |
−0.0100 |
−0.0010 |
−0.0001 |
|
. . . |
→ |
0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
f(ak) |
|
2.0933 |
2.0099 |
2.0010 |
2.0001 |
|
. . . |
→ |
2? |
|
|
|
|
|
||||||||
1
Auch die Folge mit den Gliedern bk = 10k konvergiert gegen die Definitionslücke x = 0. Eingesetzt in die Funktionsgleichung ergibt sich
|
bk |
−0.1000 |
−0.0100 |
−0.0010 |
−0.0001 |
. . . → 0 |
|
|
|
|
||||
|
f(bk) |
1.8933 |
|
1.9899 |
1.9990 |
1.9999 |
. . . → 2? |
|
|
|||||
Alle Folgenglieder der Folge |
ak |
sind negativ, sie nähern sich der Definitionslücke x 0 von |
||||||||||||
links. Entsprechend nähert |
sich die Folge |
bk |
der Definitionslücke x 0 von rechts. Aufgrund |
|||||||||||
|
( ) |
|
|
|
|
|
|
|
= |
|
||||
der Zahlenwerte vermuten wir, dass die |
Funktionswerte in beiden Fällen gegen den Grenzwert 2 |
|||||||||||||
|
( ) |
|
|
= |
|
Ì |
||||||||
konvergieren. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Die Vorgehensweise in Beispiel 5.53 zur Ermittlung des Grenzwerts einer Funktion ist zwar mithilfe von Taschenrechnern oder Computern einfach möglich. Aus Sicht der Mathematik ist diese intuitive Methode jedoch unbefriedigend. Wir werden später eine Methode zur Grenzwertbestimmung kennenlernen, die unter dem Namen Bernoulli-de l’Hospital bekannt ist, siehe Abschnitt 6.3.

5.5 Grenzwert und Stetigkeit |
205 |
Definition 5.38 (Grenzwert einer Funktion)
Die Funktion f hat an der Stelle x0 den Grenzwert G, wenn für jede gegen x0 konvergente Zahlenfolge (xn) die Folge der Funktionswerte (f(xn)) gegen G konvergiert.
Man verwendet die Schreibweise f(x) → G für x → x0 oder lim f(x) = G.
x→x0
Diese Definition ist für praktische Zwecke ungeeignet, denn sie fordert, dass man alle gegen x0 konvergenten Zahlenfolgen betrachtet. Ähnlich wie bei der Definition des Grenzwert einer Zahlenfolge, siehe Definition 5.33, kann man den Grenzwert einer Funktion auch mithilfe einer ε-Umgebung definieren. Für Grenzwerte von Funktionen gelten entsprechende Rechenregeln wie für Grenzwerte von Zahlenfolgen, siehe Satz 5.15.
Satz 5.17 (Rechnen mit Funktionsgrenzwerten)
|
f |
|
g |
lim f |
x |
F |
lim g |
x |
G |
|
Wenn |
|
und |
|
Funktionen sind mit x→x0 |
( ) = |
|
und x→x0 |
( ) = |
|
, dann gilt: |
L Es existiert auch der Funktionsgrenzwert von f(x) ± g(x) an der Stelle x0, nämlich
lim (f(x) ± g(x)) = F ± G.
x→x0
L Es existiert auch der Funktionsgrenzwert von f(x) g(x) an der Stelle x0, nämlich
lim (f(x) g(x)) = F G.
x→x0
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|
|
L |
Es existiert auch der Funktionsgrenzwert |
von |
g(x) |
an |
der Stelle x0, nämlich |
||||||||||
lim |
f x |
|
F |
|
Funktion g x |
|
in einer Umgebung von |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
g |
(x) |
|
G |
. Das gilt nur, wenn die |
|
|||||||||
|
x |
→ |
x0 |
|
|
|
( ) |
( |
) |
|
|||||
|
|
|
Π|
( ) |
‘ = |
|
|
|
|
||||||
x0 und der Grenzwert G nicht null sind.
Nicht immer liefert die Annäherung von links und die Annäherung von rechts dasselbe Ergebnis. Deshalb unterscheidet man zwischen linksseitigem und rechtsseitigem Grenzwert.
Definition 5.39 (Linksseitiger und rechtsseitiger Grenzwert)
Wenn man bei der Grenzwertberechnung einer Funktion f an der Stelle x0 nur Zahlenfolgen (xn) betrachtet, die kleinere Werte als x0 enthalten, dann bezeichnet man den Grenzwert als linksseitigen Grenzwert GL, Zahlenfolgen mit größeren Werten als x0 erzeugen den rechtsseitigen Grenzwert GR. Man verwendet die Schreibweisen
lim |
− |
f |
( |
x |
) = |
G |
L |
, |
lim |
+ |
f |
x |
G |
R |
. |
x→x0 |
|
|
|
|
x→x0 |
|
( ) = |
|
|
206 |
5 Funktionen |
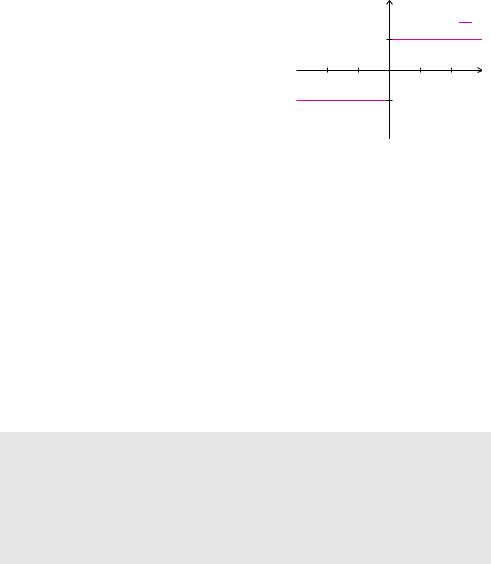
Beispiel 5.54 (Linksund rechtsseitige Grenzwerte)
Die Funktion f x |
|
x |
|
hat eine Definitionslücke bei |
||||||||||||||
|
x |
|
||||||||||||||||
|
|
|
. Eine |
|
|
|
|
S |
|
|
|
|
|
|
|
|||
x |
= |
0 |
|
( ) = S |
|
|
|
|
|
|
|
|||||||
|
|
Folge, die von links gegen 0 konvergiert, |
||||||||||||||||
hat nur negative Glieder. Folglich ist |
||||||||||||||||||
|
|
|
GL |
= |
lim f |
x |
|
|
lim |
x |
|
|
1. |
|||||
|
|
|
|
|
− |
|
|
|||||||||||
|
|
|
|
|
x 0 |
|
( ) = |
x 0 |
|
|
= − |
|||||||
Andererseits hat→ |
−eine Folge,→ |
−diexvon rechts gegen 0 |
||||||||||||||||
konvergiert, nur positive Glieder. Somit gilt |
||||||||||||||||||
|
|
|
G |
R |
|
lim f |
x |
|
|
lim |
x |
= |
1. |
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
= x→0+ |
( ) = x→0+ x |
|
||||||||||||
|
|
y |
|
|
|
|
f (x) = |
x |
|
|
|
1 |
|
|x| |
|
|
|
|
|
−2 |
−1 |
1 |
2 |
x |
|
||||
|
|
−1 |
|
|
|
|
|
|
Ì |
5.5.3 Stetigkeit
Anschaulich versteht man unter einer stetigen Funktion eine Funktion, deren Schaubild keine Sprungstellen hat. Demnach kann das Schaubild einer stetigen Funktion ohne Absetzen des Stiftes gezeichnet werden. Der Begri der Stetigkeit ist jedoch von so zentraler Bedeutung, dass wir uns nicht mit einer anschaulichen Beschreibung begnügen wollen.
Die ursprüngliche Definition der Stetigkeit geht auf die Mathematiker Augustin-Louis Cauchy und Bernhard Placius Johann Nepomuk Bolzano zurück. Sie bezeichneten eine Funktion als stetig, wenn kleine Änderungen im Argument der Funktion nur kleine Änderungen im Funktionswert bewirken. Basierend auf dieser Idee hat der deutsche Mathematiker Karl Weierstraß das sogenannte ε-δ-Kriterium zur Beurteilung der Stetigkeit eingeführt. Danach ist eine Funktion genau dann stetig, wenn zu jedem ε > 0 ein δ > 0 existiert, sodass für alle x mit Sx − x0S < δ die Abschätzung Sf(x) − f(x0)S < ε gilt. Alternativ dazu kann man Stetigkeit auch mithilfe von Grenzwerten von Funktionen definieren.
Definition 5.40 (Stetigkeit)
Eine Funktion f heißt stetig an der Stelle x0, wenn der Grenzwert der Funktion für x gegen x0 existiert und gleich dem Funktionswert an der Stelle x0 ist, falls also gilt:
lim f(x) = f(x0).
x→x0
Man nennt eine Funktion stetig auf einem Intervall, wenn sie an allen Stellen des Intervalls stetig ist.
Fasst man x0 als Grenzwert auf, also x0 = lim x, so lautet die Definition der Stetigkeit
x→x0
lim f(x) = f ‹ lim x• .
x→x0 x→x0
Diese scheinbar umständliche Schreibweise erlaubt jedoch eine andere Interpretation der Stetigkeit. Stetigkeit bedeutet demnach, dass man Grenzwertberechnung und Funktionsberechnung vertauschen darf. Diese Erlaubnis zum Vertauschen ist eine zentrale und wichtige Eigenschaft stetiger Funktionen. Deshalb sei dies hier nochmals ausdrücklich betont.

5.5 Grenzwert und Stetigkeit |
207 |
Bedingungen für Stetigkeit
Eine Funktion ist genau dann stetig an der Stelle x0, wenn alle folgenden Bedingungen erfüllt sind:
(1)Die Funktion ist an der Stelle x0 selbst und in einer Umgebung der Stelle x0 definiert.
(2)Der Grenzwert der Funktion an der Stelle x0 existiert. Insbesondere müssen der linksseitige Grenzwert GL und der rechtsseitige Grenzwert GR an der Stelle x0 existieren und gleich sein.
(3)Grenzwert und Funktionswert stimmen an der Stelle x0 überein.
Beispiel 5.55 (Untersuchung auf Stetigkeit)
a) |
Die Funktion f x |
|
|
1 |
|
ist an der Stelle x 1 nicht definiert, also erst recht nicht stetig. |
|||||||
|
x |
− |
1 |
||||||||||
|
|
|
|
|
|
stimmen linksseitiger und rechtsseitiger Grenzwert an der |
|||||||
b) |
Bei der |
Funktion f x |
sgn x |
|
|||||||||
( ) = |
|
|
|
|
|
|
= |
|
|
||||
|
Stelle 0 nicht überein, denn GL |
|
lim sgn x |
|
1 und GR lim sgn x 1. Somit ist die |
||||||||
|
|
|
( |
) = |
|
( ) |
x 0 |
|
|
x 0 |
|
||
|
Funktion an der Stelle x |
|
0 auch nicht stetig. |
= → + ( ) = |
|
||||||||
|
|
|
|
|
|
= |
|
= |
→ − |
( ) = − |
Ì |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Abgesehen von ihren Definitionslücken sind alle elementaren Funktionen überall stetig.
Stetigkeit elementarer Funktionen
Alle elementaren Funktionen sind auf ihrem Definitionsbereich überall stetig.
Die Summe, die Di erenz, das Produkt und der Quotient stetiger Funktionen ergibt wieder eine stetige Funktion.
Satz 5.18 (Kombination stetiger Funktionen)
Wenn f und g stetige Funktionen an der Stelle x0 sind, dann gilt:
L |
Die Funktion f ± g ist auch stetig in x0. |
||
L |
Die Funktion f g ist auch stetig in x0. |
||
L |
f |
||
Die Funktion |
|
ist auch stetig in x0, falls g(x0) ≠ 0. |
|
g |
|||
Auch für die Komposition von stetigen Funktionen gilt, dass das Resultat wieder eine stetige Funktion ergibt.
Satz 5.19 (Komposition stetiger Funktionen)
Wenn g eine stetige Funktion an der Stelle x0 ist und f eine stetige Funktionen an der Stelle f(x0) ist, dann gilt: Die Funktion f ○ g ist auch stetig an der Stelle x0.

208 |
5 Funktionen |
Unstetigkeitsstellen von Funktionen entstehen vor allem durch Definitionslücken. Je nachdem, welchen linksseitigen und rechtsseitigen Grenzwert die Funktion an einer Definitionslücke besitzt, unterscheidet man hebbare Definitionslücken, Sprungstellen und Polstellen.
Unstetigkeitsstellen
Man unterscheidet folgende Arten von Unstetigkeitsstellen:
LHebbare Unstetigkeitsstelle,
LUnstetigkeitsstelle 1. Art oder Sprungstelle,
LUnstetigkeitsstelle 2. Art, etwa eine Polstelle oder eine Oszillationsstelle.
Betrachten wir zunächst den harmlosesten Fall der Unstetigkeit. An einer hebbaren Unstetigkeitsstelle ist die Funktion im Grund nur falsch definiert.
Definition 5.41 (Hebbare Unstetigkeitsstelle)
Wenn bei einer Funktion f der linksseitige Grenzwert GL = lim f(x) und der rechts-
x→x0−
|
G |
lim |
+ |
f |
( |
x |
) |
|
x |
|
seitige Grenzwert |
|
R = x→x0 |
|
|
an der Stelle |
0 |
existieren und gleich sind, also |
GL = G = GR, aber nicht mit Funktionswert f(x0) übereinstimmen oder die Funktion f an der Stelle x0 nicht definiert ist, dann kann man durch
f˜ x |
¢ |
f |
G |
|
für x |
|
x0 |
, |
|
¨ |
|
( |
) |
|
≠ |
|
|
( |
¨ |
|
|
|
|
|
|
|
) = ¦ |
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
= |
|
|
|
¨ |
|
|
|
|
|
|
|
|
¤ |
|
|
|
|
|
|
|
eine neue Funktion definieren, die an der Stelle x0 stetig ist. Die Stelle x0 heißt hebbare Unstetigkeitsstelle.
Beispiel 5.56 (Hebbare Unstetigkeitsstelle) |
|
||||
Bei der Funktion f x |
1 x3 |
cos 2 x |
aus Beispiel 5.53 hat der linksseitige und der rechts- |
||
|
x2 |
||||
|
der Funktion− |
x 0 den Wert 2. Die neue Funktion |
|||
seitige Grenzwert |
( ) = |
|
|
= |
|
|
|
|
|
|
|
f˜ x |
¢ 1 |
x3 |
x2 |
|
2 x |
||
|
¨ − |
|
− |
|
( |
) |
|
|
¨ |
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
( |
¨ |
|
|
|
2 |
|
|
) = ¦ |
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
¤ |
|
|
|
|
|
|
für x ≠ 0
für x = 0
ist für alle reellen Zahlen definiert und stetig. |
Ì |
Definition 5.42 (Sprungstelle)
Wenn bei einer Funktion f der linksseitige Grenzwert GL = lim f(x) und der rechts-
x→x0−
seitige Grenzwert GR = lim f(x) an der Stelle x0 existieren, aber nicht gleich sind,
x→x0+
also GL ≠ GR, dann bezeichnet man diese Unstetigkeitsstelle als Sprungstelle oder
Unstetigkeitsstelle 1. Art.
5.5 Grenzwert und Stetigkeit |
209 |
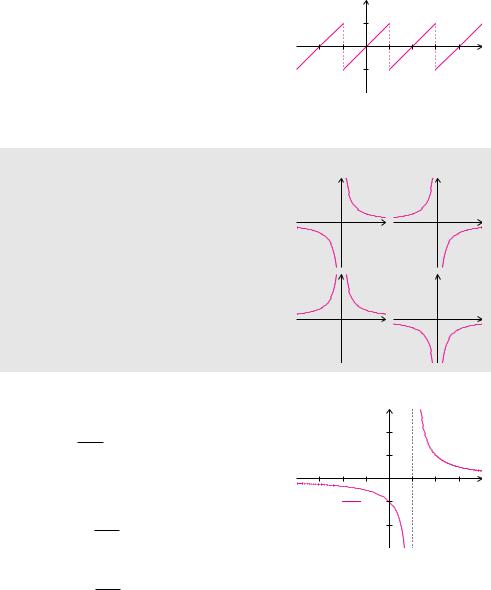
Beispiel 5.57 (Sprungstellen)
Die Funktion
f(x) = x für x [−1, 1], f(x + 2) = f(x)
besteht aus einem Funktionsprototyp über dem Intervall [−1, 1], der mit der Periode 2 auf der Menge der reellen Zahlen fortgesetzt wird. Sie hat unendlich viele Sprungstellen und zwar an den Stellen x = 2 k−1 für k Z.
|
|
y |
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
−2 |
−1 |
1 |
2 |
3 |
4 |
x |
|
||||||
|
|
−1 |
|
|
|
|
Ì
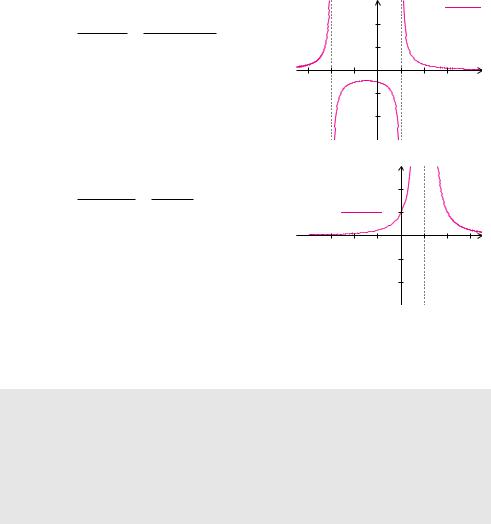
Definition 5.43 (Polstelle, senkrechte Asymptote)
Man nennt die Stelle x0 eine Polstelle oder |
y |
↑ ∞ |
y |
↑ ∞ |
||||||||
kurz Pol einer Funktion f, wenn der linksseiti- |
|
|
||||||||||
ge und der rechtsseitige Grenzwert an der Stelle |
|
|
|
|
||||||||
x0 uneigentliche Grenzwerte |
|
sind. Eine Pol- |
|
x |
|
x |
||||||
stelle ist eine |
Unstetigkeitsstelle 2. Art |
|
|
|
|
|||||||
|
|
±∞ |
|
|
. Das |
−∞ ↓ |
|
−∞ ↓ |
|
|||
Schaubild der Funktion besitzt an einer Polstel- |
|
|
||||||||||
le eine senkrechte Asymptote. Bei Polstellen |
y |
↑ ∞ |
y |
|
||||||||
mit Vorzeichenwechsel findet ein Übergang |
|
|
|
|||||||||
der Funktionswerte von |
|
nach |
|
oder von |
|
|
|
|
||||
|
nach |
|
statt. Bei |
Polstellen ohne Vorzei- |
|
x |
|
x |
||||
∞ |
−∞ |
−∞ |
|
|
∞ |
|
|
|
||||
chenwechsel sind entweder beide uneigentliche |
|
|
−∞ ↓ |
|
||||||||
Grenzwerte ∞ oder beide −∞. |
|
|
|
|
|
|
||||||
Beispiel 5.58 (Polstellen) |
|
|
|
|
|
|
|
|
|
|||
a) |
Die Funktion |
|
|
|
|
|
|
y |
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
2 |
f(x) = x 1 |
|
x 1 eine Definitionslücke. |
|
|
|
|
1 |
||||
hat an |
|
Stelle |
|
|
|
|
|
||||
der − |
|
links an die Definitionslücke |
3 |
2 |
|
1 |
1 2 3 x |
||||
Wenn wir uns von |
= |
|
− |
− |
1 |
− |
|
||||
herantasten, dann erhalten wir |
f (x) = x−1 |
|
1 |
||||||||
|
|
|
|
1 |
= −∞ |
|
|
− |
|||
GL |
|
|
lim |
. |
|
|
|
|
−2 |
||
|
|
1 |
|
|
|
|
|||||
|
= x→1− x |
|
|
|
|
|
|
||||
Auch der |
rechtsseitige Grenzwert |
|
|
|
|
|
|||||
|
− |
|
|
|
|
|
|
|
|||
1
GR = lim = ∞
x→1+ x − 1
ist ein uneigentlicher Grenzwert. An der Stelle x = 1 liegt ein Pol mit Vorzeichenwechsel vor.
210 |
5 Funktionen |
b) |
Die Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
f (x) = |
2 |
1 |
||||
|
|
(x) = x2 |
1 |
|
|
|
= |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x +x−2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
f |
+ |
x |
− |
|
2 |
x |
|
− |
1 x |
+ |
2 |
) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
hat an den |
|
|
|
|
( |
|
|
|
)( |
|
|
|
2 De- |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
beiden Stellen x |
|
|
1 und x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
finitionslücken. Die |
linksseitigen und die rechts- |
3 |
2 |
1 |
|
1 |
2 |
3 |
|
x |
|||||||||||||||||||||||
|
− |
− |
− |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
||||||||||||
|
seitigen Grenzwerte sind an beiden Stellen un- |
|
|
|
−1 |
|
|
|
|
|
||||||||||||||||||||||||
|
eigentliche Grenzwerte und haben unterschiedli- |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
che Vorzeichen. An den Stellen x |
|
1 und x |
= − |
2 |
|
|
|
−2 |
|
|
|
|
|
||||||||||||||||||||
|
liegen Pole mit |
Vorzeichenwechsel vor. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
c) |
Bei der Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|||||
|
f |
x |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
f (x) = x2−2x+1 |
1 |
|
|
|
|
||||||||||
|
|
( ) = x 2 x 1 = |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
ist die |
|
2 |
− |
|
|
+ |
|
( |
|
|
− |
|
|
) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Definitionslücke x 1 eine doppelte Nen- |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
nernullstelle. Der |
linksseitige und der rechtssei- |
|
3 |
2 |
1 |
|
1 |
2 |
|
3 x |
|||||||||||||||||||||||
|
|
− |
− |
− |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
tige Grenzwert ist ein uneigentlicher Grenzwert. |
|
|
|
|
−1 |
|
|
|
|
||||||||||||||||||||||||
|
Sie |
haben |
dasselbe |
Vorzeichen. An |
der |
Stelle |
|
|
|
|
−2 |
|
|
|
|
|||||||||||||||||||
|
x = 1 liegt ein Pol ohne Vorzeichenwechsel vor. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Ì
An der Vielfachheit einer Nennernullstelle einer gebrochenrationalen Funktion, die nicht gleichzeitig eine Zählernullstelle ist, kann man ablesen, ob der zugehörige Pol einen Vorzeichenwechsel hat oder nicht.
Polstellen gebrochenrationaler Funktionen
Ist x0 eine p-fache Nullstelle des Nennerpolynoms einer gebrochenrationalen Funktion und nicht gleichzeitig eine Nullstelle des Zählerpolynoms, so hat die Funktion bei x0 eine Pol. Der Pol hat
Leinen Vorzeichenwechsel, falls p ungerade ist,
Lkeinen Vorzeichenwechsel, falls p gerade ist.
Anschaulich verbirgt sich hinter der Stetigkeit, dass man das komplette Schaubild einer stetigen Funktion ohne Absetzen des Stiftes zeichnen kann. Also können stetige Funktionen keine Werte überspringen. Diese wichtige Eigenschaft stetiger Funktionen ist im Zwischenwertsatz beschrieben. Jeder Wert zwischen zwei Funktionswerten an zwei Stellen wird von einer stetigen Funktion auch angenommen.
