
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

6.4 Geometrische Bedeutung der Ableitungen |
269 |
6.4 Geometrische Bedeutung der Ableitungen
Durch Untersuchung der Ableitungsfunktionen einer Funktion können wir Rückschlüsse auf den Verlauf einer Funktion ziehen. Wir werden sehen, dass die erste Ableitung einer Funktion es ermöglicht, das Steigungsverhalten zu analysieren und Hochund Tiefpunkte zu lokalisieren. Mit der zweiten Ableitung werden wir das Krümmungsverhalten einer Funktion untersuchen.
6.4.1 Neigungswinkel und Schnittwinkel
Die Ableitung beschreibt das Steigungsverhalten einer Funktion. Bei vielen technischen Anwendungen ist es üblich, die Steigung in Form von Winkeln auszudrücken. Der Neigungswinkel einer Funktion wird bezüglich der positiven x-Achse gemessen. Korrekt ausgedrückt handelt es sich nicht um den Neigungswinkel einer Funktion, sondern um den Neigungswinkel des Graphen einer Funktion. Dabei betrachtet man zur Festlegung des Winkels an der Stelle x0 die Tangente an dieser Stelle. Die Gleichung
tan α = f′(x0) = f′(x0).
1
beschreibt die Neigung im rechtwinkligen Steigungsdreieck.
Definition 6.8 (Neigungswinkel)
Der Neigungswinkel des Graphen einer Funktion f im Punkt (x0 S f(x0)) ist der Winkel α, den die Tangente an der Stelle x0 mit der x-Achse bildet. Zwischen dem Winkel α und der Ableitung der Funktion an der Stelle x0 besteht der Zusammenhang
tan α = f′(x0).
y |
|
|
|
f(x0) |
α |
f0 |
(x0) |
|
|
||
1 |
|
|
|
|
|
|
|
x0 |
|
x1 |
x |
Den Neigungswinkel selbst berechnet man mit dem Arkustangens
α = arctan f′(x0).
Der Neigungswinkel α besitzt somit Werte zwischen −π und π . Teilweise wird die Stei-
2 2
gung auch mittels Prozentangaben beschrieben. Prozentangaben entsprechen direkt dem Wert der Ableitung. Beispielsweise entspricht eine Steigung von 10 % dem Ableitungswert 0.1, ebenso entspricht eine Steigung von 100 % dem Ableitungswert 1. Somit sind Steigungen über 100 % gültige Angaben. 200 % Steigung entsprechen einer Steigung von
2, also einem Winkel von arctan 2 ≈ 63○. Für Neigungswinkel, die gegen π streben, geht
2
die Ableitung und somit auch die prozentuale Steigung gegen ∞.
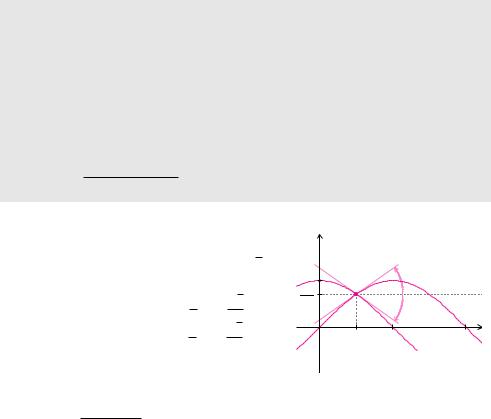
270 |
6 Di erenzialrechnung |
Mithilfe von Tangenten kann man auch einen Winkel zwischen den Schaubildern von zwei Funktionen f und g definieren. Man definiert diesen Winkel als Winkel zwischen den beiden Tangenten. Der Schnittwinkel α ist also die Di erenz der beiden Neigungswinkel αf und αg. Mithilfe der Additionstheoreme für den Tangens, siehe Satz 5.13, erhalten wir
tan α |
tan αf |
αg |
|
tan αf |
− |
tan αg |
|
f |
′ |
( |
x0 |
) − |
g′ |
( |
x0 |
|
. |
||||||||||
= |
( |
− ) = |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
) |
|
||||||||
1 |
+ |
tan |
αf tan αg |
|
+ |
f |
′( |
x0 |
) |
g |
′( |
x0 |
) |
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Definition 6.9 (Schnittwinkel)
Der Schnittwinkel α der Graphen von zwei Funktionen f und g, die sich an der Stelle x0 in einem gemeinsamen Punkt schneiden, ist die Di erenz der beiden Neigungswinkel αf des Schaubildes der Funktion f an der Stelle x0 und αg des Schaubildes der Funktion g an der Stelle x0:
α = αf − αg.
Der Schnittwinkel lässt sich mit den Ableitungen berechnen:
f′(x0) − g′(x0) tan α = 1 + f′(x0) g′(x0).
Beispiel 6.21 (Schnittwinkel) |
|
|
|
|
|
|
|
|
|
|
|||||||||
Die Schaubilder der beiden Funktionen f x |
|
sin x |
y |
|
|
||||||||||||||
und |
g x |
|
|
|
|
cos x |
schneiden sich an der |
Stelle x0 |
π . |
|
|
|
|||||||
( |
) = |
|
( |
) = |
4 |
1 |
|
|
|||||||||||
Die |
|
|
|
|
|
|
|
|
|
|
= |
|
f (x) = sin x |
||||||
|
beiden Ableitungen sind |
|
|
|
|
|
√2 |
|
√2 |
αf |
|
||||||||
|
|
f |
′ |
|
x |
|
cos x |
|
f |
′ |
|
π |
|
|
2 |
αg |
|
||
|
|
|
( ) = |
|
|
Ô |
|
‹ |
4 |
• = |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
′ |
π |
2 |
|
π |
π |
π x |
|||||
|
|
g |
′ |
( ) = − |
sin x |
Ô |
g |
‹ |
4 |
• = − |
2 |
|
4 |
2 |
g(x) = cos x |
||||
|
|
|
|
x |
|
|
|
|
|
|
√ |
|
|
||||||
Somit gilt für den Schnittwinkel |
|
|
|
|
||||||||||
tan α |
|
2 |
√ |
|
1 |
√ |
|
|
2 |
2, |
|
|||
|
|
1 |
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ |
|
2 |
|
|
√ |
|
|
||
|
= |
|
1 |
2 |
|
= |
|
|
|
|||||
|
|
|
|
− |
|
|
|
70 |
○ entspricht. |
Ì |
||||
was einem Winkel von ungefähr |
|
|
||||||||||||
An Stellen, an denen das Produkt der beiden Steigungen den Wert −1 ergibt, können wir mit der Formel aus Definition 6.9 den Schnittwinkel nicht berechnen. Dieser Sonderfall, bei dem der Nenner in der Formel null wird, kennzeichnet zwei senkrecht aufeinander stehende Tangenten.
Ein weiterer Spezialfall liegt vor, falls die Schaubilder zweier Funktionen in einem gemeinsamen Punkt dieselbe Steigung haben. Dann ist der Schnittwinkel null und man spricht von zwei Graphen, die sich berühren.
6.4 Geometrische Bedeutung der Ableitungen |
271 |
Orthogonale und berührende Graphen
Die Graphen der Funktionen f und g, die für x0 denselben Funktionswert haben,
Lstehen genau dann senkrecht zueinander, wenn das Produkt der beiden Ableitungen an der Stelle x0 den Wert −1 ergibt:
f(x0) = g(x0) und f′(x0) g′(x0) = −1.
L berühren sich genau dann, wenn die Ableitungen an der Stelle x0 übereinstimmen: f(x0) = g(x0) und f′(x0) = g′(x0).
6.4.2 Monotonie
Wir haben zwei unterschiedliche Begri e kennengelernt, die das Wachstumsverhalten einer Funktion beschreiben. Zum einen die Monotonie aus Abschnitt 5.3.3 und zum anderen die Ableitung. Wir klären nun den Zusammenhang zwischen diesen beiden Begri en.
Geometrische Bedeutung der ersten Ableitung
Die erste Ableitung an der Stelle x0 beschreibt das Steigungsverhalten einer Funktion f in der unmittelbaren Umgebung der Stelle x0:
f x0 |
¢ |
< |
0 |
Ô |
Funktion fällt |
||
|
|
( |
¨ |
|
|
||
|
′ |
) ¦ |
|
|
|||
|
|
¨ |
|
|
|||
|
|
¨ |
0 |
Funktion wächst. |
|||
|
|
¨ |
|||||
Dabei |
|
|
¤ > |
|
Ô |
|
|
|
betrachtet |
man die Funktion stets in |
|||||
Richtung zunehmender x-Werte.
y
f0 (x0) < 0 f0 (x0) > 0
x
Streng monoton wachsende Funktionen sind somit durch positive Ableitungen und streng monoton fallende Funktionen durch negative Ableitungen charakterisiert.
Erste Ableitung und Monotonie
Falls die erste Ableitung einer Funktion f für alle x-Werte aus einem Intervall I
L positiv ist, dann ist die Funktion auf ganz I streng monoton wachsend:
f′(x) > 0 für alle x I Ô f(x) streng monoton wachsend.
L negativ ist, dann ist die Funktion auf ganz I streng monoton fallend:
f′(x) < 0 für alle x I Ô f(x) streng monoton fallend.

272 |
6 Di erenzialrechnung |
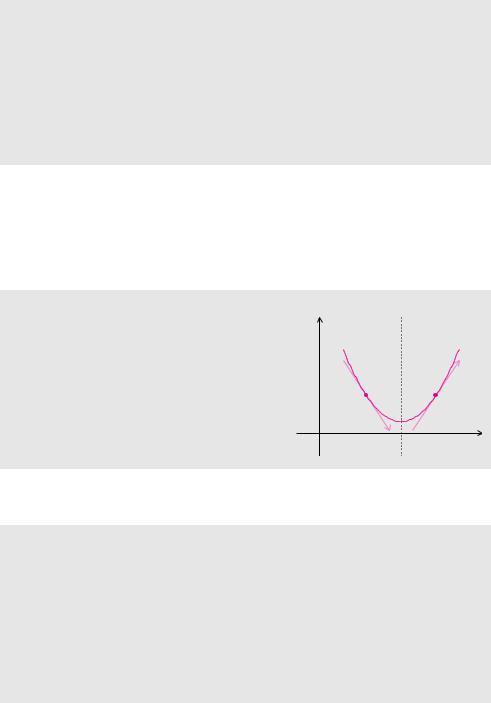
Beispiel 6.22 (Ableitung und Monotonie)
Wir untersuchen das Monotonieverhalten der Funktion
4 x f(x) = 1 + x2 .
Dazu berechnen wir die erste Ableitung mit der Quotientenregel
|
′ |
|
4 |
( |
1 |
+ |
x2 |
) − |
4 x |
|
2 x 4 |
( |
1 |
− |
x2 |
) |
|
|||||||||
f |
|
x |
|
|
|
1 |
|
|
|
|
|
|
|
|
. |
|||||||||||
|
( |
|
|
|
( |
|
+ |
|
2 |
) |
2 |
|
= ( |
|
+ |
|
2 2 |
|||||||||
|
|
) = |
|
|
|
|
x |
|
|
|
1 |
x |
) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y |
|
4 x |
|
|
|
|
f (x) = |
|
||
|
|
|
1+x2 |
|
||
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
−3 |
−2 |
−1 |
1 |
2 |
3 |
x |
|
||||||
|
|
|
−1 |
|
|
|
|
|
|
−2 |
|
|
|
Das Vorzeichen der ersten Ableitung wird von 1 |
|
x2 bestimmt. Für x-Werte zwischen |
1 und |
|
1 |
ist die erste Ableitung positiv und somit ist die |
Funktion f in diesem Bereich streng monoton |
||
|
− |
|
− |
|
wachsend. Außerhalb dieses Bereichs ist die Funktion f streng monoton fallend. |
Ì |
|||
Das Vorzeichen der Ableitung liefert lediglich ein hinreichendes Kriterium für Monotonie. Bei Funktionen, die an gewissen Stellen nicht di erenzierbar sind, muss man deshalb bei der Untersuchung auf Monotonie sorgfältig vorgehen und auf die Definition 5.23 zurückgreifen.
Gilt für die erste Ableitung einer Funktion f die Bedingung f′(x) ≥ 0 auf einem Intervall I, so ist die Funktion zumindest monoton wachsend auf I, allerdings nicht zwingend streng monoton. Gilt entsprechend für die erste Ableitung von f die Bedingung f′(x) ≤ 0, so ist die Funktion monoton fallend auf I, wenn auch nicht zwangsläufig streng monoton.
6.4.3 Krümmung
Auch die zweite Ableitung einer Funktion hat eine anschauliche Bedeutung. Die erste Ableitung beschreibt die Veränderung der Funktion. Auf dieselbe Art beschreibt die zweite Ableitung die Veränderung der Steigung.
Geometrische Bedeutung der zweiten Ableitung |
|
|
|
||||||||
Die zweite Ableitung an der Stelle x0 beschreibt |
y |
f00 (x0) < 0 |
f00 (x0) > 0 |
||||||||
das Krümmungsverhalten einer Funktion f in |
|
|
|
||||||||
der unmittelbaren Umgebung der Stelle x0: |
|
|
|
||||||||
|
|
|
|
¨ |
< |
|
Ô |
Rechtskrümmung, |
|
|
|
f |
|
|
x |
|
|
|
|
|
|||
|
|
|
0 |
¨¨ |
0 |
|
|
|
|
||
|
|
|
|
¨ |
|
|
Steigung nimmt ab |
|
|
|
|
|
′′ |
|
|
¢ |
|
|
|
|
|
||
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
( |
|
¨ |
|
0 |
|
|
|
|
|
|
|
|
) ¦ |
|
|
|
|
|
x |
||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
Linkskrümmung, |
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¨ |
> |
|
Ô |
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
||
|
|
|
|
¨ |
|
|
|
Steigung nimmt zu. |
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
¤ |
|
|
|
|
|
|
|
Auch bei der Beurteilung der Krümmung betrachtet man die Funktion stets in Richtung zunehmender x-Werte. Außerdem ist das Vorzeichen der Steigung zu berücksichtigen. Die
