
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
13.1 Fourier-Analyse |
533 |
Kreisfrequenz ω. Trotzdem ist der Begri Grad gerechtfertigt. Man kann zeigen, dass sich die Funktionen sinn (ω t) und cosn (ω t) als trigonometrische Polynome vom Grad n darstellen lassen.
13.1.3 Fourier-Reihe
In ähnlicher Weise wie beim Übergang von Polynomen zu Potenzreihen bilden wir nun statt einer endlichen eine unendliche Summe. Dadurch entsteht aus einem trigonometrischen Polynom eine sogenannte Fourier-Reihe.
Definition 13.3 (Fourier-Reihe)
Die Darstellung einer Funktion f mit Periode T in Form einer unendlichen Summe von Sinusund Kosinusgliedern
f |
t |
) = |
a0 |
∞ |
ak cos |
( |
k ω t |
bk sin |
( |
k ω t |
)) |
, |
ω |
= |
2 π |
|
2 |
T |
|||||||||||||||
|
( |
+ kQ1 ( |
|
) + |
|
|
|
|
||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
nennt man eine Fourier-Reihe. Die reellen Zahlen ak und bk bezeichnet man als reelle Fourier-Koe zienten.
Trigonometrische Polynome sind Spezialfälle von Fourier-Reihen. Eine Fourier-Reihe, die man nach endlich vielen Gliedern abschneidet, ist ein trigonometrisches Polynom.
Eine Fourier-Reihe ist nur dann sinnvoll definiert, wenn die unendliche Reihe konvergiert. Diese Forderung stellt eine Einschränkung für die Fourier-Koe zienten dar. Von praktischer Bedeutung sind Fourier-Reihen, die man nach endlich vielen Gliedern abschneiden kann, ohne dass die restlichen Glieder einen wesentlichen Einfluss auf die Funktion f haben. Wir fordern deshalb, dass die Koe zienten ak und bk mit wachsendem k schnell genug gegen null gehen.
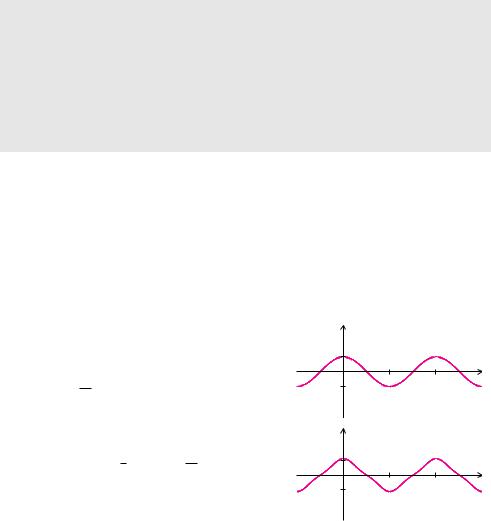
Beispiel 13.5 (Fourier-Reihe)
Wir betrachten eine Fourier-Reihe mit Kreisfrequenz ω = 1, bei der a0 und alle Sinusglieder bk null sind. Die Kosinusglieder ak sind definiert durch:
¢ 1
¨
¨ für k ungerade
¨ k2 ak = ¦¨
¨
¨¤ 0 für k gerade .
Dadurch ergibt sich die Fourier-Reihe
f(t) = cos (t) + 1 cos (3 t) + 1 cos (5 t) + . . .
925
Die Koe zienten der Fourier-Reihe von f gehen sehr schnell gegen null. Die trigonometrischen Polynome vom Grad 3 und 5 stellen eine gute Näherung dar.
cos (t) |
|
|
1 |
|
|
π |
2π |
t |
-1 |
|
|
cos (t) + |
1 cos (3 t) |
|
1 |
9 |
|
|
|
|
π |
2π |
t |
-1 |
|
|

534 |
13 Fourier-Reihen |
Die Fourier-Reihe konvergiert gegen eine Dreieckfunktion mit Periode 2π. Bemerkenswert ist dabei, dass bei der Überlagerung von unendlich vielen di erenzierbaren Sinusund Konsinusfunktionen im Grenzwert eine nicht di erenzierbare Funktion entsteht.
cos (t)+ 1 cos (3t)+ |
1 |
cos (5t) |
|
9 |
25 |
|
|
1 |
|
|
|
π |
2π |
|
t |
-1 |
|
|
|
|
|
|
Ì |
13.1.4 Satz von Fourier
Der französische Mathematiker Jean Baptiste Joseph Fourier hat erkannt, dass man im Prinzip alle periodischen Funktionen mithilfe von den nach ihm benannten Reihen darstellen kann.
Satz 13.1 (Satz von Fourier)
Fast alle Funktionen f mit Periode T lassen sich als Fourier-Reihe
f |
t |
) = |
a0 |
∞ |
ak cos |
( |
k ω t |
bk sin |
( |
k ω t |
)) |
, |
ω |
= |
2 π |
|
2 |
T |
|||||||||||||||
|
( |
+ kQ1 ( |
|
) + |
|
|
|
|
||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
mit den Fourier-Koe zienten ak und bk darstellen.
Die Formulierung „Fast alle Funktionen“ in Satz 13.1 ist für Mathematiker natürlich unbefriedigend. Die Frage, welche periodischen Funktionen sich als Fourier-Reihe darstellen lassen und welche nicht, war in der Mathematik lange Zeit ungeklärt. Letztendlich wurde dieses Problem erst im 20. Jahrhundert endgültig gelöst. Funktionen lassen sich genau dann durch Fourier-Reihen darstellen, wenn sie die sogenannten Dirichlet-Bedingungen erfüllen. Diese Bedingungen gehen auf den Mathematiker Johann Peter Gustav Lejeune Dirichlet zurück. Dazu ist es erforderlich, den hier verwendeten Konvergenzbegri geeignet abzuschwächen. Weitere Einzelheiten dazu findet man beispielsweise bei [Heuser:Analysis].
Wir wollen uns damit begnügen, dass sich jede periodische Funktion von praktischer Bedeutung als Fourier-Reihe darstellen lässt. Bei stetigen Funktionen konvergiert die zugehörige unendliche Reihe an jeder Stelle gegen den entsprechenden Funktionswert. Die Besonderheiten, die bei Fourier-Reihen von periodischen Funktionen mit Unstetigkeitsstellen auftreten, betrachten wir in Abschnitt 13.1.5.
Satz 13.2 (Fourier-Koe zienten)
Die Fourier-Koe zienten ak und bk einer Funktion f mit Periode T und Kreisfrequenz ω = 2Tπ kann man mit den folgenden Formeln berechnen:
L |
|
2 |
|
|
T |
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
ak |
= |
|
|
|
|
− T |
f |
t |
) |
cos k ω t |
dt, |
k |
= |
0, 1, 2, . . . |
|
|
|
|
|
||||||||||||
|
|
|
|
S |
|
( |
( |
) |
|
|
|||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
T |
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
L |
bk = |
|
S− T2 |
f(t) sin(k ω t) dt, |
k = 1, 2, . . . |
||||||||||
T |
|||||||||||||||
13.1 Fourier-Analyse |
535 |
Fourier-Koe zienten lassen sich durch Integralformeln berechnen. Diese Formeln basieren auf der sogenannten Minimaleigenschaft der trigonometrischen Polynome, siehe Abschnitt 13.2.4. Grob formuliert sind Fourier-Koe zienten nichts anderes als Mittelwerte periodischer Funktionen. Der Koe zient a0 ist bis auf den Faktor 2 genau der Mittelwert der periodischen Funktion f. Die übrigen Koe zienten ergeben sich aus den Mittelwerten der Funktion f multipliziert mit den entsprechenden Sinusund Kosinusfunktionen.
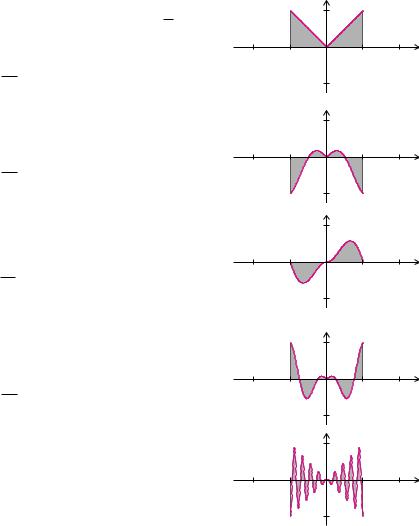
Beispiel 13.6 (Fourier-Reihe einer Dreieckfunktion)
Wir berechnen die Fourier-Reihe der Dreieckfunktion aus Beispiel 13.3. Den Mittelwert m = a20 kann man aus der Fläche unter der Funktion f im Bereich zwischen −π und π berechnen:
a0 = |
2 |
π |
2 π S−π f(t) dt = π. |
||
Den Fourier-Koe zienten a1 berechnet man aus dem Integral über die Funktion f(t) cos(t) für t-Werte zwischen −π und π:
a1 = |
2 |
π |
2 π S−π f(t) cos(t) dt. |
||
Den Fourier-Koe zienten b1 berechnet man aus dem Integral über die Funktion f(t) sin(t) für t-Werte zwischen −π und π:
b1 = |
2 |
π |
2 π S−π f(t) sin(t) dt = 0. |
||
Da f(t) sin(k t) für alle k ungerade Funktionen sind, sind o ensichtlich alle bk null.
Den Fourier-Koe zienten a2 berechnet man aus dem Integral über die Funktion f(t) cos(2 t) für t-Werte zwischen −π und π:
a2 = |
2 |
π |
2 π S−π f(t) cos(2 t) dt. |
||
Für wachsendes k wird die Funktion f durch die hochfrequenten Kosinusfunktionen immer besser abgetastet. Dadurch ergeben sich in etwa gleich viele positive und negative Flächenanteile unter den Funktionen f(t) cos(k t). In Summe kompensieren sich die positiven und negativen Flächenanteile mit wachsendem k immer mehr. Die Fourier-Koe zienten gehen deshalb für wachsendes k gegen null.
π |
|
f (t) |
−2π −π |
π |
2π t |
−π |
|
|
π f (t) cos(t)
−2π −π |
π |
2π t |
−π
π f (t) sin(t)
−2π −π |
π |
2π t |
−π
π f (t) cos(2t)
−2π −π |
π |
2π t |
−π
π f (t) cos(9t)
−2π −π |
π |
2π t |
−π
536 |
13 Fourier-Reihen |
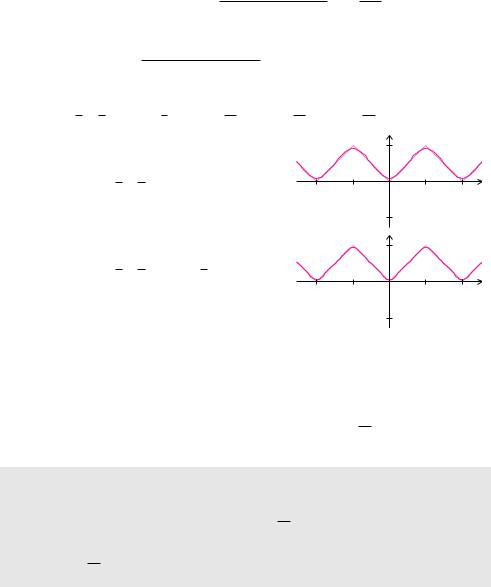
Die Funktionen f(t) und cos(k t) sind beide gerade Funktionen, somit ist das Produkt aus beiden Funktionen wieder eine gerade Funktion. Deshalb kann man die Fourier-Koe zienten einfacher durch die Formel
|
2 |
|
π |
2 |
|
cos |
|
k t |
k t sin |
k t |
|
π |
|
|
|
|
|
|
|
||||||||
ak = |
|
2 S0 |
t cos(k t) dt = |
|
|
‹ |
|
( |
|
) +k2 |
( |
) |
•V0 |
2 π |
π |
|
|
||||||||||
berechnen, siehe Satz 7.9. Dabei haben wir
S x cos (a x) dx = cos (a x) + a x sin (a x) + C a2
= 2 Š(−1)k − 1• k2 π
verwendet und erhalten |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Unter |
f |
t |
) = |
π |
4 |
cos t |
1 cos |
( |
3 t |
) + |
1 cos |
( |
5 t |
) + |
1 |
cos |
( |
7 t |
1 |
cos |
( |
9 t |
) + |
. . . . |
|
|||
|
( |
− |
‹ |
|
( ) + |
|
|
25 |
|
49 |
|
|
) + |
|
|
• |
|
|||||||||||
|
|
|
|
2 |
π |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
81 |
|
|
|
|
|
|
|||
mit |
Berücksichtigung |
der |
Glieder |
bis n |
= |
1, also |
|
|
|
|
|
|
π |
f (t) |
|
|
||||||||||||
f(t) ≈ p1(t) = |
π |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1(t) |
|
||||||||||
|
2 |
− π cos(t), |
|
|
|
|
|
|
|
|
|
|
−2π |
|
−π |
|
|
|
π |
2π |
t |
|||||||
erhalten wir ein gutes Ergebnis. |
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|||||||||
Bei n = 3, also mit |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
π |
4 |
‹cos(t) + |
1 |
|
|
|
|
|
|
|
|
|
|
π |
f (t) |
p3(t) |
|
||||||||||
|
f(t) ≈ p3(t) = |
2 |
− π |
9 cos(3 t)• , |
|
|
|
−2π |
|
−π |
|
|
|
π |
2π |
t |
||||||||||||
ist grafisch kaum ein Unterschied zwischen der Funk- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
tion und der Annäherung durch die Fourier-Reihe zu |
|
|
|
|
|
−π |
|
|
|
|
|
|||||||||||||||||
erkennen. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Die Fourier-Reihe aus Beispiel 13.6 konvergiert sehr schnell gegen die Funktion. Ein paar Reihenglieder genügen, um die Funktion fast fehlerfrei durch die Fourier-Reihe anzunähern. Sichtbar wird die schnelle Konvergenz an der Formel für die Koe zienten. Die Fourier-
1
Koe zienten ak und bk sind in diesem Beispiel proportional zu k2 . Dieses Verhalten ist typisch für stetige Funktionen.
Konvergenz der Fourier-Reihe bei stetigen Funktionen
Bei stetigen periodischen Funktionen konvergiert die Fourier-Reihe schnell. Die Fourier-
1
Koe zienten ak und bk klingen proportional zu k2 ab:
1 ak, bk ≈ k2 .
Die Zerlegung einer periodischen Funktion in Kosinusund Sinusschwingungen bezeichnet man auch als harmonische Analyse. Die harmonische Analyse spielt in der Akustik eine wichtige Rolle. Dabei verwendet man die Begri e Grundschwingung und Oberschwingung.
