
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

392 |
10 Funktionen mit mehreren Variablen |
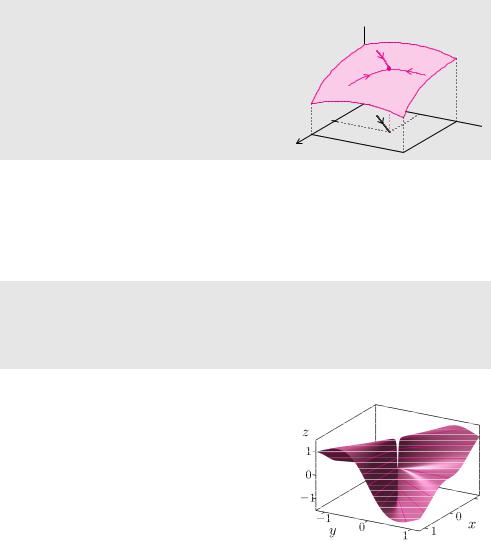
Höhenlinien von Rotationsflächen
Die Höhenlinien von Rotationsflächen sind konzentrische Kreise um den Ursprung.
Beispiel 10.8 (Sombrero)
Die Funktion
sin ‰x2 + y2Ž
f(x, y) =
x2 + y2
besteht aus einem rotationssymmetrischen Sinus, dessen Amplitude mit dem Radius abnimmt. Das
Schaubild hat die Gestalt eines Sombreros. Die Funk- |
|
tion kann mit dem Wert 1 stetig in den Ursprung |
Ì |
fortgesetzt werden. |
10.2 Grenzwert und Stetigkeit
Analog zu Funktionen mit einer Variablen gibt es auch bei Funktionen mit mehreren Variablen den Begri der Stetigkeit. Man muss allerdings gleich erwähnen, dass die Situation hier etwas komplizierter ist. Im Eindimensionalen lautet die anschauliche Definition der Stetigkeit: Eine Funktion ist stetig, wenn man ihr Schaubild ohne abzusetzen zeichnen kann. Diese anschauliche Definition lässt sich nicht ohne Weiteres auf zwei Variablen erweitern.
10.2.1 Grenzwert einer Funktion mit mehreren Variablen
Wir werden im zweidimensionalen Raum keine exakten Definitionen für Folgen und Grenzwerte einführen. Stattdessen beschreiben wir anschaulich, was der Grenzwert
lim |
f |
( |
x, y |
) |
(x,y)→(x0,y0) |
|
|
bedeutet. Der Grenzwert existiert genau dann, wenn bei jeder Annäherung an die Stelle (x0, y0) die Folge der Funktionswerte gegen denselben Grenzwert konvergiert. Dabei müssen wir beachten, dass die Annäherung aus jeder Richtung der x-y-Ebene geschehen kann. Es müssen also viel mehr Möglichkeiten als im Fall einer Variablen geprüft werden.
Bei drei Variablen definiert man den Funktionsgrenzwert durch
lim |
f |
( |
x, y, z |
) |
, |
(x,y,z)→(x0,y0,z0) |
|
|
|
und bei mehr als drei Variablen entsprechend.
10.2 Grenzwert und Stetigkeit |
393 |
Grenzwert einer Funktion
Die Funktion f(x, y) hat an der Stelle (x0, y0) den Grenzwert G, wenn für jede Annäherung von (x, y) an (x0, y0) in einer Umgebung von (x0, y0) die Funktionswerte f(x, y) gegen G konvergieren. Man verwendet die Schreibweise
lim f(x, y) = G.
(x,y)→(x0,y0)
z 
f(x, y)
 y x
y x 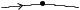


10.2.2 Stetigkeit
Der Begri der Stetigkeit lässt sich formal analog zum eindimensionalen Fall formulieren. Allerdings ist die Interpretation und der Nachweis bei zwei Variablen schwieriger.
Definition 10.3 (Stetigkeit)
Eine Funktion f(x, y) heißt stetig an der Stelle (x0, y0), falls gilt:
lim f(x, y) = f(x0, y0).
(x,y)→(x0,y0)
Beispiel 10.9 (Nicht überall stetige Funktion)
Die Funktion
f x, y |
¢ |
|
3 |
2 für x, y |
0, 0 |
|
|
x24 xy2y |
|
||||||
|
¨ |
− |
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
¨ |
|
|
|
für (x, y) ≠ (0, 0) |
|
|
( |
¨ |
0 |
) |
|
|||
) = ¦ |
( + |
|
|
|
|||
|
¨ |
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
¨ |
x, y |
|
0, 0 stetig,( |
)denn= ( dort) |
ist |
|
ist an allen Stellen¨ |
|
||||||
|
¤ |
|
|
|
|
|
|
( ) ≠ ( )
sie eine Verkettung von elementaren, stetigen Funktionen. An der Stelle 0, 0 können wir die Annähe-
rung aus den beiden Achsenrichtungen untersuchen: |
||||||
|
0 |
( |
) |
0 |
|
|
lim |
= 0 |
lim |
. |
|||
|
|
|||||
x=0,y→0 y4 |
= y=0,x→0 x4 |
|||||
Man könnte nun vermuten, f wäre stetig im Ursprung. Dazu müssen aber auch alle anderen Annäherungen an den Ursprung denselben Grenzwert haben. Wir betrachen die Annäherungen entlang der Winkelhalbierenden y = ±x:
lim |
4 x4 |
1 |
≠ |
1 |
lim |
4 x4 |
. |
|
|
|
|
|
|
|
|
||||||
y=x→0 −4 x4 = − |
|
|
= y=−x→0 4 x4 |
|
− |
|
||||
Es ergeben sich also mindestens die drei verschiedenen Grenzwerte 0, |
1 und 1. Der Grenzwert |
|||||||||
ist nicht eindeutig, also ist f im Ursprung nicht stetig. |
Ì |
|||||||||

394 |
|
|
|
|
|
|
|
|
|
|
|
10 Funktionen mit mehreren Variablen |
Bei drei Variablen definiert man die Stetigkeit durch |
||||||||||||
lim |
f |
( |
x, y, z |
) = |
f |
( |
x |
0 |
, y |
0 |
, z |
0) |
(x,y,z)→(x0,y0,z0) |
|
|
|
|
|
|
||||||
und bei mehr als drei Variablen entsprechend.
Üblicherweise sind Funktionen, die bei praktischen Problemstellungen auftauchen, stetig. Alle elementaren Funktionen sind auch in mehreren Veränderlichen stetig. Der Nachweis der Stetigkeit einer Funktion geschieht in der Regel durch die Argumentation, dass die Funktion aus einfachen, elementaren Funktionstermen, die ihrerseits stetig sind, zusammengesetzt ist.
Unstetigkeitsstellen entstehen typischerweise bei zusammengesetzen Funktionen. Zum Nachweis der Unstetigkeit einer Funktion gibt man eine Stelle an, an der es zwei Richtungen gibt, aus denen die Annäherungen an diese Stelle zu verschiedenen Grenzwerten führen, siehe Beispiel 10.9.
10.3 Di erenziation
Wie im Fall von Funktionen einer Variablen behandeln wir nach der Stetigkeit nun die Di erenzierbarkeit. Was ist, anschaulich gesprochen, die Ableitung einer Funktion mit zwei Variablen an einer Stelle (x0, y0)?
10.3.1 Partielle Ableitungen und partielle Di erenzierbarkeit
Um die Ableitung einer Funktion mit mehreren Variablen mathematisch zu definieren, müssen wir zunächst die partielle Ableitung einführen. Wir haben in Abschnitt 10.1 gesehen, dass es für das Verständnis einer Funktion mit mehreren Variablen günstig ist, zunächst eine Variable festzuhalten. Auf diese Weise sind wir zu Schnittkurven gekommen. Auch hier machen wir uns die Situation zunächst etwas einfacher und halten eine Variable fest.
Definition 10.4 (Partielle Ableitung)
Die partielle Ableitung der Funktion f(x, y) nach x bzw. nach y an der Stelle (x0, y0) ist folgendermaßen definiert:
L |
fx |
( |
x0, y0 |
) = |
lim |
f |
( |
x0 |
+ |
x, y0 |
) − |
f |
( |
x0 |
, y0 |
) |
||||
|
|
|
→ |
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
L |
fy |
( |
x0, y0 |
) = |
lim |
|
f |
( |
x0, y0 |
+ |
y |
) − |
f |
( |
x0 |
, y0 |
) |
|||
|
|
|
→ |
0 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
y |
|
|
|
|
|
|||
Dazu müssen die entsprechenden Grenzwerte existieren.
10.3 Di erenziation |
395 |
Beispiel 10.10 (Partielle Ableitung)
Die Funktion
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x, y) = x1,+2y |
|
|
partiellen Ableitungen |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
hat an der Stelle ( |
) die |
‰( |
1 |
+ |
|
x |
2 |
|
4 |
Ž − ( |
1 |
+ |
4 |
) |
|
|
|
|
|
|
|
|
|||||
|
( |
|
) = |
|
x 0 |
|
|
) +x |
|
|
= |
x 0 |
|
|
|
) = |
|
||||||||||
fx |
1, 2 |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
2 |
|
x |
2 |
||||||
|
|
|
|
→ |
1 |
|
2 |
+ |
y |
) |
2 |
Ž − ( |
1 |
+ |
4 |
) |
→ |
( + |
|
|
|||||||
|
( |
|
) = |
|
|
→ |
‰ |
+ ( |
|
|
|
|
|
= |
→ |
( |
|
+ |
|
) = |
|
||||||
fy |
|
1, 2 |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
4 |
|
y |
|
4 |
||
|
|
|
|
|
y 0 |
|
|
|
|
|
|
y |
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
||
Partielle Ableitungen
Die partielle Ableitung
Lfx(x0, y0) entspricht gerade der Steigung der Schnittkurve parallel zur x-z-Ebene an der Stelle (x0, y0),
Lfy(x0, y0) entspricht gerade der Steigung der Schnittkurve parallel zur y-z-Ebene an der Stelle (x0, y0).
z 
f(x, y)
fy
fx 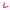
x
Ì
y
Für die partiellen Ableitungen gibt es verschiedene Notationen. Je nach Kontext ist eher die Indexschreibweise oder eher die Di erenzialschreibweise günstig. Um deutlich zu machen, dass es sich um partielle Ableitungen handelt, verwendet man in der Di erenzialschreibweise die Notation ∂ anstelle von d. Wie im Eindimensionalen ist der Grenzwert des Di erenzenquotienten also ein Di erenzialquotient.
Definition 10.5 (Di erenzialquotient)
Für die partiellen Ableitungen sind verschiedene Schreibweisen gebräuchlich:
L |
|
∂f |
|
||
fx(x0, y0) = |
|
|
V(x0,y0) |
= Dx fS(x0,y0) |
|
∂x |
|||||
L |
|
∂f |
|
||
fy(x0, y0) = |
|
V(x0,y0) |
= Dy fS(x0,y0) |
||
∂y |
|||||
Die jeweils zweite Form heißt Di erenzialquotient.
Hieraus können wir unmittelbar den Begri der partiellen Di erenzierbarkeit gewinnen. Ist der Grenzwert der partiellen Ableitungen an einer Stelle (x0, y0) vorhanden, so ist die Funktion an dieser Stelle partiell di erenzierbar.

396 |
10 Funktionen mit mehreren Variablen |
Definition 10.6 (Partielle Di erenzierbarkeit)
Die Funktion f heißt partiell di erenzierbar nach x bzw. y
Lan der Stelle (x0, y0), falls die partielle Ableitung fx bzw. fy an der Stelle (x0, y0) existiert.
Lauf der Menge M R2, falls die partielle Ableitung fx bzw. fy auf der Menge M R2 existiert.
Ist eine Funktion auf einer Menge partiell di erenzierbar, so entsteht durch die partielle Ableitung an allen Punkten dieser Menge eine neue Funktion.
Definition 10.7 (Partielle Ableitungsfunktion)
Bei einer partiell di erenzierbaren Funktion f(x, y) kann man neue Funktionen fx(x, y) bzw. fy(x, y) dadurch definieren, dass man jeder Stelle (x, y) die Steigung der Tangente in x-Richtung bzw. y-Richtung zuordnet:
(x, y) ( fx(x, y), (x, y) ( fy(x, y).
Diese Funktionen bezeichnet man als partielle Ableitungsfunktion in x bzw. in y.
Durch die partiellen Ableitungen entstehen also zwei neue Funktionen fx, fy R2 → R. Schauen wir uns die Definition der partiellen Ableitung an, so wird deutlich, dass wir für die praktische Berechnung der partiellen Ableitung keine neuen Rechenregeln benötigen. Es ist lediglich etwas Konzentration nötig, um nach der gewünschten Variablen abzuleiten und die andere dabei festzuhalten.
Berechnung der partiellen Ableitungen
Bei der Berechnung der partiellen Ableitungen geht man folgendermaßen vor:
L |
Zur Bestimmung von fx x, y |
|
stellt man sich y als Konstante vor und berechnet |
|||||||||||||||||||||||
die Ableitung der |
Funktion mit der Variablen x. |
|||||||||||||||||||||||||
|
|
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|||||||||
L |
Zur Bestimmung von fy |
|
|
x, y |
|
stellt man sich x als Konstante vor und berechnet |
||||||||||||||||||||
die Ableitung der |
Funktion mit der Variablen y. |
|||||||||||||||||||||||||
|
|
|
|
( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
||||||||
Beispiel 10.11 (Berechnung der partiellen Ableitungen) |
||||||||||||||||||||||||||
a) |
Die Funktion f |
( |
x, y |
) = |
e−x |
|
cos y hat die partiellen Ableitungen |
|||||||||||||||||||
|
( |
|
) = − |
− |
|
|
|
|
|
|
|
(y |
|
) = − |
e |
− |
x sin y. |
|||||||||
|
fx |
x, y |
|
|
e |
x cos y, |
|
fy |
x, y |
|
|
|
|
|
||||||||||||
b) |
Die Funktion |
f |
( |
x, y |
) = |
arctan |
|
|
|
hat |
die partiellen Ableitungen |
|||||||||||||||
|
y |
|
|
|
|
|
|
x |
|
x |
y2 . |
|||||||||||||||
|
fx |
x, y |
|
x2− y2 , fy |
|
|
x, y |
|
|
|
|
x2 |
|
|
||||||||||||
|
( |
|
) = |
|
|
+ |
|
|
|
( |
|
|
|
|
) = |
|
|
+ |
|
|
|
|||||

10.3 Di erenziation |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
397 |
|||||||
c) |
Die Funktion f |
|
x, y |
|
» |
|
|
|
|
|
|
|
hat die partiellen Ableitungen |
|
||||||||||||||||||
( |
|
1 |
− |
x2 |
− |
y2 |
|
|||||||||||||||||||||||||
|
fx x, y |
|
|
|
|
|
)x= |
y2 |
|
x, y |
|
|
|
1 |
|
y |
|
y2 . |
Ì |
|||||||||||||
|
|
|
1 |
−x2 |
|
, fy |
|
|
|
|
−x2 |
|
||||||||||||||||||||
|
( |
|
) = |
» |
|
|
− |
|
− |
|
|
|
|
|
|
( |
|
) = |
» |
|
|
− |
|
− |
|
|
|
|||||
Ableitung der Schnittkurven |
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Die Schnittkurven einer Funktion z |
|
|
f |
x, y |
|
haben folgende Ableitungen: |
|
|||||||||||||||||||||||||
L |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
=1 |
|
|
|
) y |
|
0 |
|
|
|
|||||
x x |
|
g y |
|
f x , y , g |
′ |
y |
|
|
f x , y |
|
||||||||||||||||||||||
y = y0 |
g2(x) = f(x, y0), g2(x) = fx(x, y0) |
|
||||||||||||||||||||||||||||||
L |
= |
|
|
|
|
|
( ) = ( |
|
|
) |
|
|
|
|
′ ( ) = ( |
|
) |
|
||||||||||||||
10.3.2 Di erenzierbarkeit und Tangentialebene
Nachdem wir die partielle Di erenzierbarkeit, also die Di erenzierbarkeit in Richtung der Achsen, untersucht haben, betrachten wir nun die sogenannte totale Di erenzierbarkeit. Dazu wählen wir eine anschauliche Definition.
Definition 10.8 (Di erenzierbarkeit)
Eine Funktion f(x, y) heißt di erenzierbar an einer Stelle (x0, y0), wenn sie dort eine eindeutige Tangentialebene besitzt.
Für den Test, ob eine Funktion di erenzierbar ist oder nicht, gibt es ein gut nachprüfbares Kriterium. Dieses ist sogar notwendig und hinreichend, enthält also eine genau-dann-wenn- Bedingung.
Satz 10.1 (Di erenzierbarkeit)
Eine Funktion f(x, y) ist genau dann di erenzierbar auf einer Menge M R2, wenn beide partiellen Ableitungen auf M existieren und stetig sind.
Beispiel 10.12 (Rotationsparaboloid)
Wir betrachten das Rotationsparaboloid
f(x, y) = x2 + y2.
Die Funktion ist auf ganz R2 di erenzierbar und damit insbesondere stetig. Die partiellen Ableitungen
fx |
x, y |
2 x, fy x, y |
|
2y |
|||
existieren |
(überall) =und sind stetig.( ) =Die Funktion f be- |
||||||
sitzt an jeder Stelle |
( |
x0, y0 |
) |
R |
2 eine Tangential- |
||
ebene. |
|
|
|
Ì |
|||
398 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 Funktionen mit mehreren Variablen |
|
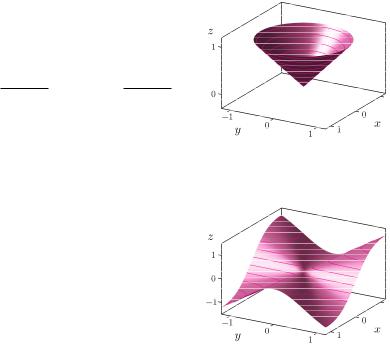
Beispiel 10.13 (Kegel) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Wir betrachten die auf ganz R2 definierte Funktion |
|||||||||||||||||||
|
|
» |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
f x, y |
x2 |
|
|
y2 |
|
|
|
|
|
|
|
|
||||||
Die partiellen( |
)Ableitungen= + |
|
|
|
|
|
|
|
|
||||||||||
|
fx(x, y) = |
» |
|
x |
|
|
|
, fy(x, y) = |
» |
y |
|
||||||||
|
|
|
|
||||||||||||||||
|
x2 y2 |
x2 y2 |
|||||||||||||||||
existieren an der Stelle |
|
|
0, 0 |
|
nicht, denn die |
einseiti- |
|||||||||||||
|
+ |
|
|
|
+ |
|
|||||||||||||
gen Grenzwerte der |
Steigungen sind |
|
1. Die Funktion |
||||||||||||||||
|
|
( ) |
|
|
, 0 |
|
|
|
|
||||||||||
f |
ist di erenzierbar für |
|
|
x, y |
|
0 |
|
|
|
Ì |
|||||||||
|
|
( |
|
|
|
) ≠ ( |
|
± . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
||
Beispiel 10.14 (Funktion mit unstetigen partiellen Ableitungen)
Wir betrachten die Funktion
f |
x, y |
|
¢ |
|
|
2 x y2 |
|
für |
|
x, y |
|
|
0, 0 |
|
|
|
|
|||||||
|
x2 |
|
|
y2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
¨ |
|
− |
|
0 |
|
|
|
für |
|
x, y |
|
|
0, 0 . |
|
|
|||||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
( |
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
( |
|
|
) ≠ ( |
|
) |
|
|
|
|
|
) = ¦ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
( |
|
|
) = ( |
|
) |
|
|
|
|
Sie ist für |
x, y |
¨ |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
¤ |
0 0 |
|
di erenzierbar und damit |
|||||||||||||||||||
insbesondere stetig. Die partiellen Ableitungen |
|
|
|
|
||||||||||||||||||||
|
|
( |
|
) ≠ ( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
fx |
|
x, y |
|
¢ |
|
|
|
2 |
|
|
2 |
|
2 |
für |
|
x, y |
|
0, 0 |
|
|||||
|
|
|
2yx2x |
|
y2y2 |
|
|
|
||||||||||||||||
|
|
|
|
¨ |
|
|
|
|
( |
0 |
− |
) |
für |
|
x, y |
|
0, 0 |
|
||||||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
( |
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
( ) ≠ ( |
|
|
) |
||||
|
|
) = ¦ |
|
|
( |
|
|
+3 |
y |
) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
¨ |
|
|
|
4 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
(x, y) = ( |
|
|
) |
||||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||
|
|
|
|
¤ |
|
|
|
|
|
|
|
|
|
|
für |
|
|
|
|
|
0 |
0 |
|
|
fy |
|
x, y |
|
|
|
x2 |
|
|
y2 |
2 |
|
|
|
|
|
|
|
|||||||
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
¨ |
|
|
− |
|
0 |
|
|
|
|
für |
|
|
x, y |
|
|
0, 0 |
|
|||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
( |
) ≠ ( |
) |
||||||||
|
( |
|
|
¨ |
( + |
|
) |
|
|
|
|
|
|
|
||||||||||
|
|
) = ¦ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) = ( |
|
|
) |
||
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
¤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
existieren an der |
kritischen Stelle |
|
0, 0 . In Beispiel 10.9 haben wir gesehen, dass zumindest fy an |
||||||||||||
¨ |
Also ist die Funktion f |
x, y |
|
an der Stelle |
0, 0 stetig, aber nicht |
||||||||||
der Stelle |
0, 0 |
|
nicht stetig ist. |
|
|||||||||||
( |
) |
|
( |
) |
|
( |
|
) |
( |
) |
|
||||
di |
|
|
|
|
|
|
|
|
|
||||||
|
erenzierbar. Sie besitzt an der Stelle |
0, 0 keine Tangentialebene. Dies wird auch anschaulich |
|||||||||||||
deutlich, wenn man das Schaubild der |
Funktion betrachtet. |
|
|
Ì |
|||||||||||
( ) |
|
|
|
|
|
||||||||||
Wir diskutieren die Frage, wie man eine Ebene an einen Punkt (x0, y0) einer Fläche z = f(x, y) so anlegt, dass die Steigungen von Funktion und Ebene zumindest in den Achsenrichtungen gleich sind.
Existieren die partiellen Ableitungen fx(x0, y0) und fy(x0, y0), so bezeichnen sie die Steigungen von f in x-Richtung und in y-Richtung an der Stelle (x0, y0). Steigungsvektoren in x-Richtung und in y-Richtung an der Stelle (x0, y0) sind
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
fx |
x0 |
, y0 |
|
|
||
vx |
’ |
|
|
|
0 |
|
|
|
“ |
, vy |
’ |
|
|
|
1 |
|
|
|
“ |
n vx vy |
’ |
−fy |
(x0 |
, y0) |
“ |
. |
||
|
f |
x |
|
x |
0 |
, y |
0 |
|
|
f |
y |
|
x |
0 |
, y |
0 |
|
|
|
|
|
|
||||||
|
=– |
|
( |
|
|
) |
— |
|
=– |
|
( |
|
|
) |
— Ô = × =– − ( 1 |
) — |
|
|||||||||||
|
” |
|
|
|
|
|
|
• |
|
” |
|
|
|
|
|
|
• |
|
” |
|
|
|
• |
|
||||
Der Normalenvektor n steht senkrecht auf beiden Steigungsvektoren und ergibt sich deshalb aus dem Vektorprodukt, siehe Definition 3.9.
