
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
12.4 Schwingungsdi erenzialgleichungen |
491 |
Beispiel 12.35 (Allgemeine Lösung bei Resonanz)
Die Di erenzialgleichung
y′′ + 9 y = 6 sin 3 x
besitzt die Eigenwerte λ1,2 = ±3 i und somit die allgemeine Lösung der homogenen Gleichung
yh(x) = C1 cos 3 x + C2 sin 3 x.
Der Störfunktion r(x) = 6 sin 3 x sind ebenfalls die Eigenwerte λ = ±3 i zugeordnet. Es liegt also Resonanz vor. Der Ansatz für eine partikuläre Lösung laut Störansatztabelle wird mit dem Faktor x multipliziert:
yp(x) = A1 x cos 3 x + A2 x sin 3 x.
Zum Einsetzen in die Di erenzialgleichung verwenden wir das Tableau
|
|
|
yp |
x |
= |
A1 cos 3 x |
A1 x cos 3 x |
|
A2 sin 3 x |
+ |
A2 x sin 3 x |
9 |
|
|||
|
|
|
yp |
(x) |
3 A2 x cos 3 x |
|
3 A1 x sin 3 x |
S (0) |
||||||||
|
|
|
′ |
(x) |
= |
6 A2 cos 3 x |
+ 9 A1 x cos 3 x |
+ |
6 A1 sin 3 x |
− |
9 A2 x sin 3 x |
S (1) |
||||
|
|
|
yp |
|||||||||||||
|
|
|
′′( ) = |
|
− |
− |
|
|
|
− |
|
S ( ) |
||||
|
|
|
6 sin 3 x |
|
|
6 A2 cos 3 x |
|
|
6 A1 sin 3 x |
|
|
|
|
|||
|
|
|
|
|
für A1 und A2 |
kommen keine Terme mit x sin 3 x und x cos 3 x vor. Es folgt |
||||||||||
In der Gleichung = |
|
|
− |
|
|
|
|
|
|
|
||||||
A1 |
|
1 und A2 |
= |
0. Eine partikuläre Lösung lautet also yp |
( |
x |
x cos 3 x. Setzt man homogene |
|||||||||
und= − |
|
|
|
|
|
|
|
|
) = − |
|
|
|
|
|||
|
partikuläre Lösung zusammen |
|
|
|
|
|
|
|
|
|||||||
|
|
|
y(x) = C1 cos 3 x + C2 sin 3 x − x cos 3 x, |
|
|
|
|
|
|
|
|
|||||
so erhält man die allgemeine Lösung der Ausgangsdi erenzialgleichung. |
Ì |
|||||||||||||||
12.4 Schwingungsdi erenzialgleichungen
Schwingungsdi erenzialgleichungen sind lineare Di erenzialgleichungen zweiter Ordnung mit konstanten Koe zienten. Ihr Verhalten ist trotz ihrer Einfachheit vielfältig, sodass man verschiedene Phänomene, die bei Di erenzialgleichungen auftreten können, studieren kann. In Anwendungen treten Schwingungsdi erenzialgleichungen an vielen Stellen auf. So kann ein mechanischer Schwinger ebenso wie ein elektrischer Schaltkreis als Schwingungsdi erenzialgleichung modelliert werden, siehe Abschnitt 12.7.
12.4.1 Allgemeine Form
Die allgemeine Form einer Schwingungsdi erenzialgleichung enthält zwei verschiedene Parameter. Der sogenannte Dämpfungsfaktor berücksichtigt Phänomene, die Einfluss auf die Dämpfung des Schwingungsverhaltens haben. Beispiele dafür sind die Reibung bei mechanischen Schwingungen oder der Widerstände bei elektrischen Schaltkreisen. Größen,

492 |
12 Gewöhnliche Di erenzialgleichungen |
die Auswirkungen auf die Schwingungsdauer bei periodischen Vorgängen haben, werden durch die sogenannte Kreisfrequenz berücksichtigt. Beispiele dafür sind Federkonstanten oder Massen bei mechanischen Schwingungen und Induktivitäten oder Kapazitäten in elektrischen Schaltkreisen.
Definition 12.19 (Schwingungsdi erenzialgleichung)
Eine Di erenzialgleichung, die man in der Form
x¨ + 2 δ x˙ + ω02 x = r(t)
schreiben kann, nennt man eine Schwingungsdi erenzialgleichung mit der Dämpfung δ ≥ 0 und der Kreisfrequenz ω0 > 0.
Der Faktor 2 vor dem δ und das Quadrat bei ω0 sind so gewählt, dass die Formeln für die Lösungsfunktionen möglichst einfach werden. Für δ wird auch die Bezeichnung Abklingkonstante verwendet. Bei ω0 handelt es sich genau genommen um die Kreisfrequenz der ungedämpften Schwingung. Bei gedämpften Schwingungen hängt die Schwingungsdauer sowohl von der Kreisfrequenz ω0 als auch von der Dämpfung δ ab.
In den Beispielen in Abschnitt 12.7.4 und Abschnitt 12.7.6 entstehen die Störfunktion durch Einwirkung von außen. Ein Feder-Masse-Schwinger ohne Erregerkraft und ein elektrischer Schwingkreis ohne eine angelegte Spannungsquelle werden durch eine homogene Di erenzialgleichung beschrieben. Auch ohne Anregung von außen sind die Systeme schwingungsfähig. Beispielsweise kann man beim Feder-Masse-Schwinger die Masse aus der Ruhelage heraus auslenken. Die so erzeugte Spannungsenergie bringt das System zum Schwingen. Einen ähnlichen E ekt hat ein geladener Kondensator im elektrischen Schwingkreis.
Im homogenen Fall überlässt man das System sich selbst. Man spricht dabei auch von einer freien Schwingung. Im inhomogenen Fall erfolgt eine äußere Anregung. Diese Anregung hat maßgeblichen Einfluss auf das Verhalten des Systems. Deshalb bezeichnet man diesen Fall auch als erzwungene Schwingung.
Definition 12.20 (Freie und erzwungene Schwingung)
Eine homogene Schwingungsdi erenzialgleichung bezeichnet man als freie Schwingung, eine inhomogene als angeregte oder erzwungene Schwingung.
12.4.2 Freie Schwingung
Die Schwingungsdi erenzialgleichung aus Definition 12.19 ist eine lineare Di erenzialgleichung mit konstanten Koe zienten. Aus der charakteristischen Gleichung
λ2 + 2 δλ + ω02 = 0

12.4 Schwingungsdi erenzialgleichungen |
493 |
können wir die allgemeine Lösung der homogenen Gleichung berechnen. In Abhängigkeit von der Dämpfung δ und der Kreisfrequenz ω0 betrachten wir vier verschiedene Fälle.
Eigenwerte der Schwingungsdi erenzialgleichung
Die Schwingungsdi erenzialgleichung hat die beiden Eigenwerte
|
|
|
|
¼ |
|
|
|
|
|
|
|
|
|
|||||
|
|
λ1,2 |
δ |
δ2 |
ω02 |
. |
|
|
|
|
|
|
|
|||||
Deshalb unterscheidet= − ± |
−man vier Fälle: |
|
|
|
|
|
|
|
||||||||||
(A) |
Keine Dämpfung: δ |
= |
0 |
(B) |
Schwache Dämpfung: 0 |
δ ω0 |
||||||||||||
(C) |
Grenzfall: δ |
|
ω0 |
|
|
(D) |
|
|
|
δ |
|
ω |
||||||
= |
|
|
Sehr starke Dämpfung: < |
> |
<0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(A) Keine Dämpfung: δ |
|
0 |
|
|
|
|
i ω rein imaginär und die |
|||||||||||
Für |
δ |
|
0 |
, also ohne |
|
Dämpfung, sind beide Eigenwerte λ |
1,2 |
|
||||||||||
|
= |
|
|
|
|
= |
|
|
|
= ± |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
allgemeine Lösung der homogenen Di erenzialgleichung
x(t) = C1 cos ω0 t + C2 sin ω0 t
besteht aus harmonischen Schwingungen mit der Kreisfrequenz ω0.
(B) Schwache Dämpfung: 0 |
δ |
|
ω0 |
|
||||||||
|
|
|
|
|
|
|
|
für 0 |
δ ω , bilden die Eigenwerte |
|||
Bei schwacher Dämpfung, also < |
|
< |
< < |
0 |
||||||||
λ1,2 |
|
δ |
|
i ¼ |
|
|
|
|
|
|
|
|
= − |
± |
ω02 |
− |
δ2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
ein konjugiert komplexes Paar. Die allgemeine Lösung
x(t) = e−δ t (C1 cos ωδ t + C2 sin ωδ t)
besteht nun aus gedämpften harmonischen Schwingungen mit der Kreisfrequenz
¼
ωδ = ω02 − δ2.
Die Kreisfrequenz ωδ der gedämpften harmonischen Schwingung hängt also sowohl von der Dämpfung δ als auch von der Kreisfrequenz ω0 ab. In der Literatur werden leider unterschiedliche Bezeichnungen verwendet. Manchmal spricht man nur dann von schwacher Dämpfung, wenn δ deutlich kleiner als ω0 ist. Ist δ nur unwesentlich kleiner als ω0 wählt man die Bezeichnung starke Dämpfung.
(C) Grenzfall: δ = ω0
Für δ = ω0 hat die Di erenzialgleichung einen doppelten reellen Eigenwert λ1,2 = −δ und die allgemeine Lösung lautet
x(t) = e−δ t (C1 + C2 t) .
Das System ist nicht mehr in der Lage zu schwingen.
494 |
12 Gewöhnliche Di erenzialgleichungen |
(D) Sehr starke Dämpfung: δ > ω0
Im Fall von δ > ω0¼hat die Di erenzialgleichung zwei verschiedene negative reelle Eigenwerte λ1,2 = −δ ± δ2 − ω02 und die Lösungen
x(t) = C1 eλ1 t + C2 eλ2 t
bestehen aus der Überlagerung von zwei abklingenden Exponentialfunktionen. Aus
¼
λ1 = −δ + δ2 − ω02 < −δ + δ = 0
erkennt man, dass tatsächlich beide Eigenwerte negativ sind. Dieser Fall wird in der Literatur manchmal auch als starke Dämpfung bezeichnet.
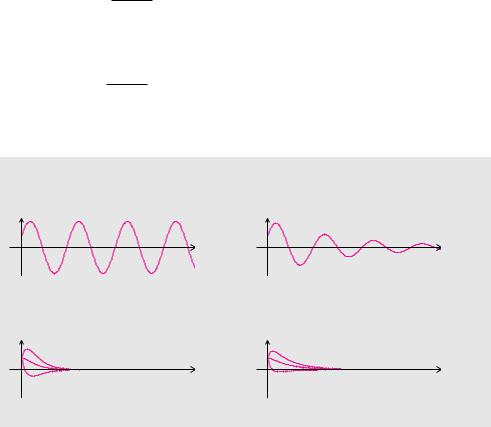
Freie Schwingungen
(A) Keine Dämpfung: δ |
= |
0 |
|||
x |
|
|
|
|
|
|
|
|
|
|
t |
x(t) = C1 cos ω0 t + C2 sin ω0 t |
|||||
(C) Grenzfall: δ |
= |
ω |
0 |
|
|
x |
|
|
|
||
x(t) = e−δ t (C1 + C2 t) |
|
t |
|||
|
|
||||
(B) Schwache Dämpfung: 0 |
< |
δ |
< |
ω |
0 |
|
x |
|
|
||||
|
|
|
t |
|
|
|
x(t) = e−δ t (C1 cos ωδ t + C2 sin ωδ t) |
||||||
(D) Sehr starke Dämpfung: δ |
> |
ω |
0 |
|
||
x |
|
|
|
|||
x(t) = C1 eλ1 t + C2 eλ2 t |
|
|
t |
|
|
|
|
|
|
|
|
|
|
Der qualitative Verlauf der Lösungsfunktionen ist im Grenzfall und im Fall sehr starker Dämpfung ähnlich. Abhängig von den Konstanten C1 und C2 haben die Funktionen höchstens eine Nullstelle und höchstens eine Extremstelle.
12.4.3 Harmonisch angeregte Schwingung
Bei praktischen Problemstellungen treten Schwingungen typischerweise dann auf, wenn ein schwingungsfähiges System eine Anregung von außen erfährt. Bewegungen am Aufhängepunkt der Feder beim Feder-Masse-Schwinger aus Abschnitt 12.7.4 stellen eine äußere Anregung dar. Bei einer Maschine erzeugt beispielsweise ein Elektroantrieb eine Anregung von außen. Beim elektrischen Schwingkreis aus Beispiel 12.7.6 ist die Spannungsquelle Ursache für eine äußere Anregung. Im mathematischen Modell erzeugen diese äußeren Anregungen eine inhomogene Di erenzialgleichung mit einer Störfunktion r. Bei Schwingungsproblemen in der Praxis treten ganz unterschiedliche Störfunktionen r auf. Oft findet die Anregung in Form einer harmonischen Schwingung statt. Deshalb untersuchen wir

12.4 Schwingungsdi erenzialgleichungen |
495 |
Schwingungsdi erenzialgleichungen mit Störfunktionen in Form harmonischer Schwingungen ausführlich. Auch wenn die Anregung in Wirklichkeit nicht in Form einer harmonischen Schwingung stattfindet, lässt sich durch Fourier-Reihen, siehe Kapitel 13, eine Annäherung durch harmonische Schwingungen realisieren. Das Problem kann dann nach dem Superpositionsprinzip gelöst werden.
Definition 12.21 (Harmonisch angeregte Schwingung)
Eine Di erenzialgleichung der Form
x¨ + 2 δ x˙ + ω02 x = ω02 xE cos (ωE t)
bezeichnet man als harmonisch angeregte Schwingung. Dabei bezeichnet xE > 0 die Erregeramplitude und ωE > 0 die Erregerkreisfrequenz.
Der Faktor ω02 wird in die Störfunktion aufgenommen, um einfachere Lösungsformeln für die partikuläre Lösung xp zu erzeugen. Laut Störansatztabelle ist
xp(t) = A1 cos (ωE t) + A2 sin (ωE t)
ein geeigneter Ansatz für eine partikuläre Lösung. In der Schwingungslehre verwendet man jedoch typischerweise den Ansatz
xp(t) = A cos (ωE t − ϕ), ϕ ≥ 0.
Beide Ansätze sind aus mathematischer Sicht gleichwertig. Der Ansatz aus der Schwingungslehre berücksichtigt, dass die partikuläre Lösung der Erregerfunktion mit derselben Frequenz, aber mit einer Phasenverschiebung, nachläuft. Dieses Nachlaufen ist auch der Grund für den Ansatz (ωE t − ϕ) im Gegensatz zu unserer bisherigen Schreibweise (ωE t + ϕ), siehe Definition 5.28 und Satz 11.17. Unser Ziel ist es, Formeln herzuleiten, die die Amplitude A und den Phasenwinkel ϕ in Abhängigkeit von δ, ω0, ωE und xE darstellen.
Der Fall δ = 0, also der ungedämpfte Fall, hat für praktische Problemstellungen wenig Bedeutung. In der Mechanik wird immer Reibung auftreten und in elektrischen Schwingkreisen sind die Widerstände nicht zu vernachlässigen. Trotzdem hilft diese idealisierte Annahme, um Rückschlüsse über ein schwingungsfähiges System zu erhalten.
Satz 12.11 (Harmonisch angeregte, ungedämpfte Schwingung)
Eine harmonisch angeregte Schwingung mit δ |
= |
0 besitzt die partikuläre Lösung |
|||||||||||||||
|
|
¨ |
|
ω02 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω02 |
ωE2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
¢ |
xE cos ωE t |
) |
|
für |
ωE |
< |
ω0 |
||||||||
xp |
t |
¨ |
|
1 |
ω t |
|
x |
|
( |
π |
|
|
ω |
ω |
|||
¨ |
|
|
|
|
ω t |
|
|
|
|
|
|||||||
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) = ¦ |
|
|
|
|
E cos |
|
|
|
für |
|
|
|
||||
|
|
¨ |
|
2 |
−0 |
2 |
|
E |
− |
2 |
E |
= |
0 |
||||
|
|
¨ |
|
2 |
|
|
xE cos(ωE t |
π ) |
für |
ωE |
ω0 . |
||||||
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
E |
|
ω |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
( |
− |
) |
|
|
|
> |
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

496 |
12 Gewöhnliche Di erenzialgleichungen |
Diese Formel lässt sich herleiten, indem man den Schwingungslehreansatz zusammen mit
x˙p(t) = −ωE A sin (ωE t − ϕ), x¨p(t) = −ωE2 A cos (ωE t − ϕ)
in die Di erenzialgleichung der harmonisch angeregten Schwingung einsetzt:
−ωE2 A cos (ωE t − ϕ) + ω02 A cos (ωE t − ϕ) = ω02 xE cos (ωE t).
Für ωE < ω0 löst ϕ = 0 diese Gleichung, indem man durch cos (ωE t) teilt:
( |
ω2 |
− |
ω2 |
) |
A |
= |
ω2 xE |
Ô |
A |
= |
ω02 |
xE. |
ω02 − ωE2 |
||||||||||||
|
0 |
|
E |
|
|
|
0 |
|
|
|
|
|
Im Fall von ωE > ω0 liefert ϕ = π mit cos (ωE t − π) = − cos (ωE t) die Lösung:
( |
ω2 |
− |
ω2 |
) |
A |
= |
ω2 xE |
Ô |
A |
= |
ω02 |
xE. |
|
ωE2 − ω02 |
|||||||||||||
E |
o |
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Für ωE = ω0 liegt Resonanz vor. In diesem Fall führt unser Ansatz nicht zum Ziel. Die Lösung ergibt sich durch einen Resonanzansatz, bei dem der bisherige Ansatz mit t multiplizert wird. Dadurch ergibt sich eine partikuläre Lösung xp mit Phasenwinkel ϕ = π2 , bei der die Amplitude mit wachsender Zeit über alle Grenzen anwächst. Die Details führen wir hier jedoch nicht durch.
Satz 12.12 (Harmonisch angeregte, gedämpfte Schwingung )
Eine harmonisch angeregte Schwingung mit δ > 0 besitzt die partikuläre Lösung
|
|
ω2 xE |
|
|
2 δ ωE |
||
0 |
|
|
|
|
|||
xp(t) = |
» |
|
cos(ωE t − ϕ), |
tan ϕ = |
|
. |
|
ω02 − ωE2 |
|||||||
(ω02 − ωE2 )2 + 4 δ2 ωE2 |
|||||||
Ein Weg zur Bestimmung einer partikulären Lösung führt über die sogenannte Komplexifizierung der Di erenzialgleichung. Dabei fassen wir die ursprüngliche Di erenzialgleichung als Realteil einer komplexen Di erenzialgleichung auf. Wir ergänzen die Störfunktion durch einen entsprechenden Imaginärteil und bezeichnen die komplexe Lösung mit z:
z¨ + 2 δ z˙ + ω02 z = ω02 xE ‰ cos (ωE t) + i sin (ωE t)Ž = ω02 xE ei ωE t.
In dieser komplexen Form kann man
zp(t) = A ei (ωE t−ϕ), z˙p(t) = i A ωE ei (ωE t−ϕ), z¨p(t) = −A ωE2 ei (ωE t−ϕ)
als partikuläre Lösung ansetzen. Nach dem Einsetzen dieses Ansatzes in die Schwingungsdi erenzialgleichung kann man den Term ei ωE t kürzen und erhält
−A ωE2 e−i ϕ + 2 δ i A ωE e−i ϕ + ω02 A e−i ϕ = ω02 xE.
Diese Gleichung kann man so umstellen, dass auf der linken Seite eine komplexer Ausdruck in kartesischer Form und auf der rechten Seite in Exponentialform steht:
2 |
2 |
|
ω2 xE |
|
i ϕ |
|
|
0 |
|
|
|||
(ω0 |
− ωE) + i (2 |
δ ωE) = |
|
e |
|
. |
A |
|
12.4 Schwingungsdi erenzialgleichungen |
|
|
|
|
|
|
|
|
497 |
|||||||||||
Aus einem Vergleich von linker mit rechter Seite folgt ϕ |
0, π . Außerdem ergibt sich |
|||||||||||||||||||
für die Amplitude A und den Winkel ϕ |
|
|
|
|
2 δ ωE [ |
] |
|
|||||||||||||
¼ |
|
|
|
|
|
|
|
|
|
ω02 xE |
|
|
|
|
|
|||||
|
ω02 |
− |
ωE2 |
) |
2 |
+ |
4 δ2 ωE2 |
= |
|
tan ϕ |
= |
|
||||||||
|
|
, |
|
|
|
|
. |
|
|
|||||||||||
|
A |
ω02 |
− |
ωE2 |
|
|
||||||||||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Im Spezialfall ωE = ω0 ist ϕ = π2 und es liegt Resonanzfähigkeit vor. Die Stärke der Resonanz hängt von der Dämpfung ab. Deshalb spricht man hier auch im Unterschied zum ungedämpften Fall nicht von Resonanz, sondern lediglich von Resonanzfähigkeit.
Definition 12.22 (Unterkritische und überkritische Anregung)
Eine harmonisch angeregte, gedämpfte Schwingung bezeichnet man als
Lunterkritisch, falls die Erregerfrequenz ωE kleiner als die Kreisfrequenz ω0 ist. In diesem Fall liegt die Phasenverschiebung ϕ zwischen 0 und π2 .
Lüberkritisch, falls die Erregerfrequenz ωE größer als die Kreisfrequenz ω0 ist. In diesem Fall liegt die Phasenverschiebung ϕ zwischen π2 und π.
Phasenverschiebungen lassen sich durch Experimente sehr gut beobachten. So kann man die Resonanzfähigkeit eines Systems experimentell bestimmen.
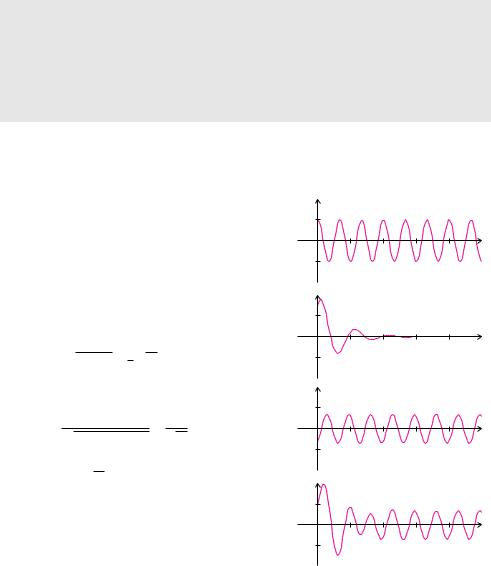
Beispiel 12.36 (Harmonisch angeregte, gedämpfte Schwingung)
Bei der Schwingungsdi erenzialgleichung |
|
|
|
|
|
x |
|
xE cos (ωE t) |
|
|
||||||||||||||||||||||||
|
|
x¨ |
|
|
x˙ |
|
4 x |
|
8 cos 3 t |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
handelt |
es sich um ein schwach gedämpftes Problem |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
+ |
|
|
+ |
|
|
|
|
=1 |
|
und Kreisfrequenz ω0 |
|
|
2. Die |
|
π |
2π |
3π |
4π |
t |
||||||||||||||
mit Dämpfung δ |
|
|
|
2 |
|
|
|
−2 |
|
|
|
|
|
|||||||||||||||||||||
Erregerkreisfrequenz ist ωE |
|
|
3 und die Erregeram- |
|
|
|
|
|
|
|||||||||||||||||||||||||
plitude xE |
|
|
2. |
|
|
= |
|
|
|
|
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||
Die |
homogene Lösung lautet |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
= |
|
|
e− |
1 |
|
|
C1 cos ωδ t |
+ |
C1 cos ωδ t |
) |
|
|
xh(t) |
|
|
|||||||||||||||
|
|
xh |
|
t |
|
|
|
2 t |
|
2 |
|
|
|
|
|
|||||||||||||||||||
mit der |
Kreisfrequenz |
|
|
|
|
|
|
|
|
|
|
|
|
π |
2π |
3π |
4π |
t |
||||||||||||||||
|
|
( ) = |
|
|
|
|
|
( |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
»ω02 |
|
|
δ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
||||||
|
|
ωδ |
= |
− |
= |
2 √15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
) = |
A cos |
3 t |
− |
ϕ |
) hat |
x |
|
|
|
|
|
||||||||||
Die partikuläre Lösung xp |
|
|
|
|
|
|
||||||||||||||||||||||||||||
die Amplitude |
|
|
|
|
|
8 |
|
|
( |
8 |
( |
|
|
|
2 |
|
xp(t) |
|
|
|||||||||||||||
|
|
A = » 22 32 2 32 = √34 . |
|
|
|
|
|
|
|
−2 |
π |
2π |
3π |
4π |
t |
|||||||||||||||||||
Bei |
überkritischer Anregung liegt die Phasenverschie- |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
( |
|
|
|
−3 |
|
) |
+ |
|
|
|
|
π |
und π. |
|
|
|
|
|
|
|
|
|||||||
bung ϕ |
|
|
arctan |
|
|
|
5 |
|
|
π zwischen 2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
allgemeinen Lösung, die durch Überlagerung |
x |
x(t) = xh(t) + xp(t) |
|
|||||||||||||||||||||||||||||
Bei der = |
|
|
|
|
|
|
|
‰ |
− |
|
Ž |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
der homogenen und der partikulären Lösung entsteht, |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||
tritt nach einer gewissen Zeit ein sogenannter einge- |
|
|
|
|
|
|
||||||||||||||||||||||||||||
schwungener oder stationärer Zustand ein. Die ex- |
−2 |
π |
2π |
3π |
4π |
t |
||||||||||||||||||||||||||||
ponentiell gedämpfte homogene Lösung spielt nur zu |
|
|
|
|
|
|||||||||||||||||||||||||||||
Beginn der Schwingung eine Rolle. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Ì
