
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
222 |
5 Funktionen |
5.7 Umkehrfunktionen
Eine Umkehrfunktion hebt die Wirkung einer Funktion wieder auf. Dieses Prinzip kennen wir bereits vom Begri der Wurzel. Das Wurzelziehen hebt die Wirkung des Quadrierens auf und umgekehrt. Wenn wir die Wurzel aus einer Zahl quadrieren, dann erhalten wir wieder die ursprüngliche Zahl. In diesem Abschnitt nehmen wir zunächst das Prinzip der Umkehrfunktion genauer unter die Lupe und wenden es dann auf eine Reihe elementarer Funktionen an.
5.7.1 Das Prinzip der Umkehrfunktion
Eine Funktion muss gewisse Voraussetzungen erfüllen, damit man ihr eine Umkehrfunktion zuordnen kann. Wenn unterschiedliche x-Werte denselben Funktionswert haben, dann kann man das Prinzip der Umkehrfunktion nicht anwenden.
Definition 5.53 (Umkehrbare Funktion)
Eine Funktion f nennt man umkehrbar auf dem Definitionsbereich D, wenn es zu jedem Funktionswert y aus dem Wertebereich W genau ein Argument x aus dem Definitionsbereich D gibt mit y = f(x).
In Definition 5.2 ist die Eigenschaft der Bijektivität einer Funktion eingeführt worden. Nach Definition 5.53 ist eine Funktion genau dann umkehrbar, wenn sie bijektiv ist.
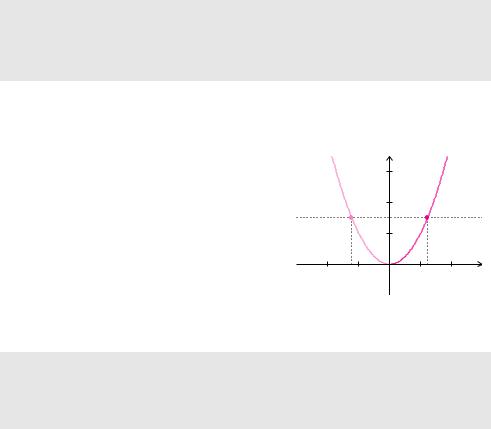
Beispiel 5.65 (Umkehrbare Funktion) |
|
|
|
|
|
|
|||||||||
Die Funktion f x |
|
x2 ist für alle reellen Zahlen de- |
y |
|
|
||||||||||
diesem Definitionsbereich nicht um- |
3 |
|
|
||||||||||||
finiert, aber auf( ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kehrbar. Denn zu jedem positiven y-Wert gibt es zwei |
|
|
|
||||||||||||
verschiedene x-Werte mit f x |
|
y. Wenn wir jedoch |
2 |
f(x) =x2 |
|||||||||||
|
|
|
|
|
|
|
das Intervall D |
|
0; |
|
|
|
|
||
den Definitionsbereich auf ( |
) = |
|
|
besei- |
1 |
|
|
||||||||
|
|
|
|
|
diese |
Mehrdeutigkeit |
|
|
|
||||||
einschränken, dann |
|
ist |
|
x |
2 |
|
|
= [ ∞) |
|
|
|
||||
tigt. Die Funktion f |
( |
x |
) = |
|
ist auf diesem Intervall |
|
|
|
|||||||
umkehrbar. |
|
|
|
|
|
|
|
−2 −1 |
1 |
2 |
x |
||||
Ì
Funktionen mit geeigneten Monotonieeigenschaften sind umkehrbar. So ist die strenge Monotonie hinreichend für die Umkehrbarkeit einer Funktion.
Satz 5.23 (Umkehrbarkeit einer Funktion)
Eine Funktion, die auf dem gesamten Definitionsbereich D entweder streng monoton wachsend oder auf dem gesamten Definitionsbereich D streng monoton fallend ist, ist auf dem Definitionsbereich D umkehrbar.

5.7 Umkehrfunktionen |
223 |
Zu jeder umkehrbaren Funktion können wir eine Umkehrfunktion definieren. Dabei fordern wir, dass die Anwendung der Umkehrfunktion auf die Funktion die Wirkung der Funktion gerade aufhebt und umgekehrt.
Definition 5.54 (Umkehrfunktion, inverse Funktion)
Die Umkehrfunktion oder inverse Funktion f−1 einer umkehrbaren Funktion f ist definiert durch
f−1 (f(x)) = x und f ‰f−1(x)Ž = x.
Die Komposition von Funktion und Umkehrfunktion erzeugt gerade wieder das Ausgangselement. Bildet man also zunächst x auf f(x) ab und wendet auf das Ergebnis anschließend f−1 an, so erhält man wieder x zurück. Die Umkehrfunktion darf nicht mit dem Kehrwert einer Funktion verwechselt werden!
Beispiel 5.66 (Umkehrfunktionen) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a) |
Die Funktion f x |
|
|
|
x2 |
ist auf dem Definitionsbereich D |
|
|
|
0; |
|
umkehrbar, siehe Bei- |
|||||||||||||||||||
|
2 |
|
|
( ) = |
|
|
2 |
|
= |
− |
( ) = |
√ |
|
= [ |
|
∞) |
|
|
|
|
|||||||||||
|
spiel 5.65. Die |
|
|
|
|
|
|
1 x |
|
x, denn |
|
|
|
|
|
|
|||||||||||||||
|
√ |
|
|
|
|
|
Umkehrfunktion ist f |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
= x und ‰√ |
|
|
Ž |
|
|
= x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
b) |
x |
|
|
x |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R streng monoton |
|||||||||
Die Funktion f x |
|
|
|
x |
|
ist auf dem gesamten Definitionsbereich D |
|
|
|||||||||||||||||||||||
|
3 |
|
|
3 |
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
= |
f |
− |
1 |
( ) = |
√ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
wachsend und |
somit umkehrbar. Die Umkehrfunktion ist |
|
x |
3 |
x, denn |
|||||||||||||||||||||||||
|
( |
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||||||||
|
√ |
|
|
|
= x und ‰√ |
|
Ž = x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Nachdem festgestellt ist, dass eine Funktion umkehrbar ist, stellt sich die Frage, wie die Umkehrfunktion dann auch bestimmt werden kann. Die Umkehrfunktion kann grafisch oder auch rechnerisch bestimmt werden.
Bestimmung der Umkehrfunktion
Man bestimmt die Umkehrfunktion einer umkehrbaren Funktion f in zwei Schritten:
(1)Durch Auflösen der Funktionsgleichung y = f(x) nach x erhält man x = f−1(y).
(2)Vertauschen von x und y ergibt eine neue Funktion y = f−1(x).
Durch das Vertauschen von x und y werden Definitionsbereich und Wertebereich vertauscht. Das Schaubild der Umkehrfunktion erhält man durch Spiegeln des Schaubildes der Funktion an der ersten Winkelhalbierenden.

224 |
5 Funktionen |
Beispiel 5.67 (Bestimmung der Umkehrfunktionen)
Die Funktion f x |
|
x |
nimmt jeden Wert y ihres |
|
x |
|
|||
|
|
1 |
||
genau einmal an. Damit ist sie auf ih- |
||||
Wertebereichs ( ) = |
umkehrbar. Zur Bestimmung |
|||
rem Definitionsbereich + |
|
|
||
der Umkehrfunktion lösen wir die Funktionsgleichung nach x auf und erhalten
|
|
y = |
x |
|
Ô x = |
y |
. |
||||
|
|
x 1 |
|
1 y |
|||||||
Durch |
Vertauschen von x und y entsteht die Um- |
||||||||||
|
|
+ |
|
|
|
|
− |
||||
kehrfunktion f−1 x |
|
x |
. Geometrisch entsteht |
||||||||
|
1 x |
||||||||||
f 1 |
aus |
f |
durch |
Spiegelung an der ersten Winkelhal- |
|||||||
|
|
( |
) = |
− |
|||||||
bierenden.− |
|
|
|
|
|||||||
|
|
y |
f −1 (x) |
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
f (x) |
|
|
|
|
|
|
|
|
−3 |
−2 |
−1 |
1 |
2 |
3 |
x |
|
||||||
|
|
−1 |
|
|
|
|
|
|
−2 |
|
|
|
|
Ì
5.7.2 Wurzelfunktionen
Die Überlegungen aus Beispiel 5.66 lassen sich auf alle Potenzfunktionen mit natürlichen Hochzahlen übertragen. Potenzfunktionen mit geraden Hochzahlen sind auf dem Intervall [0, ∞) streng monoton wachsend und damit umkehrbar. Potenzfunktionen mit ungeraden Hochzahlen sind auf der Menge der reellen Zahlen streng monoton wachsend und damit umkehrbar.
Definition 5.55 (Wurzelfunktionen)
Die Wurzelfunktionen sind die Umkehrfunktionen der Potenzfunktionen:
f(x) = xn f−1(x) = |
√x = xn . |
||
|
n |
|
1 |
|
|
|
|
Dabei ist n eine natürliche Zahl.
Auch für die Wurzelfunktionen können wir einige grundlegende Eigenschaften zusammenfassen. Eine Besonderheit ist hier der Definitionsbereich, der vom Exponenten abhängt.
Eigenschaften der Wurzelfunktionen
LDefinitionsbereich:
D = [0, ∞) falls n gerade, D = R falls n ungerade
LWertebereich: W = [0, ∞)
LMonotonie: streng monoton wachsend
y |
x2 |
|
|
|
3 |
|
|
√x |
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
1 |
2 |
3 |
4 |
x |

5.7 Umkehrfunktionen |
225 |
5.7.3 Arkusfunktionen
Die Umkehrfunktionen der trigonometrischen Funktionen bezeichnet man als Arkusfunktionen. Aufgrund der Periodizität sind die trigonometrischen Funktionen auf der Menge der reellen Zahlen sicherlich nicht umkehrbar. Für die Umkehrfunktion muss man jede trigonometrische Funktion auf ein Teilintervall einschränken, in dem sie streng monoton ist.
Der Sinus ist zwischen −π2 und π2 streng monoton wachsend und somit auf diesem Intervall umkehrbar. Der Kosinus ist zwischen 0 und π streng monoton fallend und somit auf diesem Intervall umkehrbar.
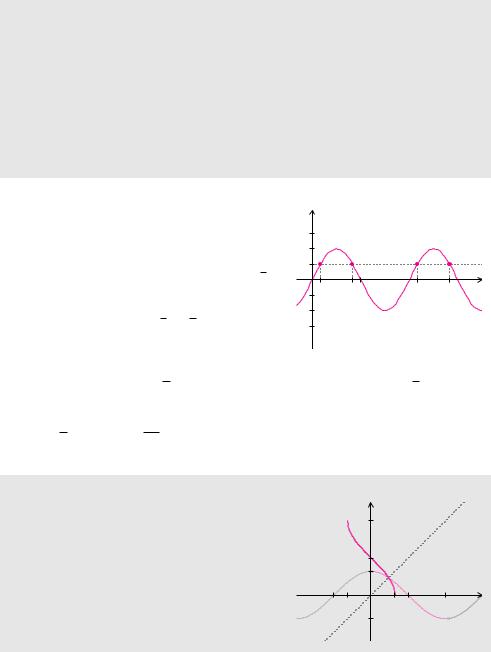
Definition 5.56 (Arkussinus und Arkuskosinus)
Die Umkehrfunktion des Sinus auf dem Intervall [−π2 , π2 ] nennt man Arkussinus:
f(x) = sin x f−1(x) = arcsin x.
Die Umkehrfunktion des Kosinus auf dem Intervall [0, π] nennt man Arkuskosinus:
f(x) = cos x f−1(x) = arccos x.
Grafisch erhält man den Arkussinus durch Spiegelung des Sinus an der ersten Winkelhalbierenden. Dementsprechend kann man auch die Eigenschaften des Sinus in die Eigenschaften des Arkussinus transformieren.
Eigenschaften des Arkussinus
LDefinitionsbereich: D = [−1, 1]
LWertebereich: W = [−π2 , π2 ]
LSymmetrie: zum Ursprung
LMonotonie: streng monoton wachsend
LNullstelle: x = 0
|
y |
|
|
|
||
|
|
arcsin x |
|
|
||
|
π |
|
|
|
||
|
2 |
|
|
|
||
|
|
1 |
|
|
|
|
|
|
sin x |
|
|
||
π |
−1 |
1 |
π |
π |
x |
|
− 2 |
2 |
|||||
|
|
|||||
|
|
1 |
|
|
|
|
|
−π |
|
|
|
||
|
− |
2 |
|
|
|
|
Beispiel 5.68 (Werte des Arkussinus)
a) |
Es ist arcsin |
1 |
|
π |
, denn sin |
|
π |
1 . |
||||||||
|
|
‹ |
|
• = |
|
|
π |
‹ |
|
• = |
|
|
|
|||
|
|
|
|
|
2 |
|
||||||||||
|
|
2 |
6 |
|
|
|
6 |
|
|
|
|
|||||
b) |
Es ist arcsin (−1) = − |
|
, denn sin ‹− |
π |
• = −1. |
|||||||||||
|
|
|
||||||||||||||
|
|
|||||||||||||||
22
c)Der Ausdruck arcsin (π) ist nicht definiert. Die Zahl π liegt nicht im Definitionsbereich des
Arkussinus. |
Ì |
226 |
5 Funktionen |
Mithilfe des Arkussinus lassen sich Gleichungen auflösen, die den Sinus enthalten. Er wird meistens dann verwendet, wenn aus einem bekannten Sinuswert zugehörige Winkel bestimmt werden sollen.
Gleichungen lösen mit Arkussinus
Der Sinus ist nur auf der halben Periode umkehrbar. Um alle Lösungen der Gleichung
sin x = y
zu |
bestimmen, berechnet man die erste Lösung |
direkt mit dem Arkussinus, also |
|||||
x0 |
= |
arcsin y. Die zweite Lösung ergibt sich durch x1 |
= |
π |
− |
arcsin y. Alle Lösungen |
|
ergeben sich wegen der Periode 2π zu |
k Z. |
|
|
||||
|
|
x = arcsin y + 2 k π, x = π − arcsin y + 2 k π, |
|
|
|||
Beispiel 5.69 (Arkussinus)
Wir suchen alle x-Werte, für die die Funktion |
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||||
f x |
|
2 sin x |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
f (x) = 2 sin x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
( |
) = |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
1 |
|
|
|
|
|
|
|
|||
den Funktionswert 1 hat. Auf die Gleichung sin x |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
wenden wir den Arkussinus an |
|
|
|
|
|
1 |
x0 |
x1 π |
|
|
x2 |
x3 |
x |
|||||||||
|
|
|
|
|
|
|
|
1 |
π . |
|
|
|
|
|
− |
|
|
|
|
|
|
|
arcsin |
sin x |
|
arcsin |
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
2 |
6 |
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
) = |
|
|
‹ |
• = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Die erste Lösung ist somit x0 |
|
|
π . Wegen sin |
|
π |
|
x0 |
|
sin x0 ist auch x1 |
|
π |
π ein gesuchter |
||||||||||
x |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
ergeben sich wegen der Periode 2 π zu |
|
= |
|
− |
|
|
||||||||||||
-Wert. Alle Lösungen |
|
|
= |
|
|
( |
|
− |
|
) = |
|
|
|
|
|
|
||||||
x = |
π |
|
|
5 π |
+ 2 π k, k Z. |
|
|
|
|
|
|
|
|
|
|
Ì |
||||||
6 + 2 π k, x = |
6 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Eigenschaften des Arkuskosinus
LDefinitionsbereich: D = [−1, 1]
LWertebereich: W = [0, π]
LSymmetrie: zum Punkt ‰0, π2 Ž
LMonotonie: streng monoton fallend
LNullstelle: x = 1
|
|
y |
|
|
|
|
|
|
π |
|
|
|
|
arccos x |
|
|
|
|
||
|
|
π |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
− |
π |
−1 |
1 |
π |
π |
x |
2 |
2 |
|
||||
|
|
−1 |
|
|
cos x |
|

5.7 Umkehrfunktionen |
|
|
|
|
|
|
|
|
|
|
227 |
|||||||||
Beispiel 5.70 (Werte des Arkuskosinus) |
|
|
|
|
||||||||||||||||
a) |
Es ist arccos |
|
1 |
|
|
|
|
2 π |
, denn cos |
|
|
2 π |
• = − |
1 |
. |
|||||
2 |
|
|
|
|
3 |
|
3 |
2 |
||||||||||||
b) |
Es ist arccos |
|
|
|
|
|
|
|
|
|
||||||||||
‹− • =, denn |
cos |
0 |
‹ . |
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
||||
|
|
arccos |
|
|
π |
|
|
|
definiert, da π |
nicht im Definitionsbereich des Arkuskosinus |
||||||||||
c) |
Der Wert |
|
( ) = |
|
|
• |
ist nicht ( |
) = |
|
|
|
|
Ì |
|||||||
|
|
|
|
|
|
|
||||||||||||||
|
liegt. |
|
|
|
‹ |
2 |
|
|
|
|
|
|
|
|
2 |
|||||
Beispiel 5.69 zeigt, dass man beim Lösen einer trigonometrischen Gleichung mit dem Arkussinus sehr sorgfältig vorgehen muss, damit man nicht einen Teil der Lösungen verliert. Das Lösen trigonometrischer Gleichungen mit dem Arkuskosinus verläuft analog zum Vorgehen beim Arkussinus. Wichtig hierbei ist wiederum die Mehrdeutigkeit des gesuchten Winkels.
Gleichungen lösen mit Arkuskosinus
Der Kosinus ist nur auf der halben Periode umkehrbar. Um alle Lösungen der Gleichung
cos x = y
zu bestimmen, berechnet man die erste Lösung direkt mit dem Arkuskosinus, also x0 = arccos y. Die zweite Lösung ergibt sich durch x1 = −arccos y. Alle Lösungen ergeben sich wegen der Periode 2π zu
x = arccos y + 2 k π, x = −arccos y + 2 k π, k Z.
Beispiel 5.71 (Arkuskosinus) |
|
|
|
|
|
|
|
|
|
|||||||||
Wir suchen alle Nullstellen der Funktion |
|
|
|
y |
|
|
|
|||||||||||
f |
( |
x |
2 |
− |
4 cos |
2 |
x. |
|
|
|
|
|
|
2 |
f (x) =2−4 cos2x |
|||
|
) = |
|
|
|
|
|
|
|
|
1 |
. |
|
1 |
|
|
|
||
Diese x-Werte erfüllen die Gleichung cos x |
= ± √2 |
|
|
|
|
|
||||||||||||
Mit dem Arkuskosinus erhalten wir |
|
x3 |
x2 |
1 |
x0 |
π |
x1 x |
|||||||||||
|
|
= |
|
|
|
Π|
1 |
‘ |
= |
|
|
|
− |
|
|
|
||
x0 |
|
arccos |
π , |
|
|
−2 |
|
|
|
|||||||||
|
|
|
|
|
√ |
4 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
1 |
‘ |
= |
5 π |
|
|
|
|
|
|
|
x1 |
|
arccos Œ−√2 |
4 . |
|
|
|
|
|
|
|
||||||||
Die entsprechenden negativen Werte x2 |
|
|
π |
und x3 |
|
5 π |
sind auch Nullstellen der Funktion |
||||||||||
|
4 |
4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Alle Lösungen ergeben sich wegen der |
Periode 2 π zu |
= − |
|
|
|
||||||||||||
|
= − |
|
|
|
|
|
|
|
|
||||||||
|
π |
5 π |
|
|
|
|
|
π |
|
|
|
5 π |
|
|
|||
x = |
|
+ 2 π k, x = |
|
+ 2 π k, x |
= − |
|
+ 2 π k, x = − |
|
+ 2 π k, k Z. |
Ì |
|||||||
4 |
4 |
4 |
4 |
||||||||||||||
Im Gegensatz zum Sinus und zum Kosinus ist der Tangens auf der vollen Periode streng monoton wachsend und somit umkehrbar. Dies gilt auch für den Kotangens.
228 |
5 Funktionen |
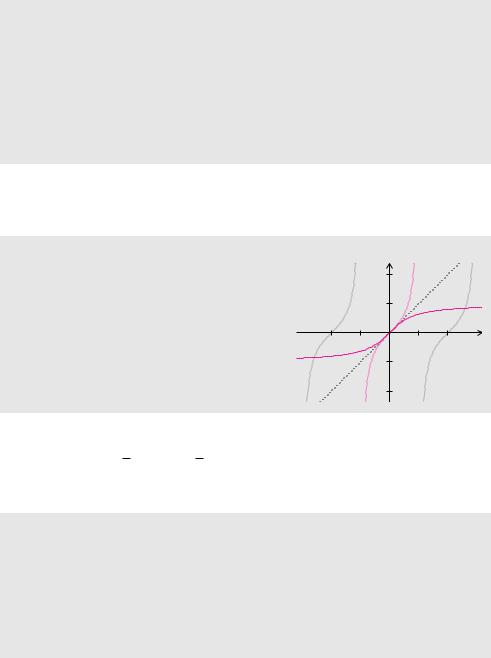
Definition 5.57 (Arkustangens und Arkuskotangens)
Die Umkehrfunktion des Tangens auf dem Intervall (−π2 , π2 ) nennt man Arkustangens:
f(x) = tan x f−1(x) = arctan x.
Entsprechend bezeichnet man die Umkehrfunktion des Kotangens auf dem Intervall
(0, π) als Arkuskotangens:
f(x) = cot x f−1(x) = arccot x.
Wir betrachten nun zunächst den Arkustangens etwas genauer. Bei der Behandlung der komplexen Zahlen in Kapitel 11 werden wir sehen, dass der Arkustangens eine wichtige Funktion zur Bestimmung des Winkels einer komplexen Zahl darstellt.
Eigenschaften des Arkustangens
LDefinitionsbereich: D = R
LWertebereich: W = (−π2 , π2 )
LSymmetrie: zum Ursprung
LMonotonie: streng monoton wachsend
LNullstelle: x = 0
|
|
y |
tan x |
|
|
|
|
π |
|
||
|
|
|
|
|
|
|
|
π |
|
arctan x |
|
|
|
2 |
|
|
|
−π |
− |
π |
π |
π |
x |
2 |
2 |
|
|||
|
|
− π2 |
|
|
|
|
|
−π |
|
|
|
Beispiel 5.72 (Werte des Arkustangens)
a) Es ist arctan (1) = π , denn tan ‹ π • = 1.
44
b) Es ist arctan (100) ≈ |
π |
, denn der Tangens strebt gegen ∞ für x gegen |
π |
|
|
|
|
. |
Ì |
||
2 |
2 |
||||
Gleichungen lösen mit Arkustangens
Der Tangens ist auf der vollen Periode umkehrbar. Alle Lösungen der Gleichung
tan x = y
ergeben sich wegen der Periode π zu
x = arctan y + k π, k Z.
