Файловый архив студентов. Файловый архив студентов.
1260 вузов, 4599 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Koch_Mathematik fur das Ingenieurstudium.pdf
Скачиваний:
107
Добавлен:
21.02.2016
Размер:
17.74 Mб
Скачать
☆
►Содержание►

9.5 Bogenlänge

377

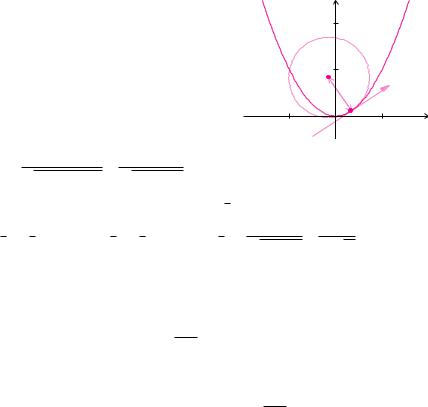
Beispiel 9.12 (Krümmungskreis einer ebenen Kurve)

Die Parameterdarstellung

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

c(t) = Œ

t

‘ ,

 

t R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

t2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

stellt die Normalparabel

als

parametrisierte

ebene

 

 

 

 

 

 

 

 

 

Kurve dar. Zur Berechnung der Krümmung benöti-

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

M

 

gen wir die beiden Ableitungen

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r

 

c′(t) = Œ

1

‘ ,

 

c′′(t) = Œ

0

‘ .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 t

 

2

 

 

 

 

 

 

 

 

−1

 

 

1

x

Daraus erhalten wir die Krümmung

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

κ(t) = ¼1122 −

0

2t

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 t 2 3 = ¼

 

1 4 t2 3

.

 

1

 

 

 

 

 

 

 

 

Beispielsweise

erhalten wir für den Parameterwert t

 

 

 

 

 

 

 

 

 

 

 

(

+ (

 

) )

 

(

 

+

 

)

 

 

=13

 

 

 

 

 

 

 

 

1

 

1

3

‘ ,

 

 

1

 

1

3

‘

 

 

1

2

94

 

 

=

54

 

c‹ 3 • =

9 Œ

1

 

c′ ‹ 3 • =

3 Œ

2

,

κ ‹ 3

• = ¼

+

Ž

3

13 √13 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

‰

 

 

 

 

 

 

Die Koordinaten des Krümmungskreismittelpunktes M zum Parameterwert t

=

 

1

ergeben sich

3

aus dem Einheitsvektor n

 

 

1

 

 

, der senkrecht auf dem Tangentenvektor steht

 

 

 

 

‹

 

3 •

 

 

 

 

 

 

c′

 

1

 

1

 

 

3

 

 

 

 

 

n

1

 

1

 

 

2

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

3

 

 

2

 

 

 

 

 

 

 

 

 

3

 

13

 

−3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

‹

 

 

• =

 

Œ

1

 

‘ Ô

 

 

 

‹

 

• =

√

 

 

Œ

 

 

‘

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Den Ortsvektor m‹

 

 

• des Krümmungskreismittelpunktes M erhalten wir aus

 

 

 

 

 

3

 

 

 

 

 

m

1

 

c

1

 

 

 

 

 

1

 

n

1

1

1

 

 

13

√

 

 

1

 

 

3

 

1

45 .

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

3

 

 

13

 

−

2

 

Œ −

8

 

 

 

‹

 

• = ‹

 

 

• +

 

 

 

 

 

 

‹

 

 

• =

 

Œ ‘ +

 

 

 

 

 

 

√

 

Œ

‘ =

 

‘

Ì

 

 

3

 

3

 

3

 

 

3

9

 

 

54

 

 

54

 

 

 

κ

 

 

 

 

 

 

 

13

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

‹

 

 

•

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Auch für Raumkurven kann man Krümmungskreise definieren. Allerdings benötigt man dazu Begri e aus der Di erenzialgeometrie wie beispielsweise die Schmiegebene oder das begleitende Dreibein, die weit über unsere einfachen Betrachtungen von Kurven hinausführen. Eine komplette Einführung in die Di erenzialgeometrie findet man beispielsweise bei [DoCarmo].

9.5 Bogenlänge

Unter der Bogenlänge einer Kurve versteht man die tatsächliche Länge einer ebenen oder räumlichen Kurve. Durchläuft man eine Kurve mit konstanter Geschwindigkeit, dann wird die Durchlaufzeit durch die Bogenlänge der Kurve bestimmt. Nähert man eine Kurve durch viele kleine Strecken an, dann bekommt man aus der Summe der einzelnen Längen dieser Strecken einen guten Näherungswert für die Bogenlänge. Konsequenterweise definiert man die Bogenlänge als Grenzwert dieser Summen, also als Integral.

378

9 Kurven

Definition 9.13 (Bogenlänge)

 

 

Die Bogenlänge einer Kurve mit der Parame-

terdarstellung c t über dem Intervall I

a, b

 

ist definiert

durch

= [ ]

( )

L = Sa b Sc′(t)S dt.

 

 

Man integriert die Länge des Tangentenvektors

über das komplette Parameterintervall.

 

O

 

(

a

)

c

 

 

 

 

 

 

L

c(b)

Zur Herleitung der Formel aus Definition 9.13 betrachten wir ein kleines Kurvenstück zwischen den Kurvenpunkten, die zu den beiden Parameterwerten t0 und t0 + t gehören. Die Länge dieses Teilbogens können wir durch die geradlinige Verbindung der beiden Punkte annähern. Für die Länge dieser Teilstrecke gilt nach Definition 9.8

O

L

≈ S

c

t0

+t0

t

) −

c

t0

t0

 

 

 

 

(t c

 

 

 

(t

c)S

)S

.

 

≈ S

 

 

′(

)S =

 

S

′(

 

 

 

 

)

 

 

c

(

t 0

 

 

 

 

t

 

 

 

 

 

 

t +

)

 

 

 

 

 

 

( 0

 

 

 

c

 

 

L

Die Formel für die komplette Bogenlänge ergibt sich durch Aufsummieren der Teilstrecken. Dies führt im Grenzwert zur Integration über das komplette Parameterintervall.

Satz 9.3 (Bogenlänge und Koordinatenfunktionen)

Für die Bogenlänge einer ebenen Kurve mit den Koordinatenfunktionen x(t) und y(t) bzw. einer Raumkurve mit den Koordinatenfunktionen x(t), y(t) und z(t) über dem Intervall I = [a, b] gelten die Formeln

L = Sa b »

 

dt,

L = Sa b »

 

dt.

x′(t)2 + y′(t)2

x′(t)2 + y′(t)2 + z′(t)2

Eine Kurve kann etwa bezüglich der Zeit parametrisiert werden. Dann entspricht der Kurvenparameter gerade der Zeit. Eine andere Möglichkeit ist die Parametrisierung der Kurve nach der Bogenlänge. Diese Variante hat die spezielle Eigenschaft, dass der Tangentenvektor stets die Länge 1 besitzt. Eine Kurve in Bogenlängenparametrisierung kann somit keine singulären Punkte enthalten. Bei der Parametrisierung nach der Bogenlänge verwendet man für die Ableitungen der Koordinatenfunktionen gern den Punkt anstelle des Ableitungsstrichs.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности