
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
5.4 Sinus, Kosinus und Tangens |
191 |
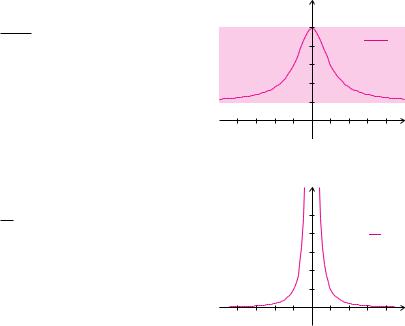
Beispiel 5.44 (Beschränkte Funktion)
Die Funktion
4
f(x) = 1 + x2 + 1
ist für alle reellen Zahlen definiert. Sie ist beschränkt. Die Funktionswerte sind alle größer als 1. Somit ist 1 eine untere Schranke. Der maximale Funktionswert ist f(0) = 5. Dadurch ist 5 eine obere Schranke. Alle Zahlenwerte kleiner 1 sind auch untere Schranken und alle Zahlen größer 5 sind auch obere Schranken.
y |
|
|
|
|
5 |
|
4 2 +1 |
|
|
4 |
f (x) = |
|
||
|
1+x |
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
−4 −3 −2 −1 |
1 2 3 4 |
x |
Ì |
|
|
|
|
|
|
Beispiel 5.45 (Unbeschränkte Funktion)
Die Funktion
f(x) =
1
x2
ist für alle reellen Zahlen außer x = 0 definiert. Die Funktionswerte sind alle größer als 0. Somit ist 0 eine untere Schranke. Auf den Intervallen I1 = (−∞, 0) und I2 = (0, ∞) ist die Funktion nicht nach oben beschränkt. Somit ist die Funktion auf diesen Intervallen auch nicht beschränkt.
y |
|
|
|
|
5 |
|
|
|
|
4 |
f(x) = |
12 |
|
|
|
|
x |
|
|
3 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
−4 −3 −2 −1 |
1 2 3 4 |
x |
Ì |
|
|
|
|
|
|
5.4 Sinus, Kosinus und Tangens
Schallwellen, elektromagnetische Wellen, Bahnkurven von Planeten und Satelliten und vieles mehr werden mathematisch durch Sinus und Kosinus beschrieben. Diese Funktionen sind also grundlegend für das Verständnis vieler Sachverhalte in den Naturwissenschaften und in der Technik. Sinus und Kosinus verwendet man insbesondere zur Beschreibung periodischer Vorgänge und Schwingungen.
5.4.1 Definition am Einheitskreis
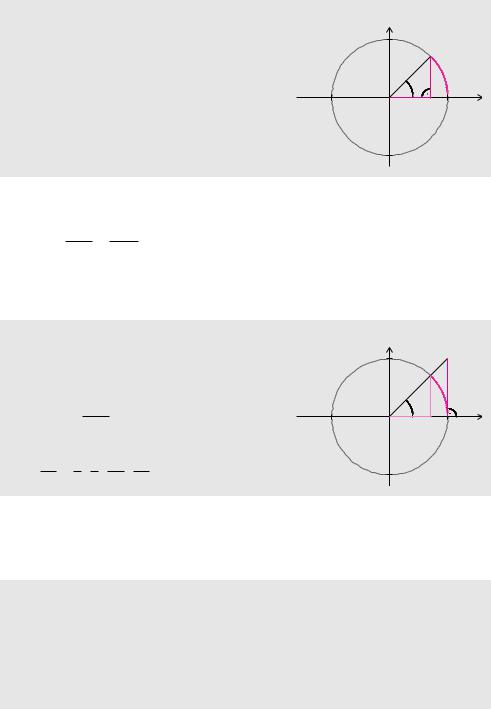
In Abschnitt 1.4 haben wir Sinus und Kosinus für Winkel im rechtwinkligen Dreieck definiert. Diese Definition kann man als Grundlage für die Definition der Sinusund Kosinusfunktion verwenden. Um Sinus und Kosinus als Funktion beliebiger reeller Zahlen zu definieren, betrachtet man Sinus und Kosinus in Abhängigkeit von der Bogenlänge. Die Bogenlänge ist dabei nicht auf einen Bereich zwischen 0 und 2 π eingeschränkt. Wir lassen beliebig viele Umdrehungen des Einheitskreises zu. Wobei wir Drehungen im mathematisch positiven Sinn, also entgegen dem Uhrzeigersinn, eine positive und Drehungen im mathematisch negativen Sinn eine negative Bogenlänge zuordnen. Somit durchläuft die Bogenlänge den kompletten Bereich der reellen Zahlen.
192 |
5 Funktionen |
Definition 5.25 (Sinus und Kosinus)
Wir betrachten den Punkt P auf dem Einheits- |
|
1 |
|
kreis und auf einer Geraden, die um den Winkel |
|
|
P |
α gegen die x-Achse gedreht ist. Der Kosinus |
|
|
x |
des Winkels α ist die x-Koordinate des Punktes |
|
α |
xsin |
P , der Sinus des Winkels α ist die y-Koordinate |
|
cos x |
|
des Punktes P . Die Funktionen Sinus und Ko- |
−1 |
1 |
|
sinus ordnen jedem Winkel x im Bogenmaß aus |
|
|
|
der Menge der reellen Zahlen den entsprechen- |
|
|
|
den Sinusund Kosinuswert zu. |
|
−1 |
|
Das Steigungsdreieck aus sin x und cos x lässt sich durch zwei verschiedene Verhältnisse ausdrücken:
m = sin x = tan x = tan x.
cos x |
1 |
Diese Beziehung erhält man auch aus dem Strahlensatz. Der Strahlenstaz beschreibt Streckenverhältnisse und wurde bereits in der Antike von Thales formuliert.
Definition 5.26 (Tangens) |
|
|
|
|
||||
Die Funktion Tangens ordnet einem Winkel x |
|
1 |
|
|
||||
im Bogenmaß das Verhältnis aus Sinus und Ko- |
|
|
x |
tan |
||||
sinus zu: |
|
|
|
|
|
|
||
|
|
|
|
|
|
xsin |
||
|
|
sin x |
|
|
α |
x |
||
tan x = cos x. |
|
−1 |
cos x |
|
1 |
|||
Der Tangens ist für alle reellen Zahlen außer |
|
|
|
|
||||
3 π |
π |
π |
3 π |
5 π |
|
|
|
|
. . . , − 2 |
, − 2 |
, 2 , |
2 , |
2 , . . . definiert. |
|
−1 |
|
|
Der Kotangens wird oft bei technischen Anwendungen verwendet. Aus mathematischer Sicht ist diese Funktion jedoch nicht besonders interessant, da es sich beim Kotangens lediglich um den Kehrwert des Tangens handelt.
Definition 5.27 (Kotangens)
Die Funktion Kotangens ordnet einem Winkel x im Bogenmaß das Verhältnis aus Kosinus und Sinus zu:
1 |
|
cos x |
|||
cot x = |
|
= |
|
|
. |
tan x |
sin x |
||||
Der Kotangens ist für alle reellen Zahlen außer . . ., −2 π, −π, 0, π, 2 π, 3 π, . . . definiert.
5.4 Sinus, Kosinus und Tangens |
193 |
5.4.2 Eigenschaften
Die meisten Eigenschaften der trigonometrischen Funktionen lassen sich direkt aus der Definition am Einheitskreis herleiten. In diesem Abschnitt fassen wir die wichtigsten Eigenschaften von Sinus, Kosinus, Tangens und Kotangens zusammen.
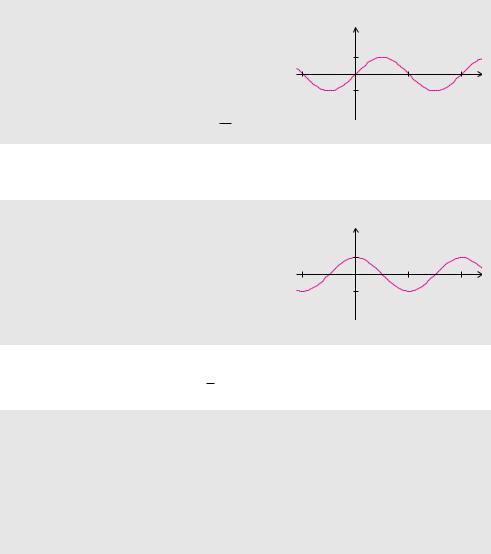
Eigenschaften des Sinus
LBereiche: D = R, W = [−1, 1]
LPeriode: p = 2 π, Symmetrie: ungerade
LNullstellen: x = k π
LExtremstellen: xH = π2 + 2kπ, xT = 32π + 2 k π
|
y |
|
|
|
1 |
sin x |
|
|
|
|
|
− π |
1 |
π |
2π x |
|
− |
|
|
Die Eigenschaften des Kosinus sind sehr ähnlich zu denen des Sinus. Am au älligsten ist der Unterschied im Symmetrieverhalten.
Eigenschaften des Kosinus
LBereiche: D = R, W = [−1, 1]
LPeriode: p = 2 π, Symmetrie: gerade
LNullstellen: x = π2 + k π
LExtremstellen: xH = 2kπ, xT = π+2kπ
|
y |
|
|
|
1 |
|
cos x |
|
|
|
|
− π |
1 |
π |
2π x |
|
− |
|
|
Sinus und Kosinus lassen sich durch geeignete Verschiebungen ineinander überführen. Man
sagt, der Sinus eilt dem Kosinus um π nach.
2
Satz 5.10 (Verschiebung von Sinus und Kosinus)
Für jede beliebige reelle Zahl x gelten folgende Formeln:
L |
sin |
‰π |
+ x Ž |
= |
sin x |
L |
cos |
‰π |
+ x Ž |
= |
−cos x |
||
L |
sin |
x |
− |
π2 |
= |
cos x |
L |
cos |
x |
− |
π2 |
= |
sin x |
sin |
(x |
π) |
sin x |
cos |
(x |
π) |
−cos x |
||||||
L |
sin |
(π2 |
+ x) |
= |
−cos x |
L |
cos |
(π2 |
+ x) |
= |
− sin x |
||
L |
|
‰ |
− |
Ž |
= |
|
L |
|
‰ |
− |
Ž |
= |
|
Die Additionstheoreme geben Auskunft darüber, wie man den Sinus und Kosinus der Summe oder Di erenz zweier Winkel mithilfe der einzelnen Sinusund Kosinuswerte berechnet. Der Nachweis der Formel erfolgt recht elegant mithilfe der Multiplikation zweier Rotationsmatrizen, siehe Abschnitt 4.8.1.

194 |
5 Funktionen |
Satz 5.11 (Additionstheoreme für Sinus und Kosinus)
Für beliebige reelle Zahlen x und y gelten die Additionstheoreme:
Lsin (x ± y)
Lcos (x ± y)
=sin x cos y ± cos x sin y
=cos x cos y sin x sin y
Setzt man in den Additionstheoremen y = x, so ergeben sich die Doppelwinkelformeln, die beschreiben, wie der Sinus oder Kosinus des doppelten Winkels aufgelöst werden kann.
Satz 5.12 (Doppelwinkelformeln für Sinus und Kosinus)
Für jede beliebige reelle Zahl x gelten die Doppelwinkelformeln:
L |
sin |
2 x |
= |
2 sin x cos x |
||
cos |
(2 x) |
cos2 x |
− |
sin2 x |
||
L |
|
( ) |
= |
|
|
|
Die Schreibweise mit dem Quadrat direkt bei Sinus und Kosinus ist in der Mathematik üblich. Die Kurzschreibweise für sin2 x = (sin x)2 und cos2 x = (cos x)2 sollte man auf keinen Fall mit sin x2 = sin ‰x2Ž und cos x2 = cos ‰x2Ž verwechseln.
Eigenschaften des Tangens
LDefinitionsbereich: x ≠ π2 + k π
LWertebereich: W = R
LPeriode: p = π
LSymmetrie: ungerade
LNullstellen: x = k π
|
y |
|
|
|
|
1 |
tan x |
|
|
|
|
|
|
|
− π |
−1 |
π |
2π |
x |
|
Wie schon beim Sinus und Kosinus stellt man bei Tangens und Kotangens eine Ähnlichkeit bei den Eigenschaften fest.
Eigenschaften des Kotangens
LDefinitionsbereich: x ≠ k π
LWertebereich: W = R
LPeriode: p = π
LSymmetrie: ungerade
LNullstellen: x = π2 + k π
|
y |
|
|
|
|
1 |
cot x |
|
|
|
|
|
|
|
− π |
−1 |
π |
2π |
x |
|

5.4 Sinus, Kosinus und Tangens |
195 |
Aus den Additionstheoremen für den Sinus und Kosinus ergeben sich direkt die Additionstheoreme für den Tangens, denn
|
|
|
|
|
|
sin |
x |
y |
|
sin x cos y |
cos x sin y |
|
tan x tan y |
|||
tan |
( |
x |
± |
y |
) = |
cos |
(x |
± y) |
= |
cos x cos y |
± sin x sin y |
= |
1 |
|
tan±x tan y |
. |
|
|
|
|
( ± ) |
|
|
|
|
|
|||||||
Bei der letzten Umformung haben wir den Bruch im Zähler und im Nenner durch den Faktor cos x cos y geteilt. Ganz analog ergeben sich direkt die Additionstheoreme für den Kotangens, denn
cot (x ± y) = cos (x ± y) = cos x cos y sin x sin y = cot x cot y 1.
sin |
x |
y |
|
sin x cos y cos x sin y |
cot y cot x |
Diesmal haben wir den( |
Bruch im Zähler und im Nenner durch den Faktor sin x sin y |
||||
± |
|
) |
± |
± |
|
geteilt.
Satz 5.13 (Additionstheoreme für Tangens und Kotangens)
Für beliebige reelle Zahlen x und y gelten die Additionstheoreme
|
|
|
|
|
|
|
x tan y |
|
|
|
|
|
|
|
cot x cot y 1 |
||
L |
tan |
( |
x |
± |
y |
) = |
1tantan±x tan y |
L |
cot |
( |
x |
± |
y |
) = |
cot y |
± |
cot x |
|
|
|
|
|
|
|
|
|
|||||||||
sofern die Nenner nicht null sind.
5.4.3 Allgemeine Sinusund Kosinusfunktion
In der Technik werden sogenannte allgemeine Sinusund Kosinusfunktionen zur Beschreibung von Schwingungen verwendet. Wir konzentrieren uns hier auf allgemeine Kosinusfunktionen. Allgemeine Sinusfunktionen lassen sich durch eine entsprechende Verschiebung in allgemeine Kosinusfunktionen überführen, siehe Satz 5.10 und Beispiel 5.46. Deshalb verzichten wir auf eine detaillierte Untersuchung allgemeiner Sinusfunktionen. Die allgemeine Sinusbzw. Kosinusfunktion wird auch als harmonische Schwingung bezeichnet.
Eine allgemeine Kosinusfunktion besteht aus einer skalierten und verschobenen StandardKosinusfunktion. Eine Skalierung der Funktionswerte bezeichnet man als Amplitude. Wir betrachten nur positive Amplituden A > 0. Eine Skalierung der unabhängigen Variablen erfolgt mithilfe einer Kreisfrequenz ω > 0. Eine allgemeine Kosinusfunktion enthält außerdem einen sogenannten Phasenwinkel ϕ. Dieser Phasenwinkel bewirkt eine Verschiebung des Schaubildes der Funktion in Richtung der Achse der unabhängigen Variablen.
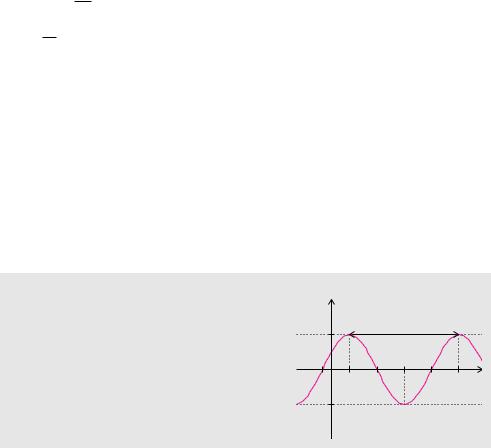
Definition 5.28 (Allgemeine Kosinusfunktion)
Eine allgemeine Kosinusfunktion wird durch
f(t) = A cos (ω t + ϕ)
beschrieben. Dabei bezeichnet A > 0 die Amplitude, ω > 0 die Kreisfrequenz und ϕ den Phasenwinkel oder die Phasenverschiebung.
196 |
5 Funktionen |
Häufig bezeichnet die unabhängige Variable der allgemeinen Kosinusfunktion der Zeit. Deshalb verwenden wir die Bezeichnung t mit der physikalischen Einheit Sekunde. Entsprechend besitzt die Kreisfrequenz ω die Einheit 1s . Dadurch ergibt das Produkt aus Zeit und Kreisfrequenz eine Größe, die wir als Wert im Bogenmaß interpretieren.
Der Verlauf einer allgemeinen Kosinusfunktion hängt von den Parametern A, ω und ϕ ab. Wir werden nun im Detail klären, welche Auswirkungen diese Parameter im Einzelnen haben. Die Amplitude A bewirkt lediglich eine Skalierung in Richtung der y-Achse. Sie hat keine Auswirkung auf die Periode der allgemeinen Kosinusfunktion. Wegen
f ‹t + 2 π • = A cos (ω t + 2 π + ϕ) = A cos (ω t + ϕ)
ω
ist T = 2ωπ die kleinste positive Periode, die man auch als Schwingungsdauer bezeichnet. Insbesondere der Begri Phasenverschiebung sorgt immer wieder für Verwirrung. Der Phasenwinkel ϕ bewirkt zwar eine Verschiebung des Schaubildes in Richtung der t-Achse, aber nicht um den Wert ϕ. Den tatsächlichen Wert t0 der Verschiebung des Schaubildes erhalten wir, wenn wir folgende beiden Darstellungen der allgemeinen Kosinusfunktion miteinander vergleichen:
A cos (ω t + ϕ) = A cos (ω (t − t0)) Ô ϕ = − ω t0 .
Es ergibt sich also eine Verschiebung um t0 = −ωϕ . Diese Verschiebung liefert beim Kosinus eine Stelle, an der ein Hochpunkt vorliegt. Alle weiteren Hochpunkte liegen im Abstand von jeweils einer ganzen Periode T . Die Tiefpunkte liegen jeweils um eine halbe Periode versetzt und wiederholen sich auch im Abstand T . Zwischen einem Hochund einem Tiefpunkt liegt jeweils eine Nullstelle. Nullstelle wiederholen sich im Abstand der halben Periode.
Eigenschaften der allgemeinen Kosinusfunktion
L Periode: T = 2ωπ
L Nullstellen: t = −ωϕ + T4 + k2T
LHochpunktstellen: t = −ωϕ + k T
LTiefpunktstellen: t = −ωϕ + T2 + k T
f(t) |
|
T = 2 π |
|
|
|
|
|
A |
|
ω |
|
|
|
|
|
|
− |
ϕ |
t |
|
ω |
||
|
|
||
−A |
f(t) = A cos (ω t + ϕ) |
|
|
