
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
13.2 Komplexe Darstellung |
543 |
13.2.3 Spektrum
Der Begri Spektrum taucht in unterschiedlichen Zusammenhängen auf. Beispielsweise spricht man bei einem Regenbogen von einer Zerlegung des Lichts in Spektralfarben. In der Chemie bezeichnet das Spektrum die einzelnen Bestandteile eines Gemisches. Spektren verwendet man ganz allgemein, um Bestandteile zu beschreiben. Das Spektrum einer Fourier-Reihe macht das Schwingungsverhalten einer periodischen Funktion sichtbar.
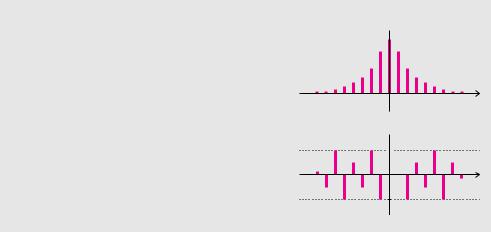
Die komplexen Fourier-Koe zienten ck lassen sich, wie alle komplexen Zahlen, nicht nur mit Realund Imaginärteil, sondern auch mithilfe der Beträge SckS und der Winkel ϕk = arg(ck), also durch ck = SckS ei ϕk , darstellen. Wie üblich betrachten wir dabei Winkel im Intervall von (−π, π]. Die Beträge und Winkel der komplexen Fourier-Koe zienten bilden das sogenannte komplexe Spektrum.
Definition 13.6 (Betragsund Phasenspektrum)
Bei der Darstellung einer Funktion f mit Periode T in Form einer komplexen Fourier-Reihe
f |
t |
∞ |
ck ei k ω t, ω |
= |
2 π |
|
|
T |
|||||
|
( |
) = kQ |
|
|
||
|
|
=−∞ |
|
|
|
|
nennt man die grafische Darstellung
Lder Beträge SckS das Betragsspektrum,
Lder Winkel arg(ck) das Phasenspektrum.
Die Darstellung erfolgt über den ganzzahligen Vielfachen der Kreisfrequenz k ω.
|ck|
k ω
arg(ck)
π 

k ω
−π
Eine Fourier-Reihe besitzt ein zweiseitiges diskretes Linienspektrum. Aus Symmetriegründen gilt Sc−kS = SckS und arg(c−k) = −arg(ck). Deshalb verzichtet man oft auf die Darstellung der Spektrallinien für negative Indizes.
Aus dem komplexen Betragsund Phasenspektrum kann man wichtige Eigenschaften der reellen Fourier-Reihe gewinnen. Dazu zerlegen wir die komplexe Fourier-Reihe
|
f |
|
t |
|
|
|
∞ |
|
ck ei k ω t |
∞ |
|
ck |
|
ei ϕk ei k ω t |
|
∞ |
ck |
ei |
k ω t ϕk |
) |
, |
||||||||||
|
|
( |
) = kQ |
|
|
|
|
= kQ S |
|
S |
|
|
|
= kQ S |
|
S |
( |
+ |
|
||||||||||||
mit ϕk |
|
|
arg |
|
|
=−∞ |
|
|
|
|
=−∞ |
|
|
|
|
|
|
|
=−∞ |
|
|
|
|
|
|
||||||
= |
( |
ck |
) |
, in Teilsummen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
k |
− |
1 |
|
|
( |
|
+ |
) |
|
|
|
|
k 1 |
|
|
( |
+ |
) |
|
|
|
|
|
|||
|
f |
|
t |
|
|
|
|
|
|
ck |
ei |
k ω t ϕk |
|
+ S |
c0 |
|
∞ |
ck |
ei |
k ω t ϕk |
|
. |
|
|
|
|
|||||
|
|
( |
) = Q S |
S |
|
|
|
|
|
S + Q S |
S |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
=−∞ |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||
Die erste Teilsumme erstreckt sich über die negativen Indizes und die zweite Teilsumme erstreckt sich über die positiven Indizes.

544 |
13 Fourier-Reihen |
Da die komplexen Fourier-Koe zienten mit negativen Indizes gerade die konjugiert komplexen Werte der Koe zienten mit positiven Indizes sind, gilt ϕ−k = −ϕk und Sc−kS = SckS. Daraus ergibt sich für die erste Teilsumme
−1
Q SckS ei(k ω t+ϕk) k=−∞
Insgesamt erhalten wir
∞
= Q Sc−kS ei((−k)ω t+ϕ−k) = k=1
∞
Q SckS e−(i k ω t+ϕk). k=1
∞
f(t) = Sc0S + Q SckS ‰ei(k ω t+ϕk)
k=1
∞
+ e−i(k ω t+ϕk)Ž = Sc0S + Q 2 SckS cos (k ω t + ϕk).
k=1 ±
Ak
Dabei haben wir die Formel zur Darstellung des Kosinus durch komplexe e-Funktionen verwendet, siehe Satz 11.2.
Darstellung mit Amplituden und Phasenwinkeln |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Die Fourier-Reihe einer Funktion f mit Periode |
Im |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
T |
= |
2 π |
lässt sich durch phasenverschobene Ko- |
|
|
|
2ck |
|||||||||||||||||||||||||||||
ω |
|
|
Ak |
|
|
|
||||||||||||||||||||||||||||||
sinusschwingungen darstellen: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
f |
t |
) = |
a0 |
∞ |
Ak cos |
( |
k ω t |
+ |
ϕk |
) |
. |
|
|
|
|
|
|
|
−ibk |
||||||||||||||
|
|
|
2 |
|
|
|
|
|
ϕkak |
|||||||||||||||||||||||||||
|
|
|
|
( |
+ kQ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aus den reellen bzw. komplexen Fourier-Koe - |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
zienten ak, bk bzw. ck kann man die |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Amplituden Ak |
|
2 |
|
ck |
|
|
¼ |
|
|
|
|
|
und |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
= |
S |
S |
= |
ak2 |
+ |
bk2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
L |
Phasenwinkel ϕk |
= |
arg |
( |
ck |
)= |
arg |
( |
ak |
− |
i bk |
) |
|
|
|
|
|
|
|
|||||||||||||||||
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
für k |
= |
1, 2, 3, . . . berechnen. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Somit gibt es zwei unterschiedliche reelle Darstellungen für Fourier-Reihen. Die FourierKoe zienten ak und bk beschreiben die Kosinusund Sinusanteile der Schwingung. Bei vielen Anwendungen hat es sich jedoch bewährt, mit Kosinus als Grundfunktion zu arbeiten und die Schwingung durch Amplituden Ak und Phasenwinkel ϕk zu beschreiben.
Eine grafische Darstellung, bei der man anstelle der Beträge SckS die Amplituden Ak verwendet, bezeichnet man als Amplitudenspektrum. Im Gegensatz zum Betragsspektrum ist das Amplitudenspektrum ein einseitiges Spektrum. Beim Betragsspektrum durchlaufen die Indizes k die Werte von −∞ bis ∞, beim Amplitudenspektrum starten die Indizes bei 0. Abgesehen davon unterscheiden sich die beiden Spektren jedoch nur um den Faktor 2.
13.2 Komplexe Darstellung |
545 |
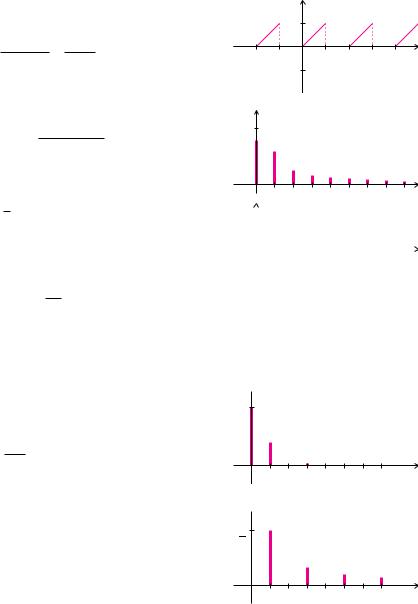
Beispiel 13.9 (Spektrum)
Die 2 π-periodische Funktion aus Beispiel 13.8 hat die komplexen Fourier-Koe zienten
|
1 |
k |
|
1 |
|
|
1 |
|
k |
|
|
|
||
ck |
= |
(−2 ) |
|
− |
|
+ |
(− |
|
) |
|
i, |
k |
= |
1, 2, 3, . . . |
|
k2 π |
|
|
2 k |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
Der Gleichanteil beträgt c0 = π4 . Somit ist Sc0S = π4 und ϕ0 = 0. Das Betragsspektrum ergibt sich zu
|
ck |
|
1 ¾ |
|
|
|
|
|
|
|
|
|
12k 2 1 |
|
2 |
|
1. |
||||
S |
|
S = |
|
|
((−k) π− |
) |
|
+ |
|
|
|
2 k |
|
|
|
||||||
Für gerade Indizes k sind die Fourier-Koe zienten rein imaginär und positiv. Somit gilt
ϕk = π für k = 2, 4, 6, . . .
2
Für ungerade Indizes k sind der Realteil und der Imaginärteil der Fourier-Koe zienten negativ. Die Phasenwinkel
ϕk = arctan ‹ k π • − π für k = 1, 3, 5, . . .
2
|
f (t) |
π |
|
−2π −π |
π 2π 3π 4π t |
−π |
|
|ck| |
|
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
k |
|||||
ϕk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π2 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
k |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
haben Werte zwischen |
− |
π und |
− |
π . Wegen ω |
= |
1 kann man die k ω-Achse auch einfach mit k |
beschriften. |
|
2 |
Ì |
Beispiel 13.10 (Amplitudenspektrum)
a)Die Fourier-Reihe der Dreieckfunktion aus Beispiel 13.6 besteht nur aus Kosinusanteilen ak. Alle Sinusanteile bk sind null. Es ist A0 = π und
Ak = k22π U(−1)k − 1U , k = 1, 2, 3, . . .
Alle Phasenwinkel ϕk sind null.
b)Die Fourier-Reihe der Rechteckfunktion aus Beispiel 13.7 besteht nur aus Sinusanteilen bk. Alle Kosinusanteile ak sind null. Es ist A0 = 0 und
2 |
|
k |
|
|
Ak = |
|
U(−1) |
|
− 1U , k = 1, 2, 3, . . . |
k π |
|
|||
Alle Phasenwinkel ϕk haben den Wert −π2 .
Ak 
π
1 2 3 4 5 6 7 k ω
Ak 
4
π
π 2π 3π 4π 5π 6π 7π |
k ω Ì |
|
546 |
13 Fourier-Reihen |
13.2.4 Minimaleigenschaft
Es stellt sich die Frage, warum man die Fourier-Koe zienten ausgerechnet mit den Formeln aus Satz 13.2 bzw. Satz 13.4 berechnet. Als Antwort wollen wir uns nicht damit begnügen, dass Fourier ein genialer Mathematiker war und schon wusste was er tut. Zur Herleitung der Formeln betrachten wir die Fourier-Reihe einer Funktion f mit Periode T in komplexer Darstellung, also
f |
t |
∞ |
ck ei k ω t, ω |
= |
|
2 π |
. |
|
|||||||
Wenn |
( |
) = kQ |
|
|
T |
||
=−∞
wir die unendliche Summe nach n Gliedern abbrechen
n
pn(t) = Q ck ei k ω t, k=−n
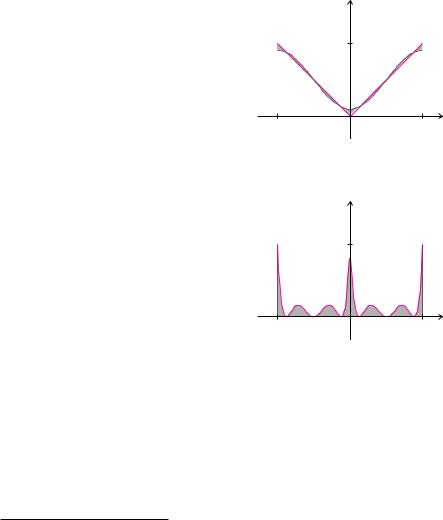
dann erhalten wir ein trigonometrisches Polynom pn vom Grad n. Zwischen der Funktion f und dem trigonometrischen Polynom pn entsteht an jeder Stelle t eine Abweichung d(t). Die FourierKoe zienten ck werden nun so bestimmt, dass diese Abweichungen insgesamt möglichst klein werden.
Wir müssen nun klären, welches mathematische Kriterium zu einer möglichst kleinen Abweichung führt. Ein guter Ansatz hierzu ist, die Abweichung d zwischen der Funktion f und dem trigonometrischen Polynom pn zu quadrieren und über die gesamte Periode T zu integrieren:
|
= |
|
T |
‰ |
|
|
|
|
) |
2dt. |
d |
|
2 |
f |
t |
pn |
t |
||||
|
S |
− T2 |
|
( |
)d−t |
( |
Ž |
|||
|
|
|
|
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|
|||||
( )
|
f(t) |
|
|
π |
|
|
pn(t) |
|
−π |
π |
t |
|
d(t) |
|
|
0.1 |
|
−π |
π |
t |
|
Damit hängt die Gesamtabweichung d nun nicht mehr von t, sondern nur noch von den Fourier-Koe zienten ab:
d = d(c−n, . . . , c−1, c0, c1, . . . , cn).
Die Fourier-Koe zienten werden so bestimmt, dass diese Gesamtabweichung d minimal wird. An einer Stelle, an der der Gesamtfehler ein Minimum hat, müssen notwendigerweise die partiellen Ableitungen von d nach allen Fourier-Koe zienten null werden:
∂d(c−n, . . . , c−1, c0, c1, . . . , cn) = 0, ` = 0, ±1, ±2, . . . , ±n.
∂c`

13.2 Komplexe Darstellung |
547 |
Die Berechnung der partiellen Ableitungen ist einfacher, als dies auf den ersten Blick scheint. Die Variablen c` kommen in der Summe nur in linearer Form vor. Deshalb gilt
∂d |
|
∂ |
|
|
|
T |
|
|
|
n |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= |
|
|
S− |
Π|
f |
t |
) − Q |
ck ei k ω t |
‘ |
|
dt |
|||
|
|
|
|
||||||||||||
∂c` |
∂c` |
’ |
|
2 |
|
|
k |
=− |
n |
|
|
|
“ |
||
|
|
|
|
” |
|
T |
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
n |
|
|
|
|
|
|
|
= −2 |
|
2 |
Œf(t) − kQn ck ei k ω t‘ ei ` ω tdt. |
|||||||||||
|
|
− T2 |
|||||||||||||
|
|
|
S |
|
|
|
|
=− |
|
|
|
|
|
|
|
Bei dieser Umformung haben wir Ableitung und Integration vertauscht. Der Faktor ei ` ω t steht bei c` und ist als innere Ableitung zu berücksichtigen. Durch Vertauschen von Summe und Integral erhalten wir die Gleichung
n |
|
|
|
T |
|
i |
( |
+ |
) |
|
|
= |
|
|
T |
|
|
) |
|
i ` ω t |
|
k n |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||
Q |
ck |
|
− |
2 |
e |
|
k ` |
|
ω t |
dt |
|
− |
2 |
f |
t |
e |
dt. |
||||
|
S |
|
|
|
|
|
|
|
|
S |
|
|
( |
|
|
|
|||||
=− |
|
|
T |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sofern k ≠ −` ist, können wir das Integral auf der linken Seite mithilfe einer Stammfunktion berechnen:
|
T |
ei k ` ω tdt |
|
|
|
e ( + ) |
|
T |
|
|
|
|
e ( + ) |
ω T |
− |
e− ( + ) |
ω T |
|
||||||||||||||
|
T |
|
|
|
|
i k ` ω t 2 |
|
|
|
|
i k ` |
|
|
|
i k ` |
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|||||||||||||||
S− |
|
( + ) |
= |
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
i k ` ω |
|
2 |
|
|
|
|
i k |
` ω |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
i k ` π |
|
|
i k= |
` π |
2 |
( |
|
+ ) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
e( |
+ ) |
|
e |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
( |
+ ) |
|
|
− ( |
+ ) |
|
|
sin |
|
|
k |
|
` |
|
π |
|
|
|
0. |
|||||||||
|
|
|
= |
|
|
|
i |
|
k |
− |
− |
|
ω |
|
|
|
= |
|
(( |
+ |
) |
) |
= |
|
||||||||
|
|
|
|
|
|
|
` |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
( |
|
+ |
) |
|
|
|
|
|
|
( |
k |
+ ) |
ω |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
` |
|
|
|
|
|
||||
Im Fall k = −` ergibt sich
TT
2 |
2 |
1 dt = T. |
S− T2 |
ei (k+`)ω tdt = S− T2 |
Somit fallen in obiger Gleichung mit der Summe auf der linken Seite alle Summenglieder bis auf k = −` weg, und es ergibt sich
c−` T = |
T |
f(t) ei ` ω tdt. |
2 |
||
− T2 |
||
|
S |
|
Schließlich können wir −` durch k ersetzen und erhalten die gesuchte Formel:
T
ck = 1 2 f(t) e−i k ω tdt.
Die partiellen Ableitungen null zu setzen, ist in der Regel nur ein notwendiges Kriterium für ein Minimum. In unserem Fall ist es jedoch auch eine hinreichende Bedingung, denn in der Gesamtabweichung kommen die Fourier-Koe zienten ck lediglich quadratisch vor. Die Gesamtabweichung ist niemals negativ und kann bei ungeschickter Wahl der FourierKoe zienten beliebig groß werden. Somit handelt es sich bei dem Extremwert sicherlich um ein Minimum.
