
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
10.3 |
Di erenziation |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
399 |
|||||||
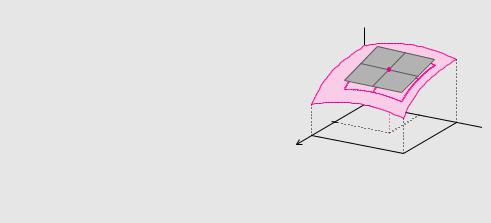
Die |
Tangentialebene der Fläche f |
( |
x, y |
) |
im Punkt |
( |
x |
0 S |
y |
0 S |
f |
( |
x , y |
0)) |
hat die Gleichung |
|||||||||
|
|
x |
|
x0 |
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||
|
|
’ |
y |
− y0 |
“ |
n |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
z |
− |
z |
0 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
– |
|
|
— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
” |
|
− |
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Durch Einsetzen des Normalenvektors und Ausmultiplizieren des Skalarprodukts erhalten wir die Tangentialebene zu
z = f(x0, y0) + fx(x0, y0)(x − x0) + fy(x0, y0)(y − y0).
Definition 10.9 (Tangentialebene)
Die Ebene durch den Punkt (x0 S y0 S f(x0, y0)) mit den Steigungen
fx(x0, y0), fy(x0, y0)
in Richtung x und y nennt man die Tangentialebene der Funktion f(x, y) an der Stelle (x0, y0). Sie existiert, falls fx und fy an der Stelle (x0, y0) stetig sind. Die Tangentialebene hat die Gleichung
z 
g(x, y)
f(x, y)
 y x
y x 

g(x, y) = f(x0, y0) + fx(x0, y0)(x − x0) + fy(x0, y0)(y − y0).
Beispiel 10.15 (Tangentialebene)
Die Funktion f(x, y) = x2 + y2 hat die partiellen Ableitungen
fx(x, y) = 2 x, fy(x, y) = 2y.
An der Stelle (1, 2) bestehen die Steigungen fx(1, 2) = 2 und fy(1, 2) = 4, siehe Beispiel 10.10. Somit lautet die Tangentialebene
z |
= |
5 |
+ |
2 x |
1 |
) + |
4 |
( |
y |
− |
2 |
) = |
2 x |
+ |
4y |
− |
5. |
Ì |
|
|
( − |
|
|
|
|
|
|
|
|
10.3.3 Gradient und Richtungsableitung
Wir haben uns bislang mit den partiellen Ableitungen beschäftigt und diskutiert, wann eine Funktion di erenzierbar ist. Wir haben noch nicht untersucht, ob man im Fall der Di erenzierbarkeit die Ableitung auch konkret formulieren kann. Setzt man alle partiellen Ableitungen zu einem Zeilenvektor zusammen, kommt man zur Ableitung oder zum sogenannten Gradienten einer Funktion.

400 |
10 Funktionen mit mehreren Variablen |
Definition 10.10 (Gradient)
Der Gradient einer Funktion f ist ein Zeilenvektor, der aus allen partiellen Ableitungen von f besteht:
f(x, y) = ‰fx(x, y), fy(x, y)Ž.
Manchmal schreibt man für den Gradienten auch f = grad f.
Die Schreibweise des Gradienten mit dem Nabla-Operator wird bevorzugt in physikalischen Anwendungen eingesetzt.
Beispiel 10.16 (Gradient) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Für die |
Funktion f |
|
|
|
|
|
haben wir in |
Beispiel |
|
10.13 die partiellen |
Ableitungen |
|||||||||||||
|
x, y |
|
x2 |
y2 |
||||||||||||||||||||
|
|
|
|
Gradient lautet»somit |
|
|
|
|
|
|
|
|
|
|||||||||||
berechnet. Der |
|
( |
|
|
|
) = |
|
+ |
|
’ |
|
|
|
|
|
|
|
|
“ . |
|
||||
|
f |
( |
x, y |
) = ‰ |
fx |
( |
x, y , fy |
( |
x, y |
|
|
x |
|
|
, |
|
y |
|
Ì |
|||||
|
|
|
|
» |
|
|||||||||||||||||||
|
|
x2 |
y2 |
|
x2 y2 |
|
||||||||||||||||||
|
|
|
|
|
) |
|
)Ž = ” » |
+ |
|
|
|
+ |
|
• |
|
|||||||||
Die partiellen Ableitungen fx und fy beschreiben die Steigungen der Schnittkurven parallel zur x-z-Ebene und y-z-Ebene. Nun sind aber auch Schnittkurven denkbar, die nicht parallel zu den Achsen verlaufen. So legt die erste Winkelhalbierende y = x in der x-y-Ebene ebenfalls eine Schnittrichtung fest. Ganz allgemein kann man Schnitte in Richtungen betrachten, die um einen Winkel α von der x-Achse verdreht sind. Diese Schnittfunktionen besitzen in der Regel auch Ableitungen. Diese werden Richtungsableitungen genannt.
Definition 10.11 (Richtungsableitung)
Die Richtungsableitung einer Funktion f an der Stelle (x0, y0) in Richtung
’ cos α “
r =
” sin α •
ist das Skalarprodukt aus Gradient und Richtungsvektor:
fr(x0, y0) = f(x0, y0) r.
|
z |
f(x, y) |
fr |
y
x |
r |
|
α |
||
|
Wichtig bei der Bestimmung der Richtungsableitung ist, dass die Richtung in normierter Form, also mit SrS = 1, vorliegt. Weitere Schreibweisen für die Richtungsableitung sind
∂f
fr(x0, y0) = ∂r V(x0,y0) = DrfS(x0,y0) .

10.3 Di erenziation |
|
|
|
|
|
|
401 |
||||
Man kann die Richtungsableitung auch direkt durch die Grenzwertbildung |
|||||||||||
f |
x, y |
lim |
f |
|
x, y |
hr |
f |
|
x, y |
|
|
|
(( |
|
) + h ) − |
|
( |
|
) |
|
|||
r( |
|
) = h→0 |
|
|
|
|
|||||
bestimmen. Wählt man als Richtungen den Einheitsvektor in Richtung der positiven x-Achse ex und den Einheitsvektor in Richtung der positiven y-Achse ey, so ergeben sich als Spezialfall die bekannten partiellen Ableitungen:
fex |
( |
x, y |
) = |
f |
( |
x, y |
) Π|
1 |
‘ = ‰ |
fx |
( |
x, y |
) |
, fy |
( |
x, y |
)Ž Œ |
1 |
‘ = |
fx |
( |
x, y |
) |
|||||||||||||
0 |
0 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
fey (x, y) = f(x, y) Œ 1 ‘ = ‰fx(x, y), fy(x, y)Ž Œ 1 ‘ = fy(x, y) |
||||||||||||||||||||||||||||||||||||
Beispiel 10.17 (Richtungsableitung) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Die Funktion f |
|
|
x, y |
|
|
|
» |
|
|
|
|
|
|
hat laut Beispiel 10.16 an der Stelle |
|
1, 2 |
|
|
den Gradienten |
|||||||||||||||||
( |
) 1= |
x2 |
+ |
y2 |
( |
) |
||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
f(1, 2) = Π|
√ |
|
, |
√ |
|
|
‘ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wir bestimmen die Richtungsableitung in Richtung x = y, also für den Winkel α = π4 . Der nor-
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
mierte Richtungsvektor ist r = |
√ |
|
|
Π|
1 |
‘. Die Richtungsableitung in Richtung r lautet somit |
|
|||||||||||||||||||||||
2 |
|
|
||||||||||||||||||||||||||||
fr |
|
1, 2 |
1 |
1, 2 |
1 |
|
|
|
1 |
|
1 |
|
1 |
|
1 |
|
2 |
|
1 |
3 |
|
Ì |
||||||||
|
5 |
2 |
|
|
1 |
|
10 |
|
|
|
|
10 . |
||||||||||||||||||
|
( |
|
) = |
√ |
|
( |
) |
√ |
|
Π|
|
‘ = |
√ |
|
( |
|
|
|
+ |
|
|
|
) = |
√ |
|
|
|
|||
Geometrisch hat der Gradient eine wichtige Bedeutung. Fasst man den Gradienten einer Funktion als Richtung auf, so zeigt der Gradient gerade in die Richtung des steilsten Anstiegs der Funktion an dieser Stelle. Das heißt, die Richtungsableitung in Richtung des Gradienten f = (fx, fy) ist größer als alle anderen Richtungsableitungen.
Satz 10.2 (Geometrische Bedeutung des Gradienten)
Der Gradient einer Funktion f an der Stelle (x0, y0) zeigt, als Richtung interpretiert, in die Richtung des steilsten Anstiegs der Funktion f an der Stelle (x0, y0).
Zum Nachweis von Satz 10.2 nehmen wir eine beliebige Richtung r = Œ rx ‘ und beginnen ry
trickreich mit der Gleichung
(fx ry − fy rx)2 ≥ 0 fx2 ry2 + fy2 rx2 ≥ 2 fx fy rx ry.
Diese Ungleichung können wir erweitern zu
fx2 rx2 + fx2 ry2 + fy2 rx2 + fy2 ry2 ≥ fx2 rx2 + 2 fx fy rx ry + fy2 ry2.
402 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 Funktionen mit mehreren Variablen |
|||||
In Faktoren umgeschrieben erhalten wir |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
( |
f2 |
+ |
f2 |
) ( |
r2 |
r2 |
) |
y≥ ( |
f r |
|
+ |
f r |
|
) |
2. |
|
|
|
|
|
|
||||||||
x |
y |
|
x |
+x |
x |
x |
|
y |
|
y |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Dividiert man durch r2 |
|
r2 und schreibt die Summen als Skalarprodukte, so gilt |
|||||||||||||||||||||||||||
|
|
|
2 |
|
|
f |
r |
2+ |
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
r |
|
|
|||
S |
f |
S ≥ |
S |
|
r 2 S |
|
|
|
Ô |
f |
|
|
f |
|
≥ |
f |
|
|
|
|
|
||||||||
S |
|
|
|
|
|
S |
r |
S |
|||||||||||||||||||||
|
|
S |
|
|
|
|
|
|
S S |
|
|
||||||||||||||||||
für alle Richtungen r = (rx, ry). Bei Funktionen mit mehr als zwei Variablen benutzt man zur Herleitung die sogenannte Cauchy-Schwarz-Ungleichung.
10.3.4 Di erenzial
Wir betrachten eine Funktion f x, y |
|
an der Stelle x0, y0 . Wenn sich die Variablen x |
|||||||||||||||||||||||||
und |
y |
um die Werte |
x |
und |
y ändern, wird die Veränderung des Funktionswerts durch |
||||||||||||||||||||||
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
( |
|
) |
|
|
|||||||||
|
|
f |
( |
x0, y0 |
) = |
f |
( |
x0 |
+ |
|
x, y0 |
+ |
y |
) − |
f |
( |
x0 |
, y0 |
) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
beschrieben. Für kleine Änderungen dx |
|
|
x und dy |
|
y entspricht die Veränderung |
||||||||||||||||||||||
des Funktionswerts |
|
f |
|
x, y |
|
ungefähr |
dem sogenannten totalen Di erenzial df |
|
x, y : |
||||||||||||||||||
|
|
|
( |
|
|
) |
|
= |
|
|
|
|
|
|
= |
|
( |
) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f(x, y) ≈ df(x, y).
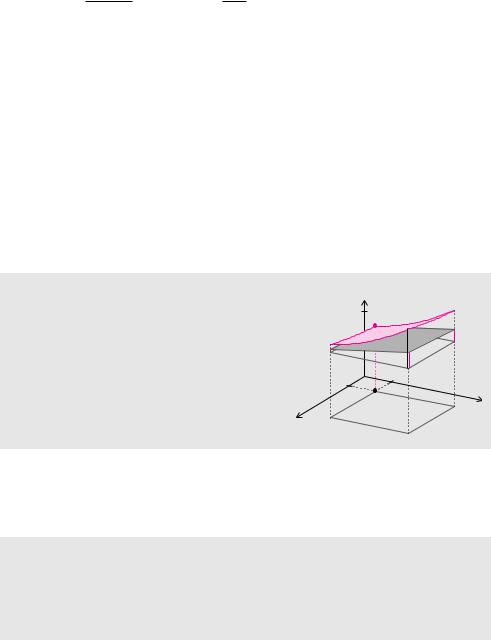
Definition 10.12 (Di erenzial)
Das totale Di erenzial einer Funktion f an der Stelle (x0, y0) ist definiert durch
dfS(x0,y0) = fx(x0, y0)dx + fy(x0, y0)dy.
Es beschreibt die Veränderung des z-Wertes an der Stelle (x0, y0) entlang der Tangentialebene, wenn sich die Variablen x und y um die Werte dx und dy ändern.
f |
z |
|
|
|
|
|
f |
fydy |
fxdx |
df |
|
|
y0 |
|
|
x0 |
y |
|
|
|
x |
|
|
|
y =dy |
x=dx |
|
|
Analog zum eindimensionalen Fall sind sowohl Schreibweisen mit dx und dy als auch mit x und y gebräuchlich. Ebenso analog zu Funktionen mit einer Variablen wird das Di erenzial zur Näherung der Änderung des Funktionswertes benutzt. Dabei ist die Genauigkeit natürlich um so besser, je kleiner die Änderungen x und y sind.
Totales Di erenzial |
( |
x0, y0 |
) |
liefert für kleine Änderungen x |
Das Di erenzial der Funktion f an der Stelle |
||||
|
|
|
und y eine gute Näherung für die tatsächliche Änderung des Funktionswerts:
dfS(x0,y0) = fx(x0, y0) x + fy(x0, y0) y ≈ f = f(x0 + x, y0 + y) − f(x0, y0).

10.3 Di erenziation |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
403 |
|||||||
Beispiel 10.18 (Totales Di erenzial) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Wir möchten eine gute Näherung des Werts c |
|
|
|
|
|
|
|
|
|
ohne Taschenrechner berechnen. |
|||||||||||||||||||||
= |
√ |
2.982 |
+ |
4.012 |
|||||||||||||||||||||||||||
Dazu schreiben wir |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
= |
√ |
|
|
|
|
|
. |
|
|
|
|||||
c |
|
3 |
|
0.02 |
|
2 |
|
4 |
|
0.01 2 |
, |
32 |
|
42 |
|
|
|
||||||||||||||
|
= ( |
|
− |
|
|
|
) |
|
+ ( |
|
+ |
|
|
) |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x, y |
|
»x |
2 |
|
y |
2 |
|
|
|
|
|
|
|||||||||||
Wir betrachten die Funktion f |
( |
) = |
|
|
|
und bilden die partiellen Ableitungen |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
+ y |
|
|
|
|
|
|
|
|||||||||
fx(x, y) = |
» |
|
, fy(x, y) = |
» |
|
. |
|
|
|
||||||||||||||||||||||
x2 + y2 |
x2 + y2 |
|
|
|
|||||||||||||||||||||||||||
Hierbei interessant ist die Stelle (x0, y0) = (3, 4). Mithilfe des Di erenzials können wir die Abweichung f vom Wert f(3, 4) = 5 durch das Di erenzial df annähern: f ≈ df = fx dx + fy dy. Mit Zahlwerten bedeutet dies
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
f ≈ |
|
(−0.02) + |
|
(0.01) = −0.004. |
|
|
|
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
|
|
= |
|
|||
Bei dieser einfachen Approximation liefert der Näherungswert c˜ |
5 |
0.004 |
4.996 also einen |
||||||||||
recht guten Näherungswert des tatsächlichen Werts |
c |
= |
4 |
.996048439 . . . |
. |
Ì |
|||||||
|
|
|
= |
− |
|
||||||||
Mithilfe des Di erenzials können einige Regeln der Di erenzialrechnung leicht hergeleitet werden. Besonders eindrucksvoll ist die Anwendung bei der sogenannten allgemeinen Kettenregel. Wir betrachten eine zusammengesetzte Funktion
g(t) = f (x(t), y(t)) .
Die beiden Funktionen x(t) und y(t) sind jeweils Funktionen von R nach R. Die Funktion f ist eine Funktion mit zwei Variablen und bildet von R2 nach R ab. Mithilfe des Di erenzials df = fx dx + fy dy folgt nach der Division durch dt
df |
|
dx |
dy |
||
|
= fx |
|
|
+ fy |
|
dt |
dt |
dt |
|||
und daraus unmittelbar
g′(t) = fx (x(t), y(t)) x′(t) + fy (x(t), y(t)) y′(t).
Man kann diese Formel sogar sehr elegant mittels des Skalarprodukts zwischen den partiellen Ableitungen fx und fy und den inneren Ableitungen x′ und y′ schreiben:
g′(t) = (fx, fy) Œ xy′′ ‘ .
Wenn das keine schöne Anwendung des Skalarprodukts ist!
Satz 10.3 (Allgemeine Kettenregel)
Die verkettete Funktion g(t) = f (x(t), y(t)) mit der Variablen t hat die Ableitung
g′(t) = fx (x(t), y(t)) x′(t) + fy (x(t), y(t)) y′(t).

404 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 Funktionen mit mehreren Variablen |
|
Beispiel 10.19 (Allgemeine Kettenregel) |
|
|
|||||||||||||||||||
Wir betrachten eine Ellipse in Parameterform |
|
||||||||||||||||||||
x t |
|
|
|
|
|
|
|
|
a cos t |
|
|
|
|
||||||||
Πy |
(t) ‘ = Œ |
|
b sin t ‘ |
|
|
|
|
||||||||||||||
mit den Halbmessern( ) |
|
a und b, siehe Definition 9.5. Der Abstand zum Ursprung |
|
||||||||||||||||||
|
» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r t |
x2 |
|
t |
|
y2 |
|
t |
|
|
|
|
||||||||||
ist von t(abhängig.) = (Nach) + |
der( )allgemeinen Kettenregel ist |
|
|||||||||||||||||||
r′(t) = |
|
|
|
|
|
x |
|
|
|
(−a sin t) + |
y |
(b cos t). |
|
||||||||
» |
|
|
|
|
|
» |
|
|
|||||||||||||
x2 |
|
|
y2 |
x2 y2 |
|
||||||||||||||||
Durch Einsetzen von x t |
|
und y t und nach Zusammenfassen der Terme erhalten wir |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
r′ t |
|
|
|
b2 |
|
|
a2( )sin t cos( t) |
|
|
|
|
||||||||||
|
( |
a2 cos2 t |
|
b2 sin2 t . |
|
|
|
||||||||||||||
( ) = |
|
|
− |
|
) |
|
|
|
|
|
|
|
|
|
|
||||||
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
In diesem Beispiel wäre mit der Form |
|
|
|
||||||||||||||||||
r(t) = √ |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|||
a2 cos2 t + b2 sin2 t |
|
|
|
|
|
||||||||||||||||
auch die direkte Berechnung der Ableitung möglich gewesen. |
Ì |
||||||||||||||||||||
Betrachten wir nun eine Funktion y(x) in einer Variablen, allerdings in impliziter Form:
F (x, y(x)) = 0.
Ist die Ableitung y′(x) gesucht, so haben wir in Abschnitt 6.2.4 die Methode des impliziten Di erenzierens kennengelernt. Mit der allgemeinen Kettenregel können wir nun eine Formel dafür herleiten:
dF = Fx 1 + Fy y′. dx
Nun soll ja F konstant null sein, also ist auch die Ableitung dF überall null. Wir lösen dx
nach y′ auf und erhalten
y′(x) = −Fx(x, y(x)). Fy(x, y(x))
Implizite Di erenziation
Beim Ableiten einer impliziten Gleichung F (x, y) = 0 in den Variablen x und y nach x erhält man y′(x) mit der allgemeinen Kettenregel in der Form
y′(x) = −Fx(x, y(x)). Fy(x, y(x))
