
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

6.3 Regel von Bernoulli-de l’Hospital |
265 |
Ableitungsregeln |
(C f(x))′ |
|
|
||||
Faktorregel |
|
|
|||||
Summenregel |
(f(x) ± g(x))′ |
||||||
Produktregel |
f x |
g |
( |
x |
)) |
′ |
|
|
( f( x) |
|
|
|
|||
Quotientenregel |
g |
(x) |
′ |
|
|
|
|
|
Π|
( ) ‘ |
|
|
|
|
|
Kettenregel |
(f(u(x)))′ |
|
|
||||
Umkehrfunktion |
‰f−1(y)Ž′ |
|
|
|
|||
=C f′(x)
=f′(x) ± g′(x)
=f′(x) g(x) + f(x) g′(x)
=
f′(x) g(x) − f(x) g′(x)
g(x)2
=f′(u(x)) u′(x)
1
= f′(x)
In zahlreichen Beispielen haben wir für die meisten elementaren Funktionen bereits Ableitungsfunktionen explizit hergeleitet. Die wichtigsten Ergebnisse halten wir in Form einer Tabelle fest.
|
Ableitungen der wichtigsten Funktionen |
|
|
|
|
|
|
|
|
||||||||||||||
|
Funktion f |
|
|
x |
|
Ableitung f′ |
x |
|
Funktion f |
|
x |
|
Ableitung f′ |
x |
|||||||||
|
|
a |
|
a |
|
|
( |
|
) |
|
|
a 1 |
( ) |
|
sin x |
( |
|
) |
|
cos x |
( ) |
||
|
x |
( |
|
R |
) |
|
a x − |
|
|
|
|
|
− |
|
|||||||||
|
e |
x |
|
|
|
|
ex |
|
|
cos x |
|
|
|
sin x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|||
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
arctan x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
1 + x2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.3 Regel von Bernoulli-de l’Hospital
Ableitungen sind durch Grenzwerte definiert. Umgekehrt kann man Grenzwerte auch mithilfe von Ableitungen berechnen. Diesen Sachverhalt hat der Schweizer Mathematiker
Johann Bernoulli erkannt. Der französische Mathematiker Guillaume François Antoine Marquis de l’Hospital hat ihm diese Idee abgekauft und unter seinem Namen verö entlicht. Ein Verfahren zur Berechnung von Grenzwerten ist heute unter dem Namen dieser beiden Mathematiker bekannt.
Bisher haben wir einige Grenzwerte durch Plausibilitätsbetrachtungen oder mithilfe von Computern näherungsweise bestimmt. Mithilfe der Regel von Bernoulli-de l’Hospital sind wir nun in der Lage, diese Grenzwerte mathematisch exakt zu berechnen.
266 |
6 Di erenzialrechnung |
Die Regel von Bernoulli-de l’Hospital lässt sich nur auf bestimmte Typen von Grenzwerten anwenden. Es werden nur Grenzwerte in Form von Quotienten betrachtet, bei denen sowohl der Zähler als auch der Nenner gegen null streben oder bei denen sowohl Zähler als auch Nenner gegen ±∞ streben.
Satz 6.11 (Regel von Bernoulli-de l’Hospital)
Falls die beiden Grenzwerte |
lim f x |
und lim g x |
entweder beide gegen 0 oder |
|||||||||||||
beide gegen |
|
|
|
|
|
|
|
|
x x0 |
( ) |
x |
→ |
x0 |
( |
) |
|
±∞ |
streben, dann→gilt |
|
|
|||||||||||||
lim |
f |
|
lim |
f |
′ |
x |
, |
|
|
|
|
|
|
|||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||
x x0 |
g |
(x) |
= |
x |
→ |
x0 |
g |
|
(x) |
|
|
|
|
|
|
|
→ |
|
( ) |
|
|
|
′( ) |
|
|
|
|
|
|
|
|||
sofern der Grenzwert auf der rechten Seite als eigentlicher oder uneigentlicher Grenzwert existiert und die Funktionen f und g an der Stelle x0 di erenzierbar sind. Die Regel gilt auch für x → ±∞.
Dass die Regel von Bernoulli-de l’Hospital tatsächlich richtig ist, lässt sich plausibel erklären. Nähert man zwei Funktionen f(x) und g(x) mit f(x0) = 0 und g(x0) = 0 durch ihre Tangenten an der Stelle x0 an, dann gilt
lim |
f x |
|
lim |
f x0 |
f |
′ |
x0 |
x |
x0 |
|
lim |
f |
′ |
x0 |
. |
|||||
g |
(x) |
|
g(x0) + g |
(x0 )(x |
−x0 ) |
|
g |
|||||||||||||
x x0 |
≈ |
x |
→ |
x0 |
|
= |
x |
→ |
x0 |
|
(x0) |
|||||||||
→ |
|
( ) |
|
|
( ) + |
′( )( − ) |
|
|
|
′( ) |
||||||||||
Der Nachweis für den Fall, dass die Grenzwerte in Zähler und Nenner gegen ∞ gehen, lässt sich auf den Fall, dass beide Grenzwerte gegen null gehen, zurückführen. Auf weitere Details dazu verzichten wir jedoch hier.
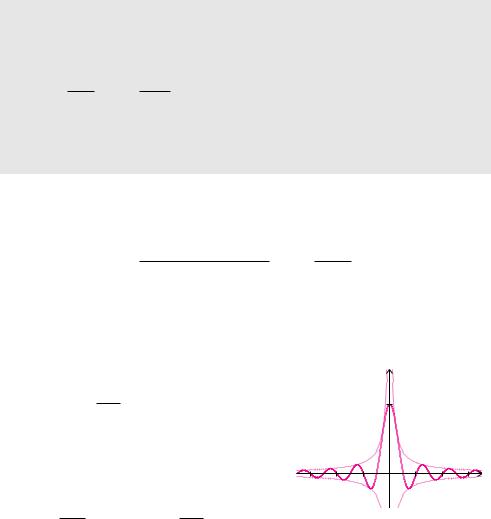
Beispiel 6.18 (sinc-Funktion) |
|
|
|
|
|
|
|
|
|
|||||
Um zu entscheiden, ob die Funktion |
|
|
|
|
y |
|
||||||||
|
¨ |
sin x |
|
|
|
≠ |
|
|
|
|
|
|
|
|
sinc x |
¨ |
|
|
für |
|
0 |
|
|
|
|
|
|
||
¢ |
|
x |
x |
|
|
|
|
|
1 |
|
||||
|
¨ |
|
1 |
für |
x |
|
0 |
|
|
|
|
f (x) = sinc x |
||
|
¨ |
|
|
|
|
|
|
|
|
|||||
|
= ¦ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¤ |
|
|
|
Grenzwert für x gegen 0. |
|
|
|
|
|||||
|
¨ |
|
|
|
|
|
|
|
||||||
stetig ist, berechnen wir den |
|
|
= |
|
|
|
|
|
|
|
||||
Die Grenzwerte im Zähler und im Nenner sind beide |
|
|
|
6π x |
||||||||||
null und der Grenzwert der Ableitungen existiert, |
−6π |
−4π |
4π |
|||||||||||
lim cos x |
= |
1 |
Ô |
|
lim sin x |
= |
1. |
|
|
|
|
|||
x→0 1 |
|
|
x→0 x |
|
|
|
|
|
||||||
Somit ist die sinc -Funktion auf ganz R stetig. |
Ì |
In Beispiel 6.18 haben wir herausgefunden, dass sich sin x für kleine x Werte genau wie x verhält. Dieser Sachverhalt wird oft in der Physik verwendet.

6.3 Regel von Bernoulli-de l’Hospital |
267 |
Verhalten des Sinus für kleine Werte
Für kleine x-Werte verhält sich sin x wie x, mit anderen Worten:
lim sin x = 1.
x→0 x
Manchmal führt die Regel von Bernoulli-de l’Hospital nicht auf Anhieb zum Ziel. In vielen Fällen wird man aber durch Hartnäckigkeit belohnt, indem man die Regel einfach wiederholt anwendet. Trotzdem darf man nicht vergessen, dass die Regel von Bernoulli-de l’Hospital kein Allheilmittel ist. Es gibt durchaus Fälle, bei denen auch die mehrfache Anwendung der Regel nicht zum Erfolg führt.
Beispiel 6.19 (Regel von Bernoulli-de l’Hospital)
Bei dem Grenzwert lim x3 gehen sowohl Zähler als auch Nenner gegen ∞. Die gleiche Situation
x→∞ ex
tritt bei den Grenzwerten der Ableitungen lim |
3 x2 |
wieder ein. Trotzdem können wir von der |
|
ex |
|||
x |
|
Regel von Bernoulli-de l’Hospital profitieren, in dem wir die Regel so oft anwenden, bis im Zähler |
||||||||||||||||||||
kein x mehr vorhanden ist: |
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
= |
|
Ô |
|
6 x |
= |
|
Ô |
|
3 x2 |
= |
|
Ô |
|
x3 |
= |
|
|
||
xlim |
|
0 |
xlim |
|
|
0 |
xlim |
|
0 |
xlim |
|
0. |
Ì |
|||||||
ex |
ex |
ex |
ex |
|||||||||||||||||
→∞ |
|
→∞ |
|
|
|
→∞ |
|
|
→∞ |
|
|
|
||||||||
Den Sachverhalt aus Beispiel 6.19 können wir auf den Zusammenhang zwischen dem asymptotischen Verhalten der e-Funktion und dem von Polynomen von beliebigem Grad verallgemeinern.
Asymptotisches Verhalten von e-Funktion und Potenzfunktionen
Für große x-Werte wächst die e-Funktion schneller als jede Potenzfunktion und somit auch schneller als jedes Polynom. Als Grenzwert formuliert:
|
n |
|
|
|
an xn |
+ |
an 1 xn−1 |
|
+ |
a2 x2 |
+ |
a1 x |
+ |
a0 |
|
|
lim |
x |
|
lim |
.x. . |
|
0, n N. |
||||||||||
x |
|
|
|
|
|
|
||||||||||
x |
e |
= |
x |
→∞ |
− |
+e |
|
|
|
= |
|
|||||
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|||||
Nach Satz 6.11 darf man die Regel von Bernoulli-de l’Hospital nur auf Quotienten anwenden, bei denen sowohl Zähler als auch Nenner gegen null streben oder bei denen sowohl Zähler als auch Nenner gegen ±∞ streben. Solche Grenzwerte bezeichnet man als
unbestimmte Ausdrücke vom Typ 0 oder ±∞. Bei anderen Typen von unbestimmten Aus-
0±∞
drücken lässt sich die Regel zwar nicht direkt, dafür aber nach geeigneten Umformungen, anwenden.

268 |
|
|
|
|
|
|
6 Di erenzialrechnung |
|
|
|
|
|
|||
Umformung unbestimmter Ausdrücke |
|
||||||
Unbestimmte Ausdrücke vom Typ |
|
|
|||||
|
|
, |
0 , 00, 1∞, |
0 |
|
||
formt∞man− ∞so um, ∞dass man einen unbestimmten∞ |
Ausdruck von folgendem Typ erhält: |
||||||
0 |
oder |
|
∞ |
. |
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
∞ |
|
|
|
Einige Umformungen sind relativ trickreich und verwenden teilweise die e-Funktion oder die ln-Funktion. Wir verzichten auf eine systematische Übersicht und erläutern das Prinzip lediglich anhand einzelner Beispiele.
Beispiel 6.20 (Unbestimmte Ausdrücke) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
a) |
Der Grenzwert lim |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
• |
ist ein unbestimmter Ausdruck vom Typ |
∞ − ∞ |
. Er lässt |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
sich durch |
|
|
|
|
x→0 ‹ x − sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
lim |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
lim |
sin x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
‹ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x→0 |
− sin x• = x→0 |
x sin−x |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
in einen unbestimmten Ausdruck vom Typ |
|
|
|
umwandeln. Der Grenzwert der Ableitungen |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
cos x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x−cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x→0 sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
ist nun wiederum ein unbestimmter Ausdruck vom Typ |
|
. Wir können jedoch versuchen, die |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Regel von Bernoulli-de l’Hospital ein zweites Mal anzuwenden. Erneutes Ableiten ergibt |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
lim |
|
|
cos x 1 |
0 |
lim |
|
1 |
|
|
1 |
|
|
|
0. |
|||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
cos x |
|
|
|
|
x sin x |
|
|
|
|
|
|
|
|
x |
|
sin x |
|
|
||||||||||||||||||||||||||||||
|
x |
→ |
0 |
cos |
|
|
|
|
|
|
|
|
|
|
x |
→ |
0 sin x x cos x |
= |
x |
→ |
0 |
|
• = |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
Ô |
|
|
|
|
|
− |
|
Ô |
|
‹ |
− |
|
|||||||||||||||||||
b) |
Der Grenzwert lim |
|
|
x ln x |
|
ist vom Typ 0 |
|
|
|
, wir können ihn aber durch |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
x |
→ |
0 |
|
− |
ln x ) |
|
|
|
|
|
|
|
|
|
|
∞ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
lim |
( |
x ln x |
) = |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
→ |
0 |
|
|
|
|
|
|
x |
→ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
in einen Grenzwert vom Typ |
umformen. Der Grenzwert der Ableitungen |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
lim |
|
|
x |
|
|
lim |
|
|
|
x |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x→0 |
|
= x→0(− ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x2
existiert und somit ist lim (x ln x) = 0. Der Logarithmus ist jedoch nur für x > 0 definiert,
x→0
deshalb handelt es sich dabei nur um einen rechtsseitigen Grenzwert.
c) Der Grenzwert lim xx ist vom Typ 00. Durch Umformung erhalten wir
x→0
lim xx |
lim eln xx |
lim ex ln x e0 1. |
|
|
||
x |
x 0 |
x 0 |
wir aufgrund= = |
|
|
|
Dabei→0ist zu= beachten,→ =dass→ |
des Logarithmus nur noch Werte x |
> |
0 betrachten |
|||
dürfen. Auch hier handelt es sich nur um einen rechtsseitigen Grenzwert. |
Ì |
|||||
