Файловый архив студентов. Файловый архив студентов.
1294 вуза, 5023 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Koch_Mathematik fur das Ingenieurstudium.pdf
Скачиваний:
113
Добавлен:
21.02.2016
Размер:
17.74 Mб
Скачать
☆
►Содержание►

160

5 Funktionen

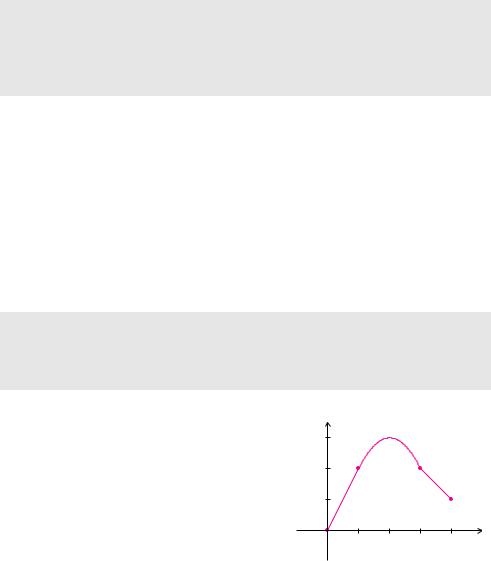
Beispiel 5.6 (Achsenschnittpunkte)

Die Funktion

f(x) = 1 x3 + 1 x2 − 1 x − 2 8 2 2

hat an der Stelle x = 0 den Funktionswert f(0) = −2. Der Schnittpunkt mit der y-Achse hat die Koordinaten (0 S − 2). Die Nullstellen der Funktion haben die x-Werte x1 = −4, x2 = −2 und x3 = 2, wie man leicht durch Einsetzen der Werte in die Funktionsgleichung bestätigen kann. Methoden zur Berechnung aller Nullstellen von Polynomen werden wir später noch kennenlernen.

y

f (x)

3

2

 

1

 

−4 −3 −2 −1

1 2 3 4 x

−1

 

−2

 

−3

 

Ì

5.1.4 Explizite und implizite Darstellung

Die Darstellung von Funktionen durch explizite Angabe einer Funktionsgleichung in der Form y = f(x) ist uns von der Schulmathematik vertraut und wurde bereits in einigen Beispielen verwendet. Es gibt jedoch noch andere Arten, Funktionen zu definieren. Bei der sogenannten impliziten Darstellung betrachtet man eine Gleichung mit den Variablen x und y. Einem x-Wert wird dabei ein y-Wert so zugeordnet, dass die Gleichung beim Einsetzen der beiden Werte erfüllt ist.

Beispiel 5.7 (Implizite Funktionsgleichung)

 

 

2

 

Die implizite Gleichung y

 

xy

 

2 kann man explizit nach y auflösen, nämlich als y

 

 

.

 

 

1

 

 

 

 

 

implizite Gleichung die Funktion

 

x

Somit definiert die

 

 

−

 

=

 

=

 

−

 

 

f(x) =

 

 

2

.

 

 

 

 

 

 

 

 

 

1

x

 

 

 

 

 

 

 

 

 

Wenn man in

der impliziten Gleichung für x den Wert 1 einsetzt, dann gibt es keinen y-Wert,

 

 

−

 

 

 

 

 

 

 

 

 

Ì

der die Gleichung erfüllt. Dies hat zur Folge, dass die Funktion für x = 1 nicht definiert ist.

 

Nicht jede implizite Gleichung definiert eine Funktion. Probleme treten auf, falls sich die Gleichung nicht eindeutig nach y auflösen lässt.

Beispiel 5.8 (Kreisgleichung)

 

 

 

 

 

 

 

Alle Punkte auf dem Einheitskreis werden durch die

y

√

 

implizite Gleichung

x2 y2

 

1 beschrieben. Diese

1

2

Gleichung kann man

nach y auflösen: y

 

1 x2.

 

1 − x

 

+

=

 

 

= ±

 

−

 

 

 

Allerdings erhält man durch die beiden

unterschiedli-

 

 

 

 

 

√

 

 

 

 

chen Vorzeichen nicht zu jedem x-Wert genau einen

 

 

 

y-Wert. Die Gleichung erzeugt zwei Funktionen. Das

−1

1

x

Schaubild der einen Funktion ist der obere Halbkreis

 

√

 

und das Schaubild der anderen Funktion ist der unte-

 

2

re Halbkreis. Der Vollkreis lässt sich nicht als Schau-

1

− 1 − x

 

bild einer einzigen Funktion darstellen.

 

 

 

 

−

 

Ì

 

 

 

 

 

 

5.1 Einführung

161

Neben dem Problem der Eindeutigkeit treten bei impliziten Gleichungen noch weitere Probleme auf. So kann es durchaus sein, dass eine Gleichung überhaupt keine Lösungen besitzt und somit auch keine Funktion definiert wird.

Beispiel 5.9 (Implizite Funktionsgleichung ohne Lösung)

Es gibt keine reellen Zahlen, für die die Gleichung

 

x2

y2

 

1

 

Diese Gleichung definiert also keine Funktion.

Ì

erfüllt ist. +

 

= −

 

Implizite Funktionsgleichung

Funktionen kann man auch durch implizite Gleichungen definieren. Dabei ist jedoch zu beachten, dass nicht jede implizite Gleichung eine eindeutige Funktion definiert. Unter Umständen werden durch eine implizite Gleichung mehrere Funktionen definiert. Es gibt auch implizite Gleichungen, die gar keine Funktion definieren.

5.1.5 Abschnittsweise definierte Funktionen

In der Technik bezeichnet man die grafische Darstellung von zwei voneinander abhängigen physikalischen Größen als Kennlinie. Beispielsweise kennzeichnet der Zusammenhang zwischen Drehzahl und Drehmoment einen Motor. Bei Antrieben steigt typischerweise das Drehmoment bei niedrigen Drehzahlen linear an, bei großen Drehzahlen fällt das Drehmoment linear ab. Im mittleren Drehzahlbereich ähnelt der Verlauf einer Parabel.

Solche wechselnden Zusammenhänge sind typisch für technische Anwendungen. Mathematisch beschreibt man solche wechselnden Verläufe durch sogenannte abschnittsweise definierte Funktionen.

Definition 5.5 (Abschnittsweise definierte Funktion)

Eine Funktion, bei der der Definitionsbereich aus endlich vielen Teilintervallen besteht, auf denen jeweils eine separate Funktionsvorschrift gilt, nennt man eine abschnittsweise definierte Funktion. Die Grenzen der Teilintervalle nennt man Nahtstellen.

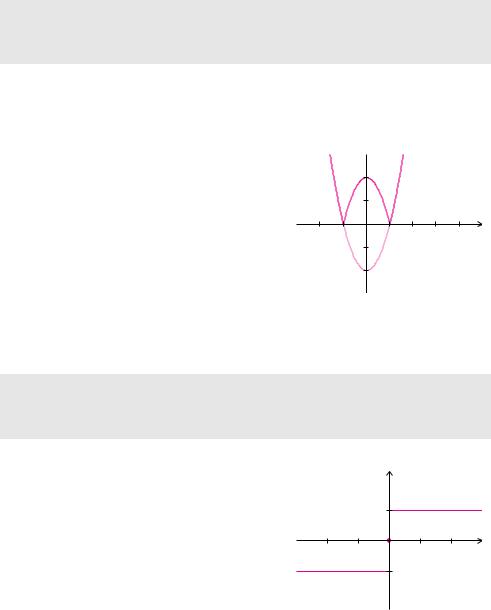
Beispiel 5.10 (Abschnittsweise definierte Funktion)

Die abschnittsweise definierte Funktion

f x

¢

3

 

x

2 2

für

1

≤

x

<

3

 

¨

2 x

 

 

für

0

x

1

 

¨

 

 

 

 

 

 

 

 

 

 

 

¨

 

 

 

 

 

 

 

 

 

 

 

¨

 

 

x

 

 

 

 

x

 

 

(

¨

5

 

− )

für

3

≤

<

4

) = ¦

− (

 

 

¨

 

 

 

 

 

 

 

 

 

 

 

¨

 

 

 

 

 

 

 

 

 

 

 

¨

 

 

 

 

 

 

 

 

 

 

 

¨

 

−

 

 

 

 

≤

 

≤

 

 

¨

 

 

 

 

 

 

 

 

¤

 

 

 

 

 

 

 

 

 

 

besitzt den Definitionsbereich D = [0, 4]. Sie besteht aus drei Abschnitten, die an den Nahtstellen x = 1 und x = 3 zusammengesetzt sind. An der Nahtstelle x = 1 besitzt das Schaubild keinen Sprung und keinen Knick. An der Nahtstelle x = 3 besitzt das Schaubild auch keinen Sprung, aber einen Knick.

y

 

 

 

 

3

 

 

 

 

2

 

 

f (x)

 

1

 

 

 

 

1

2

3

4

x

Ì

162

5 Funktionen

Abschnittsweise definierte Funktion

Bei abschnittsweise definierten Funktionen ist das Verhalten an den Nahtstellen von Interesse. An den Nahtstellen kann das Schaubild Knicke oder sogar Sprünge haben.

Methoden zum Untersuchen des Verhaltens an Nahtstellen werden wir in Abschnitt 5.5 und in Kapitel 6 kennenlernen. Ein Betragszeichen in der Funktionsgleichung erzeugt typischerweise eine abschnittsweise definierte Funktion.

Beispiel 5.11 (Betrag einer Parabel)

Die Funktion f(x) = Sx2 − 4S lässt sich durch Fallunterscheidung in der Form

 

 

 

f

x

−(

x2

−

4

)

für

x2

−

4

≥

0

 

 

 

x2

4

für

x2

4

0

 

 

 

 

( ) = œ

−

 

 

2

− <

 

darstellen. Da die Nullstellen von x

 

 

 

4 gerade bei

x

 

2

liegen, lässt sich die

Darstellung weiter ver-

 

= ±

 

 

 

 

−

 

 

 

 

 

einfachen

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f

x

 

x2

−

4

 

für x

.[−

2, 2

]

 

 

 

 

−(x2

4)

sonst

 

 

 

 

 

 

 

 

( ) = œ

 

 

−

 

 

 

 

 

 

 

 

 

 

 

y

4f (x) = |x2 − 4|

2

−4 −2

2 4 6 8

x

 

−2

x2 − 4

 

−4

 

 

Das Schaubild von f x

entsteht aus dem Schaubild der Parabel, in dem die Abschnitte mit

negativen

Funktionswerten an der x-Achse gespiegelt werden.

Ì

( )

 

Betragsfunktion

Das Schaubild der Funktion f(x) = Sg(x)S entsteht aus dem Schaubild der Funktion g(x), indem man die Punkte mit negativem y-Wert an der x-Achse spiegelt.

Beispiel 5.12 (Signumfunktion)

 

 

 

 

 

 

 

 

 

Ähnlich

wie

Betragsfunktionen

lässt

sich auch

die

 

 

y

 

 

Signumfunktion f x

 

sgn x

 

durch Fallunterschei-

 

 

f (x) = sgn(x)

dung als

abschnittsweise definierte Funktion darstel-

 

 

 

 

1

 

 

 

 

(

) =

 

(

 

)

 

 

 

 

 

 

 

 

 

len:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¨ −

1

 

für

x

<

0

 

 

 

 

 

 

 

 

 

 

 

1

 

für

x

0 .

 

 

 

1

 

 

f x

 

sgn x

¨

 

 

 

 

−2

−1

1

2

x

 

¢

 

0

 

für

x

 

0

 

 

( ) =

(

 

¨

 

 

 

 

 

=

 

 

 

 

−

 

 

 

) = ¦

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¨

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¨

 

 

 

 

 

>

 

 

 

 

 

 

 

 

 

 

 

 

¨

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¤

 

 

 

 

 

 

 

 

 

 

 

 

Ì

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

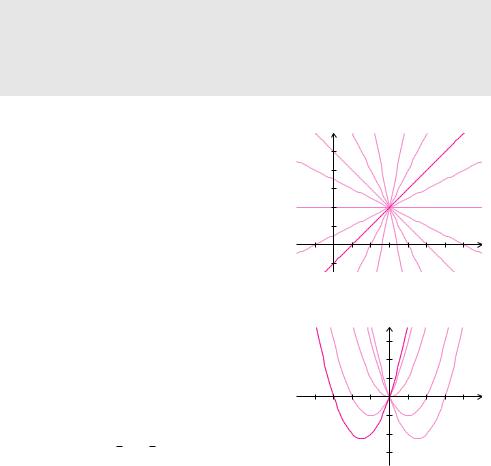
5.1.6 Funktionsschar

Oftmals treten Funktionen auf, die alle von derselben Bauart sind. Zum Beispiel Geraden, die alle unterschiedliche Steigung haben und deren Schaubilder alle durch denselben Punkt gehen. Oder Parabeln, die alle den Scheitel im selben Punkt haben.

5.1 Einführung

163

Definition 5.6 (Funktionsschar)

Eine Funktionsschar ist eine Menge verschiedener Funktionen, deren Zuordnungsvorschriften sich in einem Parameter unterscheiden. Zur Unterscheidung zwischen Variable und Scharparameter wird der Scharparameter üblicherweise als Index beim Funktionsnamen angegeben.

Beispiel 5.13 (Funktionsschar)

 

 

 

 

 

 

 

 

 

 

 

a)

Die Funktionsschar

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

fm x

m x

3

 

2

 

 

 

 

 

5

 

 

 

 

 

f1(x)

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

besteht(

aus) = allen( −Geraden,) +

 

 

 

 

 

 

 

 

 

 

 

 

die durch den festen

 

3

 

 

 

 

 

 

 

Punkt

3 2

 

gehen und eine beliebige Steigung

 

2

 

 

 

 

 

 

 

haben.(NurS

)die senkrechte Gerade x

=

3 gehört

 

1

 

 

 

 

 

 

 

nicht zur Schar. Beispielsweise ist

 

−1

 

1 2 3 4 5 6 7 x

 

f1 x x 1

 

 

 

 

 

 

 

 

 

die Gerade( ) =

 

mit−

Steigung

1

und y-Achsenab-

−1

 

 

 

 

 

 

b)

schnitt −1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Die Funktionsschar

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

a 2

a2

 

 

 

 

 

 

 

3

 

 

 

 

 

fa x

 

 

x

 

 

 

 

 

 

 

 

2

 

 

 

 

 

besteht(

)aus= (Normalparabeln.− ) −

Für jeden Wert des

 

 

 

1

 

 

 

 

 

Parameters a hat der Scheitel der Parabel die

 

 

 

 

 

 

 

 

 

Koordinaten

(

a

 

a2

 

. Beispielsweise ist

−4

−3

−2

−1

1

2

3

4 x

 

 

 

 

 

S −3 2)

9

 

 

 

 

 

 

 

−2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−1

 

 

 

 

 

f− 23 (x) = ‹x + 2 • − 4

 

 

 

 

 

f−23 (x) −3

 

 

 

 

eine Normalparabel mit Scheitel in ‹−

3

V −

9

•.

 

2

4

Ì

5.1.7 Verkettung von Funktionen

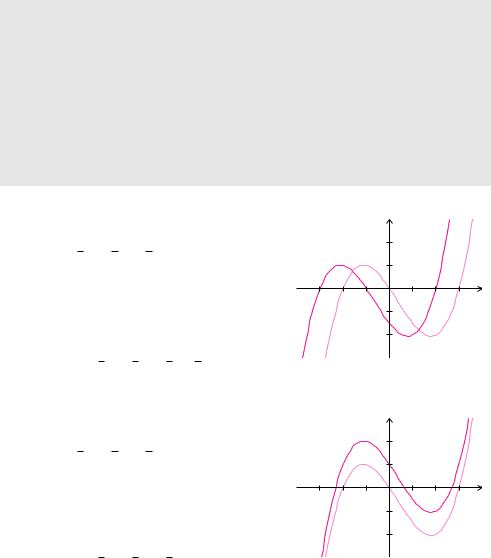
Der Funktionsbegri ist von zentraler Bedeutung in Mathematik, Naturwissenschaft und Technik. Eine wesentliche Ursache dafür ist das Baukastenprinzip. Komplizierte Funktionen entstehen durch Verkettung mehrerer einfacher Funktionen. Die einfachsten Arten von Verkettungen sind Verschiebungen und Skalierungen von Funktionen. Wir werden in diesem Abschnitt jedoch auch das allgemeine Verkettungsprinzip aufgreifen. In der Mathematik bezeichnet man dieses Prinzip als Komposition.

Auf Schaubilder von Funktionen lassen sich einfache geometrische Transformationen wie etwa Translationen oder Skalierungen anwenden. Uns beschäftigt die Frage, wie sich diese Transformationen auf die Funktionsgleichung auswirken.

164

5 Funktionen

Eine Verschiebung um den Wert x0 in x-Richtung und um y0 in y-Richtung ist im Grunde nichts anderes als eine Koordinatentransformation, bei der x durch x − x0 und y durch y − y0 ersetzt wird.

Definition 5.7 (Verschiebung, Translation)

Definiert man eine neue Funktion f˜, indem man in der Funktion f die Variable x durch x − x0 ersetzt und zu dem Funktionswert y0 addiert

f˜(x) = f(x − x0) + y0,

dann entsteht das Schaubild der neuen Funktion f˜ durch Verschieben des Schaubildes von f in Richtung der x-Achse um x0 und in Richtung der y-Achse um y0. Dabei erzeugt ein positiver x0-Wert eine Verschiebung nach rechts und ein negativer x0-Wert eine Verschiebung nach links. Ein positiver y0-Wert verschiebt nach oben und ein negativer y0-Wert nach unten.

Beispiel 5.14 (Funktion verschieben in x)

Das Schaubild der Funktion

 

 

 

 

 

 

 

y

 

 

 

 

1

3

−

1

 

2

−

3

 

 

 

 

 

 

2

 

˜

 

 

 

 

 

 

 

 

 

f(x)

 

 

f(x) = 4 x

 

4 x

 

 

2 x

 

 

 

 

 

1

 

 

 

 

soll um 1 nach links verschoben werden. Bei der Ver-

 

 

 

 

 

 

 

 

schiebung um 1 nach links ersetzen wir in der Funk-

3

2

1

 

1

2

3

x

tionsgleichung x durch x

+

1:

 

 

 

−

−

−

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

 

 

 

 

f˜ x

 

 

 

+

 

 

 

)x2

 

 

 

 

 

 

−

 

 

f (x)

 

 

 

 

1

 

 

 

 

 

 

 

 

 

f x

 

 

x

.

 

 

 

2

 

 

 

 

( ) =

 

1(x3

 

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

+

 

1

 

 

−

5

3

 

 

 

 

 

 

 

Ì

 

4

 

 

2

 

 

4

− 2

 

 

 

 

 

 

 

Beispiel 5.15 (Funktion verschieben in y)

Das Schaubild der Funktion

 

 

 

 

 

 

 

 

y

 

 

 

 

1

3

−

1

2

−

3

 

 

 

 

 

 

 

2

 

 

˜

 

 

 

 

 

 

 

 

 

f(x)

 

f(x) = 4 x

 

4 x

 

2 x

 

 

 

 

 

 

1

 

 

 

 

soll um 1 nach oben verschoben werden. Dazu müs-

 

 

 

 

 

 

 

 

sen wir lediglich den Wert 1 zur Funktionsgleichung

3

2

1

 

1

2

3

x

addieren:

 

 

 

 

 

 

 

 

 

 

−

−

−

1

 

 

 

 

f˜ x

 

 

 

 

1

 

 

 

 

 

 

 

 

−

 

 

f (x)

f x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

( ) =

 

1(x3) +1 x2

−

3 x

+

1.

 

 

 

−

 

 

 

Ì

=

 

4

−

4

 

2

 

 

 

 

 

 

 

 

Eine Skalierung ist eine Abbildung, bei der die Werte mit einem konstanten Faktor multipliziert werden. Bei einer Funktion können sowohl die x-Werte als auch die y-Werte skaliert werden.

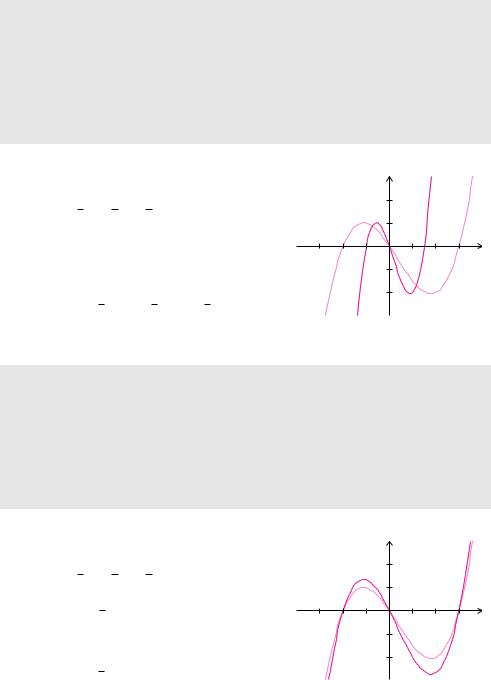
5.1 Einführung

165

Definition 5.8 (Skalierung in x-Richtung)

Definiert man eine neue Funktion f˜, indem man in der Funktion f die Variable x durch a x ersetzt

f˜(x) = f(a x),

dann entsteht das Schaubild der neuen Funktion f˜ durch Skalierung des Schaubildes von f in Richtung der x-Achse. Für a > 1 wird das Schaubild gestaucht, für 0 < a < 1 wird es gedehnt. Negative a-Werte erzeugen zusätzlich eine Spiegelung an der y-Achse.

Beispiel 5.16 (Funktion skalieren in x)

Die Funktion

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

f(x) =

1

3

−

 

1

 

2

−

3

 

 

 

 

 

 

 

 

 

 

 

2

˜

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f(x)

 

 

 

4 x

 

 

4 x

 

 

2 x

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

soll um den Faktor 2 in x skaliert werden. Dazu er-

 

 

 

 

 

 

 

setzen wir x durch 2 x in der Funktionsgleichung:

3

2

1

1

2

3

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

−

−

 

 

 

 

f˜ x

 

f

 

2 x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−1

 

 

 

 

( ) =

 

1(

 

2 x)

3

 

1

(

2 x

)

2

−

3

2 x

)

 

 

−2

 

 

f (x)

 

=

 

4

(

 

 

)

 

−

 

 

(

 

 

 

 

 

 

 

 

 

=

2

x3

−

x2

− 3

x.

 

 

 

 

 

 

 

 

 

 

 

 

Ì

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Definition 5.9 (Skalierung in y-Richtung)

Definiert man eine neue Funktion f˜, indem man die Funktion f mit dem konstanten Faktor a multipliziert

f˜(x) = a f(x),

dann entsteht das Schaubild der neuen Funktion f˜ durch Skalierung des Schaubildes von f in Richtung der y-Achse. Für a > 1 wird das Schaubild gedehnt, für 0 < a < 1 wird es gestaucht. Negative a-Werte erzeugen zusätzlich eine Spiegelung an der x-Achse.

Beispiel 5.17 (Funktion skalieren in y)

Die Funktion

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

f(x) =

1

3

−

1

 

2

−

3

 

 

 

2

 

˜

 

 

 

 

 

 

f(x)

4 x

 

4 x

 

2 x

 

 

1

 

 

 

soll um den Faktor 4 in y skaliert werden. Dazu wird

−3 −2 −1

 

 

3 x

 

 

 

3

 

 

 

 

 

 

 

 

1

2

die Funktionsgleichung mit diesem Faktor multipli-

−1

 

 

 

ziert:

 

 

 

 

 

 

 

 

 

 

 

 

f (x)

 

f˜ x

 

 

4 f

x

)

 

 

 

 

 

−2

 

 

 

( ) =

 

3x3(

 

x2

−

6

x.

 

 

 

Ì

 

=

3

− 3

 

 

 

 

 

166

5 Funktionen

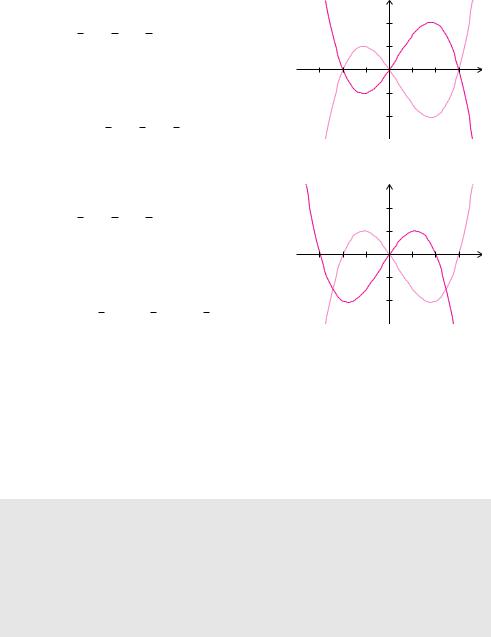
Ein wichtiger Spezialfall der Skalierung ist die Achsenspiegelung. Bei einer Spiegelung an der x-Achse skaliert man die y-Werte und bei einer Spiegelung an der y-Achse skaliert man die x-Werte mit dem Faktor −1.

Beispiel 5.18 (Funktion spiegeln an x-Achse)

Die Funktion

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

˜

 

 

1

 

 

1

 

−

3

 

 

 

 

 

 

 

 

 

f(x)

 

 

3

 

2

 

 

 

 

 

 

 

2

 

 

 

 

f(x) = 4 x

 

− 4 x

 

2 x

 

 

 

 

 

 

 

1

 

 

 

 

soll an der x-Achse gespiegelt werden. Dazu multi-

 

 

 

 

 

 

 

 

man die Funktionsgleichung mit

−

1:

3

2

1

1

2

3

x

pliziert f˜ x

 

 

f x

 

 

 

 

 

 

−

−

−

−1

 

 

 

 

( ) = −

1(x3)

1 x2

+

3 x.

 

 

 

 

 

−2

f (x)

 

Ì

=

−

4

+ 4

 

2

 

 

 

 

 

 

 

 

 

Beispiel 5.19 (Funktion spiegeln an y-Achse)

Die Funktion

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

1

3

−

1

2

 

3

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

f(x) = 4 x

 

4 x

 

− 2 x

 

 

 

 

 

 

 

 

 

 

1

f˜(x)

 

 

soll an der y-Achse gespiegelt werden. Dazu ersetzt

 

 

 

 

 

 

 

 

der Funktionsgleichung x durch

−

x:

3

2

1

1

2

3

x

man in f˜ x

f

x

 

 

 

 

 

 

 

 

−

−

−

−1

 

 

 

 

( ) =

 

1(− x)

3

1

x

)

2

−

3

 

x

 

 

 

−2

f (x)

 

 

 

=

 

4 (− )

 

− 4 (−

 

 

2

(− )

 

 

 

 

 

 

 

 

= −

1

 

3

−

1

 

2

+

3

 

 

x

 

 

x

 

 

x.

Ì

4

 

4

 

2

Translation und Skalierung sind Spezialfälle eines allgemeinen Prinzips, der sogenannten Komposition von Funktionen. Bei einer Komposition wird eine Funktion in eine andere Funktion eingesetzt. Ein Beispiel für eine verkettete Funktion ist der Heizölpreis. Der Rohölpreis wird in US-Dollar angegeben. Wir bezahlen unser Heizöl aber in Euro. Für uns ist somit die Verkettung der beiden Funktionen Ölpreis in Abhängigkeit vom US-Dollar und US-Dollar in Abhängigkeit vom Euro entscheidend.

Definition 5.10 (Komposition)

Unter der Komposition der Funktionen g und h versteht man die Nacheinanderausführung

f(x) = g(h(x)), f = g ○ h

der beiden Funktionen. Man wendet die äußere Funktion g auf das Ergebnis der inneren Funktion h an und erhält somit die zusammengesetzte Funktion f.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности