
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis
82 |
3 Vektoren |
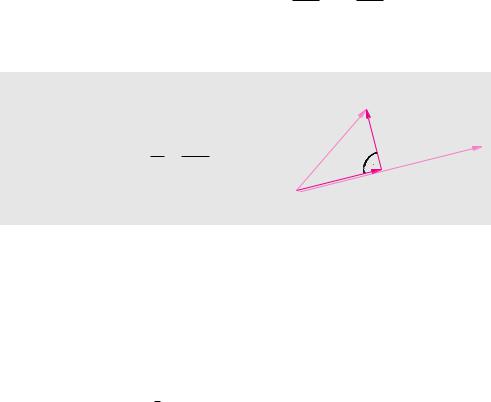
Durch Skalarprodukte lassen sich Vektoren projizieren. Die senkrechte Projektion eines Vektors b in Richtung eines Vektors a ist durch zwei Eigenschaften festgelegt. Zum einen verläuft die Projektion in Richtung des Vektors a. Zum anderen hat die Projektion die Länge des Vektors b multipliziert mit dem Kosinus des eingeschlossenen Winkels. Es gilt also
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
b a |
|
|
|
a |
b |
|
|||
ba |
|
b |
|
cos |
|
a, b |
|
ea |
|
b |
|
cos |
|
a, b |
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
2 |
a. |
= S |
S |
( |
) |
= S |
S |
( |
) S |
a |
S |
= |
|
S |
a |
S |
= |
S |
||||||||||||||
|
|
|
|
|
|
|
|
|
S S |
|
S |
|
|
|||||||||||||||||
Dabei haben wir den Einheitsvektor ea in Richtung des Vektors a verwendet.
Definition 3.8 (Senkrechte Projektion in Richtung eines Vektors)
Die senkrechte Projektion des Vektors b in
Richtung des Vektors a ist definiert durch |
|
|
b |
||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
a |
b |
|
|
|
− |
|
ba |
|
b |
|
cos |
|
a, b |
|
|
|
a. |
b |
ba |
b |
||||
= S |
S |
( |
) S |
a |
S |
= |
S |
a |
2 |
a |
|||||||
|
|
|
|
|
S |
|
|
|
|
|
|||||||
a
Diese Projektion ist ein Vektor in Richtung des
Vektors a mit der Länge SbS cos (a, b).
Die senkrechte Projektion ba des Vektors b in Richtung des Vektors a bezeichnet man auch als Parallelkomponente von b in Richtung von a. Entsprechend bezeichnet b − ba die Normalkomponente. Auch an dieser Stelle soll nochmals der Hinweis erfolgen, dass durch Vektoren nicht dividiert werden kann. Insbesondere können die Vektoren a in der Formel in Definition 3.8 nicht gekürzt werden!
Beispiel 3.6 (Senkrechte Projektion in Richtung eines Vektors)
Der Vektor a besitzt die Länge 4 und der Vektor b die Länge 2. Der Winkel zwischen den beiden Vektoren beträgt 30○. Aus diesen Angaben können wir die senkrechte Projektion des Vektors b in Richtung des Vektors a berechnen:
√
ba |
|
2 cos 30○ |
1 |
3 |
a. |
Ì |
||||
|
4 a |
4 |
|
|||||||
|
= |
|
|
|
|
= |
|
|
|
|
3.2.4 Vektorprodukt
Wir gehen nun der Frage nach, wie man einen Vektor bestimmt, der auf zwei vorgegebenen Vektoren senkrecht steht. Dieses Problem wird durch das sogenannte Vektorprodukt gelöst. Wenn wir nur Vektoren betrachten, die alle in einer Ebene liegen, ergibt diese Fragestellung keinen Sinn. Wir betrachten in diesem Abschnitt deshalb nur Vektoren im dreidimensionalen Raum.
3.2 Vektorrechnung ohne Koordinaten |
83 |
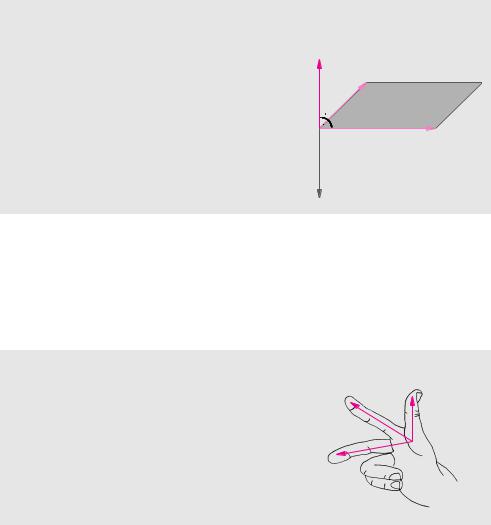
Definition 3.9 (Vektorprodukt, Kreuzprodukt)
Das Vektorprodukt oder Kreuzprodukt der beiden Vektoren a und b ist ein Vektor c = a × b mit folgenden Eigenschaften:
L |
Die Länge von c entspricht der Fläche |
des von a und b aufgespannten Parallelo- |
|
|
gramms. |
LDer Vektor c steht senkrecht auf a und b.
LDie Vektoren a, b und c bilden in dieser Reihenfolge ein Rechtssystem.
a × b
× b
a(− )b ×
b
a
Für das Vektorprodukt verwendet man die Sprechweise „c gleich a kreuz b“. Im Gegensatz zum Skalarprodukt ergibt das Vektorprodukt aus zwei Vektoren keine Zahl, sondern einen Vektor. Die erste Bedingung in Definition 3.9 legt die Länge des Vektors c eindeutig fest. Aus der zweiten Bedingung ist die Richtung festgelegt, allerdings noch nicht eindeutig. Es bleiben zwei Alternativen: nach oben oder nach unten. In der Mathematik bezeichnet man diese beiden Alternativen als Rechtsoder Linkssystem. Eine eindeutige Festlegung erreicht man durch die Forderung nach einem Rechtssystem.
Rechtssystem
Mit der Rechten-Hand-Regel kann man überprüfen, ob die drei Vektoren a, b und c in dieser Reihenfolge ein Rechtssystem bilden. Wenn der Vektor a in Richtung des Daumens und der Vektor b in Richtung des Zeigefingers zeigt, dann muss der Vektor c für ein Rechtssystem in Richtung des Mittelfingers zeigen.
b
c
a
Der Flächeninhalt des von den beiden Vektoren a und b aufgespannten Parallelogramms lässt sich aus der Länge der beiden Vektoren und dem eingeschlossenen Winkel berechnen. Ein Parallelogramm hat denselben Flächeninhalt wie ein Rechteck mit entsprechender Höhe. Die Länge der Grundseite des Rechtecks ergibt sich aus dem Betrag des Vektors a. Die Höhe des Rechtecks h = SbS sin (a, b) ermitteln wir aus der Länge des Vektors b und dem Winkel zwischen a und b. Der Flächeninhalt des von den beiden Vektoren a und b aufgespannten Dreiecks ist halb so groß wie die Fläche des entsprechenden Parallelogramms.

84 |
3 Vektoren |
Vektorprodukt und Fläche
Das von den beiden Vektoren a und b aufgespannte
L |
Parallelogramm hat den Flächeninhalt |
|
L |
Aj = Sa × bS = SaS SbS sin (a, b), |
b |
Dreieck hat den Flächeninhalt |
α |
AQ = 1 Sa × bS = 1 SaS SbS sin (a, b).
22
Beispiel 3.7 (Vektorprodukt)
h = |b| sin α
a
Der Vektor a besitzt die Länge 2 und der Vektor b die Länge 3. Der Winkel zwischen den Vektoren beträgt 60○. Dann hat das Vektorprodukt die Länge
Sa × bS = 2 3 sin 60○ = 2 3 2 |
√3 = 3√3. |
Ì |
||||
1 |
|
|
|
|
|
|
Wenn die beiden Vektoren a und b senkrecht aufeinander stehen, erhalten wir
Sa × bS = SaS SbS sin 90○ = SaS SbS.
Geometrisch ist in diesem Fall das Parallelogramm ein Rechteck, dessen Fläche man aus dem Produkt der Längen der beiden Seiten berechnet. Falls das Vektorprodukt der Vektoren a und b den Nullvektor ergibt, dann muss die Länge des Vektorproduktes null sein:
Sa × bS = SaS SbS sin (a, b) = 0.
Es gibt dafür drei mögliche Ursachen: Die Länge des Vektors a ist null, die Länge des Vektors b ist null oder der Sinus des Winkels ist null. Der Sinus wird bei den Winkeln 0○ und 180○ null, also genau dann, wenn die beiden Vektoren parallel oder antiparallel sind.
Vektorprodukt ergibt Nullvektor
Wenn das Vektorprodukt der beiden Vektoren a und b den Nullvektor ergibt, dann
Lsind die beiden Vektoren a und b parallel oder antiparallel oder
Leiner der beiden Vektoren a oder b ist der Nullvektor.
Es ist unbedingt zu beachten, dass das Kreuzprodukt nicht kommutativ ist. Beim Kreuzprodukt der beiden Vektoren a und b kommt es auf die Reihenfolge an. Wenn man die Reihenfolge der beiden Vektoren vertauscht, dann liefert das Kreuzprodukt einen Vektor, der in die entgegengesetzte Richtung zeigt: b × a = −(a × b). Das liegt daran, dass nun die Vektoren b, a und b × a in dieser Reihenfolge ein Rechtssystem bilden.

3.2 Vektorrechnung ohne Koordinaten |
85 |
Die Skalierung einer der beiden Vektoren a oder b mit dem Skalar λ hat keine Auswirkung auf die Richtung des Kreuzprodukts. Die Fläche des Parallelogramms ändert sich ebenfalls um den Faktor λ.
Satz 3.4 (Rechenregeln für das Vektorprodukt)
Für beliebige Vektoren a, b, c und Skalare λ gilt:
L |
a |
× |
b |
= − ( |
a |
× |
b |
) |
|
|
|
L ( |
λ a |
) × |
b |
= |
a |
× ( |
λ b |
) = |
λ |
( |
a |
× |
b |
) |
||
L |
b a |
+ |
|
|
|
|
+ |
|
× |
|
|
|
|
|
|
|
|
|||||||||||
|
× ( |
|
c |
) = |
a |
× |
b |
a |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Die letzte Rechenregel in Satz 3.4 beschreibt ein Distributivgesetz und garantiert, dass man auch beim Vektorprodukt Klammern ausmultiplizieren darf. Auf einen Nachweis dieses Distributivgesetzes verzichten wir.
Satz 3.5 (Entwicklungssatz)
Für beliebige Vektoren a, b und c gilt
a × (b × c) = (a c) b − (a b) c.
Das doppelte Kreuzprodukt a × (b × c) steht senkrecht auf einem Vektor, der senkrecht auf den beiden Vektoren b und c steht. Also verläuft a × (b × c) komplett in der Ebene, die von den beiden Vektoren b und c aufgespannt wird, und es gilt
a × (b × c) = λ b + µ c.
Der Nachweis, dass sich die Faktoren λ und µ, wie in Satz 3.5 behauptet, aus den Skalarprodukten berechnen lassen, erfordert jedoch eine längere Herleitung, die wir hier nicht darstellen.
In Koordinatendarstellung lassen sich die Skalare λ und µ aus Satz 3.5 auch mithilfe linearer Gleichungssysteme bestimmen, siehe Beispiel 3.15.
3.2.5 Spatprodukt
Mithilfe einer geeigneten Kombination aus Kreuzprodukt und Skalarprodukt lassen sich Volumina berechnen. Zur Festlegung eines Volumens benötigen wir mindestens drei Vektoren, die nicht in einer gemeinsamen Ebene liegen. Deshalb betrachten wir wie im letzten Abschnitt auch in diesem nur Vektoren im Raum.
86 |
3 Vektoren |
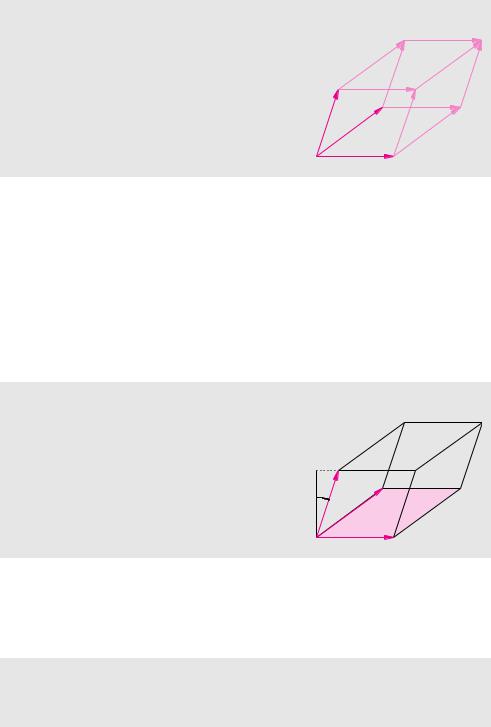
Definition 3.10 (Spat, Parallelepiped)
Drei Vektoren a, b und c, die nicht in einer Ebene liegen, spannen einen Spat oder ein Parallelepiped auf. Jeder Vektor definiert genau vier der insgesamt zwölf Kanten. Dadurch verlaufen jeweils vier Kanten parallel und sind gleich lang. Gegenüberliegende Seiten werden durch deckungsgleiche Parallelogramme begrenzt.
a
|
c |
|
|
a |
b |
|
|
|
c |
|
a |
|
b |
|
b
c a
b
c
Ziel ist nun, eine Formel für die Berechnung des Volumens des Spats, der aus den drei Vektoren a, b und c aufgespannt wird, herzuleiten. Der Flächeninhalt A der Grundfläche des Spats beträgt A = Sb × cS. Zur Berechnung des Volumens benötigen wir noch die Höhe h. Die Höhe h hängt von der Länge des Vektors a und dem Winkel α, den der Vektor a mit der zu b und c orthogonalen Richtung bildet, ab. Es ist also h = SaS cos α. Insgesamt erhalten wir somit für das gesuchte Volumen
V = Sb × cS SaS cos α = SaS Sb × cS cos α.
Da α der Winkel zwischen dem Vektor a und dem Vektor b × c ist, gilt außerdem
a (b × c) = SaS Sb × cS cos α.
Das Volumen lässt sich also als Skalarprodukt eines Kreuzproduktes berechnen.
Satz 3.6 (Volumen eines Spats)
Für das Volumen V eines Spats, der von den drei Vektoren a, b und c aufgespannt wird, gilt die Formel
V = Sa (b × c)S = SaS Sb × cS S cos αS .
Dabei ist α der Winkel zwischen dem Vektor a und dem Vektor b × c.
α |
a |
|
|
cos |
c |
||
α |
|||
|
|||
|a| |
|
||
|
b |
||
|
|
Für Winkel α größer als 90○ wird der Kosinus negativ. Die drei Vektoren a, b und c spannen dann immer noch einen Spat auf. Allerdings bilden die drei Vektoren in diesem Fall ein Linkssystem. Ein Volumen ist aber immer eine positive Größe. Um alle Fälle abzudecken, braucht man in der Formel aus Satz 3.6 deshalb die Beträge.
Definition 3.11 (Spatprodukt)
Das Spatprodukt [a, b, c] von drei Vektoren a, b und c ist definiert durch
[ a, b, c] = a (b × c) .
