
- •1 Grundlagen
- •1.1 Logik und Mengen
- •1.1.1 Aussagenlogik
- •1.1.2 Mengen
- •1.2 Zahlen
- •1.2.1 Natürliche Zahlen
- •1.2.2 Ganze Zahlen
- •1.2.3 Rationale Zahlen
- •1.2.4 Reelle Zahlen
- •1.2.5 Ordnung
- •1.2.6 Intervalle
- •1.2.7 Betrag und Signum
- •1.2.8 Summe und Produkt
- •1.3 Potenz und Wurzel
- •1.3.1 Potenzen
- •1.3.2 Potenzgesetze
- •1.3.3 Wurzeln
- •1.3.4 Binomischer Satz
- •1.4 Trigonometrie
- •1.4.1 Trigonometrie im rechtwinkligen Dreieck
- •1.5 Gleichungen und Ungleichungen
- •1.5.1 Lineare Gleichungen
- •1.5.2 Potenzgleichungen
- •1.5.3 Quadratische Gleichungen
- •1.5.4 Wurzelgleichungen
- •1.5.5 Ungleichungen
- •1.6 Beweise
- •1.6.1 Direkter Beweis
- •1.6.2 Indirekter Beweis
- •1.6.3 Konstruktiver Beweis
- •1.6.4 Vollständige Induktion
- •1.7 Aufgaben
- •2 Lineare Gleichungssysteme
- •2.1 Einführung
- •2.2 Gauß-Algorithmus
- •2.2.1 Äquivalenzumformungen
- •2.2.2 Vorwärtselimination
- •2.2.3 Rückwärtseinsetzen
- •2.2.4 Gaußsches Eliminationsverfahren
- •2.2.5 Rechenschema
- •2.3 Spezielle Typen linearer Gleichungssysteme
- •2.3.1 Lineare Gleichungssysteme ohne Lösung
- •2.3.2 Lineare Gleichungssysteme mit unendlich vielen Lösungen
- •2.3.3 Systeme mit redundanten Gleichungen
- •2.3.4 Unterbestimmte lineare Gleichungssysteme
- •2.3.5 Überbestimmte lineare Gleichungssysteme
- •2.3.6 Homogene lineare Gleichungssysteme
- •2.3.7 Lineare Gleichungssysteme mit Parametern
- •2.4 Numerische Verfahren
- •2.4.1 Jakobi-Iteration
- •2.4.2 Gauß-Seidel-Iteration
- •2.5 Anwendungen
- •2.5.1 Produktion
- •2.5.2 Netzwerkanalyse in der Elektrotechnik
- •2.6 Aufgaben
- •3 Vektoren
- •3.2 Vektorrechnung ohne Koordinaten
- •3.2.1 Addition und Subtraktion
- •3.2.2 Skalare Multiplikation
- •3.2.3 Skalarprodukt
- •3.2.4 Vektorprodukt
- •3.2.5 Spatprodukt
- •3.2.6 Lineare Abhängigkeit und Komponentenzerlegung
- •3.3 Vektoren in Koordinatendarstellung
- •3.3.1 Koordinatendarstellung
- •3.3.2 Addition und Subtraktion
- •3.3.3 Skalare Multiplikation
- •3.3.4 Skalarprodukt
- •3.3.5 Vektorprodukt
- •3.3.6 Spatprodukt
- •3.3.7 Lineare Abhängigkeit und Komponentenzerlegung
- •3.4 Punkte, Geraden und Ebenen
- •3.4.1 Kartesisches Koordinatensystem
- •3.4.2 Parameterdarstellung von Geraden und Ebenen
- •3.4.3 Parameterfreie Darstellung von Geraden und Ebenen
- •3.4.4 Schnitte von Geraden und Ebenen
- •3.4.5 Abstände
- •3.4.6 Winkel
- •3.5 Anwendungen
- •3.5.1 Kraft
- •3.5.2 Arbeit
- •3.5.3 Drehmoment
- •3.6 Aufgaben
- •4 Matrizen
- •4.2 Rechnen mit Matrizen
- •4.2.1 Addition, Subtraktion und skalare Multiplikation
- •4.2.2 Multiplikation von Matrizen
- •4.3 Determinanten
- •4.3.1 Determinante einer (2,2)-Matrix
- •4.3.2 Determinante einer (3,3)-Matrix
- •4.3.3 Determinante einer (n,n)-Matrix
- •4.4 Inverse Matrix
- •4.4.1 Invertierbare Matrizen
- •4.4.2 Inverse einer (2,2)-Matrix
- •4.4.3 Inverse Matrix und lineares Gleichungssystem
- •4.5 Lineare Abbildungen
- •4.5.1 Matrizen als Abbildungen
- •4.5.2 Kern, Bild und Rang
- •4.6 Eigenwerte und Eigenvektoren
- •4.7 Numerische Verfahren
- •4.7.1 Potenzmethode
- •4.8 Anwendungen
- •4.9 Aufgaben
- •5 Funktionen
- •5.1 Einführung
- •5.1.2 Wertetabelle
- •5.1.3 Schaubild
- •5.1.4 Explizite und implizite Darstellung
- •5.1.6 Funktionsschar
- •5.1.7 Verkettung von Funktionen
- •5.2 Polynome und rationale Funktionen
- •5.2.1 Potenzfunktionen mit ganzen Hochzahlen
- •5.2.2 Polynome
- •5.2.3 Gebrochenrationale Funktionen
- •5.3 Eigenschaften
- •5.3.1 Symmetrie
- •5.3.2 Periode
- •5.3.3 Monotonie
- •5.3.4 Beschränktheit
- •5.4 Sinus, Kosinus und Tangens
- •5.4.2 Eigenschaften
- •5.5 Grenzwert und Stetigkeit
- •5.5.1 Zahlenfolgen
- •5.5.2 Grenzwert einer Funktion
- •5.5.3 Stetigkeit
- •5.5.4 Asymptotisches Verhalten
- •5.6.1 Exponentialfunktionen
- •5.6.2 Die e-Funktion
- •5.6.3 Hyperbelfunktionen
- •5.7 Umkehrfunktionen
- •5.7.1 Das Prinzip der Umkehrfunktion
- •5.7.2 Wurzelfunktionen
- •5.7.3 Arkusfunktionen
- •5.7.4 Logarithmusfunktionen
- •5.7.5 Area-Funktionen
- •5.8 Numerische Verfahren
- •5.8.1 Berechnung von Funktionswerten
- •5.8.2 Bisektionsverfahren
- •5.9 Anwendungen
- •5.9.1 Messwerte
- •5.9.2 Industrieroboter
- •5.10 Aufgaben
- •6.1 Steigung und Ableitungsfunktion
- •6.1.3 Ableitungsfunktion
- •6.1.5 Höhere Ableitungen
- •6.2 Ableitungstechnik
- •6.2.1 Ableitungsregeln
- •6.2.2 Ableitung der Umkehrfunktion
- •6.2.5 Zusammenfassung
- •6.3 Regel von Bernoulli-de l’Hospital
- •6.4 Geometrische Bedeutung der Ableitungen
- •6.4.1 Neigungswinkel und Schnittwinkel
- •6.4.2 Monotonie
- •6.4.3 Krümmung
- •6.4.4 Lokale Extrema
- •6.4.5 Wendepunkte
- •6.4.6 Globale Extrema
- •6.5 Numerische Verfahren
- •6.5.2 Newton-Verfahren
- •6.5.3 Sekantenverfahren
- •6.6 Anwendungen
- •6.6.1 Fehlerrechnung
- •6.6.2 Extremwertaufgaben
- •6.7 Aufgaben
- •7 Integralrechnung
- •7.1 Flächenproblem
- •7.1.1 Integralsymbol
- •7.1.2 Integral als Grenzwert von Summen
- •7.1.3 Bestimmtes Integral
- •7.2 Zusammenhang von Ableitung und Integral
- •7.2.1 Integralfunktion
- •7.2.2 Stammfunktion
- •7.2.3 Bestimmtes Integral und Stammfunktion
- •7.2.4 Mittelwertsatz der Integralrechnung
- •7.3 Integrationstechnik
- •7.3.1 Integrationsregeln
- •7.3.2 Integration durch Substitution
- •7.3.3 Partielle Integration
- •7.3.4 Gebrochenrationale Funktionen
- •7.3.5 Uneigentliche Integrale
- •7.4 Länge, Flächeninhalt und Volumen
- •7.4.1 Flächeninhalte
- •7.4.2 Bogenlänge
- •7.4.3 Rotationskörper
- •7.5 Numerische Verfahren
- •7.5.1 Trapezregel
- •7.5.2 Romberg-Verfahren
- •7.6 Anwendungen
- •7.6.2 Schwerpunkte und statische Momente ebener Flächen
- •7.7 Aufgaben
- •8 Potenzreihen
- •8.1 Unendliche Reihen
- •8.2 Potenzreihen und Konvergenz
- •8.3 Taylor-Reihen
- •8.4 Eigenschaften
- •8.5 Numerische Verfahren
- •8.5.1 Berechnung von Funktionswerten
- •8.6 Anwendungen
- •8.6.1 Normalverteilung in der Statistik
- •8.7 Aufgaben
- •9 Kurven
- •9.1 Parameterdarstellung
- •9.2 Kegelschnitte
- •9.3 Tangente
- •9.4 Krümmung
- •9.5 Bogenlänge
- •9.6 Numerische Verfahren
- •9.6.1 Bézier-Kurve
- •9.7 Anwendungen
- •9.7.1 Mechanik
- •9.7.2 Straßenbau
- •9.8 Aufgaben
- •10 Funktionen mit mehreren Variablen
- •10.1.2 Schaubild einer Funktion mit mehreren Variablen
- •10.1.3 Schnittkurven mit Ebenen und Höhenlinien
- •10.2 Grenzwert und Stetigkeit
- •10.2.1 Grenzwert einer Funktion mit mehreren Variablen
- •10.2.2 Stetigkeit
- •10.3.3 Gradient und Richtungsableitung
- •10.3.5 Höhere partielle Ableitungen
- •10.3.6 Extremwerte
- •10.4 Ausgleichsrechnung
- •10.4.1 Methode der kleinsten Fehlerquadrate
- •10.4.2 Ausgleichsrechnung mit Polynomen
- •10.4.3 Lineare Ausgleichsrechnung
- •10.5 Vektorwertige Funktionen
- •10.6 Numerische Verfahren
- •10.6.1 Mehrdimensionales Newton-Verfahren
- •10.6.2 Gradientenverfahren
- •10.7 Anwendungen
- •10.7.1 Fehlerrechnung
- •10.8 Aufgaben
- •11 Komplexe Zahlen und Funktionen
- •11.1.1 Komplexe Zahlen
- •11.1.2 Gaußsche Zahlenebene
- •11.1.3 Polarkoordinaten
- •11.1.4 Exponentialform
- •11.2 Rechenregeln
- •11.2.1 Gleichheit
- •11.2.2 Addition und Subtraktion
- •11.2.3 Multiplikation und Division
- •11.2.4 Rechnen mit der konjugiert komplexen Zahl
- •11.2.5 Rechnen mit dem Betrag einer komplexen Zahl
- •11.3 Potenzen, Wurzeln und Polynome
- •11.3.1 Potenzen
- •11.3.2 Wurzeln
- •11.3.3 Fundamentalsatz der Algebra
- •11.4 Komplexe Funktionen
- •11.4.1 Ortskurven
- •11.4.2 Harmonische Schwingungen
- •11.4.3 Transformationen
- •11.5 Anwendungen
- •11.5.1 Komplexe Wechselstromrechnung
- •11.6 Aufgaben
- •12.1 Einführung
- •12.1.3 Richtungsfeld und Orthogonaltrajektorie
- •12.2.1 Separation der Variablen
- •12.2.2 Lineare Substitution
- •12.3.3 Allgemeine Eigenschaften
- •12.4.1 Allgemeine Form
- •12.4.2 Freie Schwingung
- •12.4.3 Harmonisch angeregte Schwingung
- •12.4.4 Frequenzgänge
- •12.5.1 Eliminationsverfahren
- •12.5.2 Zustandsvariablen
- •12.5.5 Stabilität
- •12.6 Numerische Verfahren
- •12.6.1 Polygonzugverfahren von Euler
- •12.7 Anwendungen
- •12.7.1 Temperaturverlauf
- •12.7.2 Radioaktiver Zerfall
- •12.7.3 Freier Fall mit Luftwiderstand
- •12.7.4 Feder-Masse-Schwinger
- •12.7.5 Pendel
- •12.7.6 Wechselstromkreise
- •12.8 Aufgaben
- •13 Fourier-Reihen
- •13.1 Fourier-Analyse
- •13.1.1 Periodische Funktionen
- •13.1.2 Trigonometrische Polynome
- •13.1.3 Fourier-Reihe
- •13.1.4 Satz von Fourier
- •13.1.5 Gibbssches Phänomen
- •13.2 Komplexe Darstellung
- •13.2.1 Komplexe Fourier-Reihe
- •13.2.3 Spektrum
- •13.2.4 Minimaleigenschaft
- •13.3 Eigenschaften
- •13.3.1 Symmetrie
- •13.3.2 Integrationsintervall
- •13.3.3 Mittelwert
- •13.3.4 Linearität
- •13.3.5 Ähnlichkeit und Zeitumkehr
- •13.3.6 Zeitverschiebung
- •13.4 Aufgaben
- •14 Verallgemeinerte Funktionen
- •14.1 Heaviside-Funktion
- •14.2 Dirac-Distribution
- •14.3 Verallgemeinerte Ableitung
- •14.4 Faltung
- •14.5 Aufgaben
- •15 Fourier-Transformation
- •15.1 Integraltransformation
- •15.1.4 Transformation gerader und ungerader Funktionen
- •15.1.5 Darstellung mit Amplitude und Phase
- •15.2 Eigenschaften
- •15.2.1 Linearität
- •15.2.2 Zeitverschiebung
- •15.2.3 Amplitudenmodulation
- •15.2.4 Ähnlichkeit und Zeitumkehr
- •15.3 Inverse Fourier-Transformation
- •15.3.2 Vertauschungssatz
- •15.3.3 Linearität
- •15.4.3 Multiplikationssatz
- •15.4.5 Faltung
- •15.5 Periodische Funktionen
- •15.5.1 Fourier-Transformation einer Fourier-Reihe
- •15.5.3 Grenzwertbetrachtung
- •15.6 Anwendungen
- •15.6.1 Lineare zeitinvariante Systeme
- •15.7 Aufgaben
- •16 Laplace-Transformation
- •16.1 Bildbereich
- •16.2 Eigenschaften
- •16.2.1 Linearität
- •16.2.2 Ähnlichkeit
- •16.2.3 Zeitverschiebung
- •16.2.4 Dämpfung
- •16.3.2 Integration
- •16.3.3 Faltung
- •16.3.4 Grenzwerte
- •16.4 Transformation periodischer Funktionen
- •16.5 Rücktransformation
- •16.7 Anwendungen
- •16.7.1 Regelungstechnik
- •16.8 Aufgaben
- •17 z-Transformation
- •17.1 Transformation diskreter Signale
- •17.1.2 z-Transformation und Laplace-Transformation
- •17.2 Eigenschaften
- •17.2.1 Linearität
- •17.2.2 Verschiebung
- •17.2.3 Dämpfung
- •17.4 Anwendungen
- •17.4.1 Zeitkomplexität von Quicksort
- •A Anhang
- •A.1 Ableitungsregeln
- •A.2 Ableitungen
- •A.3 Potenzreihen
- •A.4 Integralregeln
- •A.5 Integrale
- •A.6 Fourier-Reihen
- •A.7 Fourier-Transformationen
- •A.8 Laplace-Transformationen
- •A.9 Griechisches Alphabet
- •A.10 Bedeutende Mathematiker
- •Literaturverzeichnis
- •Sachwortverzeichnis

502 |
12 Gewöhnliche Di erenzialgleichungen |
12.5.2 Zustandsvariablen
Mit dem Eliminationsverfahren versucht man, ein Di erenzialgleichungssystem auf eine einzige Gleichung zu reduzieren. Insbesondere bei numerischen Näherungsverfahren geht man genau den umgekehrten Weg. Ausgehend von einer einzigen Di erenzialgleichung erzeugt man durch Einführung von sogenannten Zustandsgrößen ein äquivalentes Di e- renzialgleichungssystem.
Definition 12.28 (Zustandsvariablen)
Eine beliebige Di erenzialgleichung n-ter Ordnung
f(x, x,˙ x,¨ . . . , x(n−1), x(n), t) = 0
kann man mithilfe von n Zustandsvariablen oder Zustandsgrößen
z1 t |
x t , z2 t x˙ t , z3 t x¨ t , . . . , zn t x(n−1) t |
||||||||
durch ein( |
)äquivalentes= ( ) |
Di( ) =erenzialgleichungssystem( ) ( ) = ( ) |
erster Ordnung( ) = |
darstellen:( ) |
|||||
|
|
|
z˙1 |
|
|
= |
z2 |
|
|
|
|
|
z˙2 |
|
|
z3 |
|
|
|
|
|
z1, z2, z3, . . . , zn, z˙n, t |
|
= |
0 . |
|
|
||
f |
( |
) |
|
|
|
||||
|
|
|
|
= |
|
|
|
||
Beispiel 12.39 (Zustandsvariablen)
Das Pendel aus Abschnitt 12.7.5 wird durch die Di erenzialgleichung zweiter Ordnung
m ` x¨ + k x˙ + m g sin x = 0
beschrieben. Wir führen die beiden Zustandsgrößen z1 = x und z2 = x˙ ein. Für x¨ wählen wir nun nicht eine dritte Zustandsgröße, sondern verwenden x¨ = z˙2. Dabei müssen wir unbedingt beachten, dass die beiden Zustände z1 und z2 durch die Gleichung z˙1 = z2 gekoppelt sind. Insgesamt ergibt sich ein System mit zwei Di erenzialgleichungen erster Ordnung:
z˙1 = z2 m ` z˙2 + k z2 + m g sin z1 = 0 .
Die Zustandsgrößen haben physikalische Bedeutung. Der Zustand z1 entspricht der Auslenkung und der zweite Zustand der Geschwindigkeit des Pendels. Ì
Zustandsgrößen haben bei technischen und naturwissenschaftlichen Anwendungen meistens einen physikalischen Bezug, siehe Beispiel 12.39. Im Zusammenhang mit Zustandsvariablen spricht man auch vom Zustandsraum oder vom Phasenraum und speziell bei zwei Zustandsgrößen von der Zustandsebene oder Phasenebene.
12.5 Di erenzialgleichungssysteme |
503 |
Definition 12.29 (Phasenkurven, Phasenebene und Trajektorie)
Werden zwei von der Zeit t abhängige Zustandsgrößen z1(t) und z2(t) einer Di erenzialgleichung im z1-z2-Koordinatensystem dargestellt, so spricht man von einer Phasenkurve, einer Zustandskurve oder einer Trajektorie. Die z1-z2-Ebene bezeichnet man als Phasenebene oder Zustandsebene.
Beispiel 12.40 (Freie Schwingungen in der Phasenebene)
Die Di erenzialgleichung einer freien Schwingung kann man mit den Zustandsgrößen z1 = x und z2 = x˙ als System mit zwei Gleichungen erster Ordnung darstellen:
|
|
x¨ |
+ |
2 δ x˙ |
+ |
|
2 |
= |
0 |
Ô |
z˙1 |
= |
z2 |
− |
|
|||||
Für |
|
ω0 x |
z˙2 |
|
2 δ z2 |
ω02 z1 |
||||||||||||||
δ |
= |
|
|
|
|
|
|
|
= − |
|
|
|||||||||
|
0 bestehen die Lösungen aus ungedämpften |
|||||||||||||||||||
harmonischen Schwingungen: |
|
|
|
|
|
|
||||||||||||||
|
|
z1 |
|
t |
x t |
|
|
|
C1 cos ω t |
|
C2 sin ω t |
|
||||||||
|
|
z2 |
(t) = x˙(t) = |
|
ω C1 sin ω t |
+ ω C2 cos ω t |
|
|||||||||||||
|
|
|
|
|
( ) = |
|
( ) = − |
|
|
|
+ |
|
|
|
|
|
||||
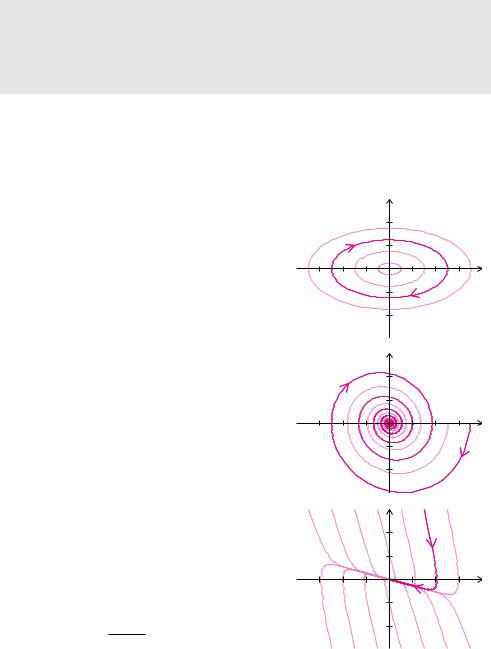
Die Phasenkurven sind Ellipsen, wobei das Verhältnis der Halbachsen durch die Kreisfrequenz ω festgelegt ist. Den Gleichgewichtspunkt (0 S 0) bezeichnet man als Wirbelpunkt. Die Abbildung zeigt den Fall ω = 12 .
Im Fall von schwacher Dämpfung, also für 0 < δ < ω0, bestehen die Lösungen aus gedämpften harmonischen Schwingungen:
z1(t) = e−δ t (C1 cos ωδ t + C2 sin ωδ t)
z2(t) = −δ e−δ t (C1 cos ωδ t + C2 sin ωδ t) + ωδ e−δ t (C2 cos ωδ t − C1 sin ωδ t) .
Die Phasenkurven sind Spiralen, die sich alle im Strudelpunkt (0 S 0) tre en.
Bei sehr starker Dämpfung, also für δ > ω0, bestehen die Lösungen aus zwei e-Funktionen mit negativem Exponenten:
z1 |
t x t |
C1 e |
λ1 t |
+ |
C2 e |
λ2 t |
|
z2 |
(t) = x˙ |
(t) = |
λ1 C1 eλ1 t |
λ2 C2 eλ2 t. |
|||
|
( ) = |
( ) = |
|
|
+ |
|
|
Der größere der beiden negativen Eigenwerte
»
λ1,2 = −δ ± δ2 − ω02
|
z2 |
|
|
|
2 |
|
|
|
1 |
|
|
−3 −2 −1 |
1 |
2 |
3 z1 |
|
−1 |
|
|
|
−2 |
|
|
|
z2 |
|
|
|
2 |
|
|
|
1 |
|
|
−3 −2 −1 |
1 |
2 |
3 z1 |
|
−1 |
|
|
|
−2 |
|
|
|
z2 |
|
|
|
2 |
|
|
|
1 |
|
|
−3 −2 −1 |
1 |
2 |
3 z1 |
|
−1 |
|
|
|
−2 |
|
|
bestimmt die Steigung der Ursprungsgeraden durch |
|
den Knotenpunkt, an den sich die Phasenkurven an- |
Ì |
nähern. |

504 |
12 Gewöhnliche Di erenzialgleichungen |
Di erenzialgleichungen, die nicht explizit von t abhängen, bezeichnet man als autonome Di erenzialgleichungen. Bei autonomen Di erenzialgleichungen ist das Richtungsfeld mit Ausnahme singulärer Punkte in allen Punkten der Phasenebene eindeutig definiert. Dadurch verläuft, mit Ausnahme singulärer Punkte, durch jeden Punkt der Phasenebene genau eine Phasenkurve. Weitere Eigenschaften ergeben sich aus dem Zusammenspiel von x und x˙.
Eigenschaften von Phasenkurven
Sind z1(t) = x(t) und z2(t) = x˙(t) Zustandsvariablen einer autonomen gewöhnlichen Di erenzialgleichung zweiter Ordnung f(x, x,˙ x¨) = 0, die also nicht explizit von t abhängt, dann haben die Phasenkurven folgende Eigenschaften:
LIn der oberen Halbebene ist x˙(t) > 0. Die Kurven verlaufen von links nach rechts.
LIn der unteren Halbebene ist x˙(t) < 0. Die Kurven verlaufen von rechts nach links.
LGeschlossene Phasenkurven entsprechen periodischen Lösungen.
LDie Phasenkurven schneiden die z1-Achse senkrecht.
Das Einführen von Zustandsvariablen erfolgt durch rein symbolisches Ersetzen, was bei jeder Di erenzialgleichung möglich ist. Selbst Systeme mit Di erenzialgleichungen höherer Ordnung können damit durch äquivalente Systeme erster Ordnung dargestellt werden.
Beispiel 12.41 (Zustandsvariablen bei Systemen)
Das Di erenzialgleichungssystem
|
|
|
x¨1 |
|
|
2 x1 |
|
x2 |
|
|
|
||
|
|
|
x¨2 |
= −2 x2 |
+ x1 |
|
|
|
|||||
besteht |
|
|
|
zwei Di erenzialgleichungen zweiter Ordnung. Mit den Zustandsgrößen |
z1 x1, |
||||||||
|
aus = |
− |
+ |
|
|
|
= |
|
|||||
z2 |
= |
x2, z3 |
= |
x˙ |
1, und z4 |
= |
x˙ |
2 erhalten wir daraus das Di erenzialgleichungssystem |
|
||||
|
|
z˙ |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
= |
|
z3 |
|
|
|
|
|||
|
|
|
z˙2 |
|
z4 |
|
|
|
|
||||
|
|
|
z˙3 |
= |
2 z1 |
z2 |
|
|
|
|
|||
|
|
|
z˙4 |
= −2 z2 |
+ z1 |
|
|
|
Ì |
||||
|
|
|
|
|
= |
− |
+ |
|
|
|
|
||
12.5.3 Lineare Systeme mit konstanten Koe zienten
Die Berechnung der Lösung eines Di erenzialgleichungssystems ist aufwendig und kann in manchen Fällen nur durch numerische Werte angenähert werden. Mit dem Prinzip der Zustandsvariablen genügt es, Di erenzialgleichungssysteme erster Ordnung zu betrachten. In diesem Abschnitt werden wir sehen, dass man Systeme, die eine ähnliche Struktur wie lineare Gleichungssysteme aufweisen, systematisch lösen kann.

12.5 Di erenzialgleichungssysteme |
505 |
Definition 12.30 (Lineares System mit konstanten Koe zienten)
Ein Di erenzialgleichungssystem, das man in der expliziten Form
x˙1 |
= |
a11 x1 |
|
a12 x2 |
|
. . . |
|
a1n xn |
|
r1 |
t |
|
x˙2 |
a21 x1 |
+ a22 x2 |
+ . . . |
+ a2n xn |
+ r2 |
(t) |
||||||
x˙n |
= |
an1 x1 |
+ |
an2 x2 |
+ |
. . . |
+ |
ann xn |
+ |
|
( ) |
|
= |
+ |
+ |
+ |
+ |
rn |
t |
) |
|||||
|
|
|
|
|
|
( |
||||||
schreiben kann, nennt man ein lineares Di erenzialgleichungssystem erster Ordnung mit konstanten Koe zienten und Störfunktionen r1(t), r2(t), . . ., rn(t).
Lineare Di erenzialgleichungen erster Ordnung mit konstanten Koe zienten sind von großer Bedeutung für Problemstellungen aus der Praxis. Di erenzialgleichungssysteme, die sich nicht als System mit konstanten Koe zienten darstellen lassen, kann man auf einem kleinen Variablenintervall durch ein System mit konstanten Koe zienten annähern. Dieses Prinzip ist so ähnlich wie die Annäherung einer Funktion mit mehreren Variablen durch ihre Tangentialebene, siehe Abschnitt 10.3.2. Einzelheiten dazu findet man beispielsweise bei [Heuser:DGL].
DGL-System in Matrixform
Ein lineares Di erenzialgleichungssystem erster Ordnung mit konstanten Koe zienten lässt sich in Matrixform darstellen:
|
x˙1 |
“ |
|
a11 |
’ x˙2 |
’ a21 |
|||
– |
|
— |
– |
|
– x˙n |
— |
= – an1 |
||
– |
|
— |
– |
|
” |
|
• |
” |
|
a12 |
. . . a1n |
|
x1 |
|
r1 |
t |
|
a22 |
. . . a2n |
“ ’ x2 |
“ ’ r2 |
(t) “ . |
|||
a11 |
. . . ann |
— – |
|
— |
– |
( ) — |
|
— – xn |
— |
+– rn |
t |
— |
|||
|
|
— – |
|
— |
– |
|
— |
|
|
• ” |
|
• |
” |
( ) • |
|
´¹¹¹¹¹¹¸¹¹¹¹¹¶ |
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
´¹¹¹¹¹¹¸¹¹¹¹¹¶ |
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶ |
|||
x˙ |
A |
x |
r |
( |
t |
) |
|
|
|
|
|
||
Beispiel 12.42 (System in Matrixform)
Das lineare Di erenzialgleichungssystem erster Ordung mit konstanten Koe zienten lässt sich in Matrixform darstellen:
x˙1 |
= |
3 x1 |
+ |
3 x2 |
Ô |
x˙ |
= Π|
3 |
− |
3 |
‘ |
x . |
|
x˙2 |
3 x1 |
5 x2 |
3 |
5 |
Ì |
||||||||
|
= |
|
− |
|
|
|
|
|
Die Darstellung linearer Di erenzialgleichungssysteme durch Matrizen ist der Schlüssel zum Erfolg. Wir werden in diesem Abschnitt erläutern, wie man die Lösung eines Differenzialgleichungssystems durch Matrizenrechung bestimmt. Satz 12.3 und Satz 12.4 gelten in entsprechender Form auch für lineare Di erenzialgleichungssysteme. Ohne die Details genauer zu betrachten, übertragen wir die Lösungsstrategie für lineare Di erenzialgleichungen auf Systeme. Das wichtigste Prinzip bei linearen Di erenzialgleichungen ist die separate Untersuchung des homogenen Systems. Man nennt ein Di erenzialgleichungssystem homogen, falls alle Störfunktionen identisch null sind.

506 |
12 Gewöhnliche Di erenzialgleichungen |
Lösungsstrategie für lineare Di erenzialgleichungssysteme erster Ordnung
Die allgemeine Lösung x eines linearen Di erenzialgleichungssystems erster Ordnung mit konstanten Koe zienten x˙ = Ax + r(t) kann man folgendermaßen bestimmen:
(1)Berechne die allgemeine Lösung xh des homogenen Systems x˙ = Ax.
(2)Berechne eine partikuläre Lösung xp des inhomogenen Systems.
(3)Addiere die homogene Lösung und die partikuläre Lösung:
x(t) = xh(t) + xp(t).
Bei linearen Di erenzialgleichungen n-ter Ordnung mit konstanten Koe zienten setzt sich die allgemeine Lösung der homogenen Gleichung aus Linearkombinationen von n Fundamentallösungen zusammen, siehe Satz 12.7 und Satz 12.8. Auch dieses Prinzip lässt sich auf Systeme übertragen.
Fundamentallösungsvektoren
Bei homogenen linearen Di erenzialgleichungssystemen erster Ordnung mit konstanten Koe zienten versucht man, Fundamentallösungsvektoren mit einem Exponentialansatz zu bestimmen:
x(t) = eλ t v .
Beim Ansatz für den Fundamentallösungsvektor ist zu beachten, dass der Vektor v nicht von t abhängt. Für den Exponentialansatz bestimmen wir die erste Ableitung und setzen x und x˙ in das homogene Di erenzialgleichungssystem ein:
x |
t |
) = |
eλ t v, x˙ |
t |
) = |
λ eλ t v |
Ô |
λ eλ t v |
= |
A eλ t v . |
|
|
( |
|
( |
|
x˙ |
t |
x t |
||||
|
|
|
|
|
|
|
|
´¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¶ |
|
± |
|
Diese Gleichung können wir mit dem Faktor e |
λ t |
( ) |
|
( ) |
|||||||
kürzen und erhalten |
|||||||||||
λ v = Av.
Dieser Typ von Gleichung ist unter dem Namen Eigenwertgleichung bekannt, siehe Definition 4.19. Die Eigenwertgleichung hängt nicht mehr von t ab und stellt deshalb eine gewaltige Vereinfachung der Ausgangsproblemstellung dar. Die Vorgehensweise zur Lösung der Eigenwertgleichung besteht aus zwei Schritten. Zunächst berechnet man die Eigenwerte und dann zu jedem Eigenwert einen passenden Eigenvektor, siehe Abschnitt 4.6.

12.5 Di erenzialgleichungssysteme |
507 |
Lösung eines homogenen linearen Systems
Die allgemeine Lösung des homogenen linearen Di erenzialgleichungssystems erster Ordnung x˙ = Ax kann man durch folgende Schritte bestimmen:
(1)Berechne alle Eigenwerte λk aus der charakteristischen Gleichung
SA − λES = 0.
(2)Bestimme zu jedem Eigenwert λk einen Eigenvektor vk:
(A − λkE) vk = 0.
Dabei sind Spezialfälle bei mehrfachen Eigenwerten und komplexen Eigenwerten zu beachten.
(3)Die allgemeine Lösung besteht aus einer Linearkombination von Fundamentallösungsvektoren:
x(t) = C1eλ1tv1 + C2eλ2tv2 + . . . + Cneλntvn.
Wir haben das Lösen eines linearen Di erenzialgleichungssystems mit konstanten Koe - zienten durch den Exponentialansatz aus dem Bereich der Funktionen in den Bereich der Algebra verlagert. Lösungen der charakteristischen Gleichung erhalten wir auch bei Systemen aus den Nullstellen eines Polynoms. Dabei treten wieder die üblichen Spezialfälle komplexer Eigenwerte und mehrfacher Eigenwerte auf.
Wenn alle Eigenwerte reell und paarweise verschieden sind, dann werden die Fundamentallösungsvektoren aus den Eigenwerten und Eigenvektoren gebildet. Im Fall eines einfachen komplexen Eigenwerts werden wir auch eine Strategie angeben. Mehrfache reelle und komplexe Eigenwerte erfordern einen erheblich tieferen Einstieg in die lineare Algebra, als wir ihn in Kapitel 4 präsentiert haben. Deshalb verzichten wir auf die vollständige Betrachtung aller Fälle.
Satz 12.13 (Einfache reelle Eigenwerte)
Falls alle Eigenwerte λ1, λ2, . . . , λn der Matrix A reell und paarweise verschieden sind, dann besteht die allgemeine Lösung des homogenen Di erenzialgleichungssystems x˙ = Ax aus einer Linearkombination von n Fundamentallösungsvektoren:
x(t) = C1eλ1tv1 + C2eλ2tv2 + . . . + Cneλntvn.
Dabei ist vk ein Eigenvektor zum Eigenwert λk.

508 12 Gewöhnliche Di erenzialgleichungen
Beispiel 12.43 (Eigenwerte und Eigenvektoren)
Wir betrachten das lineare Di erenzialgleichungssystem erster Ordung in Matrixform
x˙ = Œ |
3 |
3 |
‘ x. |
|
|
|
|
|
|
|
|||
3 |
5 |
|
|
|
|
|
|
|
|||||
Zur Bestimmung der− |
Eigenwerte berechnen wir die Lösungen der charakteristischen Gleichung |
||||||||||||
W |
3 |
− |
λ |
3 |
|
W = |
λ2 |
+ |
2λ |
− |
24 |
= |
0. |
|
|
− − |
λ |
|
|
|
|
||||||
|
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
Die beiden Eigenwerte sind somit λ1 = 4 und λ2 = −6. Einen Eigenvektor zum Eigenwert λ1 = 4 erhält man aus dem linearen Gleichungssystem
1 |
3 |
‘ v1 = 0 Ô |
v1 = Π|
3 |
‘ . |
Œ −3 |
−9 |
1 |
Eigenvektoren sind nicht eindeutig bestimmt. Deshalb kann man eine Komponente des Eigenvektors frei wählen und die andere daraus berechnen. Einen Eigenvektor zum Eigenwert λ2 = −6 erhält man aus dem homogenen linearen Gleichungssystem
Π|
9 |
3 |
‘ v2 = 0 Ô |
v2 = Π|
1 |
‘ . |
3 |
−1 |
−3 |
Das es sich um ein homogenes Di erenzialgleichungssystem handelt, benötigen wir keine partikuläre Lösung. Die allgemeine Lösung setzt sich somit aus zwei Fundamentallösungen zusammen:
x t |
|
C1e4 |
t |
|
3 |
|
C2e−6 |
t |
|
1 |
|
. |
Ì |
) = |
|
Π|
1 |
‘ + |
Π|
− |
3 |
‘ |
|||||
( |
|
|
|
|
|
|
|
Bei der Matrix in Beispiel 12.43 handelt es sich um eine symmetrische Matrix, siehe Definition 4.8. Bei symmetrischen Matrizen sind alle Eigenwerte reell und Eigenvektoren zu verschiedenen Eigenwerten stehen senkrecht zueinander, siehe Satz 4.16. Außerdem kann man immer ein vollständiges System orthogonaler Eigenvektoren angeben. Somit ist die Existenz eines Fundamentalsystems bei symmetrischen Matrizen auch im Fall mehrfacher Eigenwerte garantiert.
Komplexe Nullstellen treten bei Polynomen mit reellen Koe zienten immer als konjugiert komplexes Paar auf, siehe Satz 11.14. Die Eigenvektoren komplexer Eigenwerte sind stets komplex. Reelle Fundamentallösungen ergeben sich aus dem Realteil und dem Imaginärteil komplexer Fundamentallösungen. Dieses Prinzip kennen wir bereits von linearen Di erenzialgleichungen mit konstanten Koe zienten.
Satz 12.14 (Einfacher komplexer Eigenwert)
Falls das homogene Di erenzialgleichungssystem x˙ Ax ein Paar konjugiert komple-
xer Eigenwerte |
λ |
|
|
|
|
a |
|
|
i b |
besitzt, genügt es, |
einen komplexen Eigenvektor v |
|
zum |
||||||||||||||
|
|
1,2 |
|
|
|
|
|
|
|
|
= |
1 |
|
||||||||||||||
|
|
|
λ |
|
|
|
|
berechnen. Realteil und Imaginärteil des komplexen Fundamentallö- |
|||||||||||||||||||
Eigenwert |
|
1 |
zu |
t |
|
= |
λ1±t |
v1 |
erzeugen zwei reelle Fundamentallösungsvektoren: |
|
|
||||||||||||||||
sungsvektors z1 |
|
) = |
e |
|
|
|
|
||||||||||||||||||||
x |
1 |
t |
|
|
|
( |
|
|
|
1 |
|
, |
x |
2 |
t |
|
Im |
|
eλ1 tv |
1 |
|
. |
|
|
|||
|
|
( |
) = |
|
|
‰ |
|
|
|
|
|
Ž |
|
|
|
( |
) = |
|
‰ |
|
|
Ž |
|
|
|
||

12.5 Di erenzialgleichungssysteme |
509 |
Wieder einmal profitieren wir von der komplexen Rechnung. Die Berechnung eines einzigen komplexen Eigenwertes und Eigenvektors liefert gleich zwei Fundamentallösungsvektoren. Eine einzige komplexe Berechnung liefert hier also ein vergleichbares Ergebnis zu zwei reellen Berechnungen.
Beispiel 12.44 (Komplexe Eigenwerte und Eigenvektoren)
Die Eigenwerte des linearen Di erenzialgleichungssystems mit konstanten Koe zienten
|
x˙ = Œ |
1 |
|
4 |
‘ x |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|||
bestimmen wir−durch |
|
|
|
|
|
|
|
||||||
|
W 1 −1λ |
|
1 |
4 λ W = λ2 − 2λ + 5 = 0 Ô λ1,2 = 1 ± 2 i. |
|||||||||
Einen |
Eigenvektor− |
−zum Eigenwert λ1 |
= |
1 |
+ |
2 i erhält man aus dem linearen Gleichungssystem |
|||||||
Œ − |
2 i |
|
|
4 |
‘ v1 = 0 Ô |
|
|
|
2 i |
||||
|
1 |
|
2 i |
|
|
v1 = Œ − 1 ‘ . |
|||||||
Einen Eigenvektor− − |
zum Eigenwert λ2 |
|
|
1 |
|
2 i benötigen wir nicht. Aus dem Eigenwert λ1 und |
|||||||
dem Eigenvektor |
v1 |
ergibt sich der |
komplexe Fundamentallösungsvektor |
||||||||||
|
|
|
= |
|
− |
|
|||||||
(1+2 i)t −2 i
z1(t) = e Œ 1 ‘ .
Diesen zerlegen wir in Realund Imaginärteil:
z1 |
t |
|
e |
t |
|
cos |
|
2 t |
|
i sin |
|
2 t |
|
− |
2 i |
|
e |
t |
|
sin |
2 t |
|
i |
|
− |
2 cos |
2 t |
|
. |
) = |
|
‰ |
( |
) + |
( |
)Ž Œ |
1 |
‘ = |
|
ŒŒ |
2cos |
(2 t) |
‘ + |
Π|
sin |
(2 t) |
‘‘ |
||||||||||||
|
( |
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
( ) |
|
Das es sich um ein homogenes Di erenzialgleichungssystem handelt, benötigen wir keine partikuläre Lösung. Die allgemeine Lösung setzt sich somit aus zwei Fundamentallösungen zusammen:
x |
t |
|
C1 e |
t |
|
sin |
2 t |
|
C2 e |
t |
|
− |
2 cos |
2 t |
|
. |
Ì |
) = |
|
Π|
2cos |
(2 t) |
‘ + |
|
Π|
sin |
(2 t) |
‘ |
|||||||
|
( |
|
|
|
( ) |
|
|
|
|
( ) |
|
|
Bei linearen Di erezialgleichungssystemen mit konstanten Koe zienten kann man im Prinzip dieselben Methoden zur Bestimmung einer partikulären Lösung anwenden, wie bei linearen Di erenzialgleichungen mit konstanten Koe zienten. Wir gehen an dieser Stelle nicht auf weitere Details ein, sondern begnügen uns mit einem charakteristischen Beispiel.
Partikuläre Lösung bei linearen Systemen erster Ordnung
Eine partikuläre Lösung xp eines linearen Di erenzialgleichungssystems erster Ordnung mit konstanten Koe zienten x˙ = Ax + r(t), lässt sich in der Regel durch einen entsprechenden Störansatz berechnen. Dabei ist unter Umständen ein Resonanzansatz zu berücksichtigen. Nach dem Superpositionsprinzip kann man partikuläre Lösungen für additiv zusammengesetzte Störfunktionen getrennt ermitteln.

510 12 Gewöhnliche Di erenzialgleichungen
Beispiel 12.45 (Partikuläre Lösung)
Für das lineare Di erenzialgleichungssystem erster Ordung mit konstanten Koe zienten
x˙ = Œ 23 14 ‘ x + e−2 t Œ 210 ‘ ,
bestimmen wir zunächst die allgemeine Lösung des homogenen Systems:
2 |
3 λ |
4 |
1 |
λ |
|
λ2 |
|
6λ |
|
5 |
|
0 |
|
λ1,2 |
|
6 |
|
√ |
|
|
. |
|
|
|
|
|
|
|
36 |
20 |
|||||||||||||
W |
− |
|
− |
|
W = |
|
− |
|
+ |
|
= |
|
Ô |
|
= |
|
± |
|
2 − |
|
|
Aus den Eigenwerten λ1 = 5 und λ2 = 1 ergeben sich die Eigenvektoren:
3 |
1 |
‘ v1 = 0 Ô |
v1 = Π|
1 |
‘ , |
Π|
1 |
1 |
‘ v2 = 0 |
Ô v2 = Œ |
1 |
‘ . |
Œ −3 |
−1 |
3 |
3 |
3 |
−1 |
Die Lösung der homogenen Gleichung setzt sich aus den Fundamentallösungen zusammen:
xh(t) = C1 e |
5 t |
Π|
1 |
‘ + C2 e |
t |
Π|
1 |
‘ . |
|
3 |
|
−1 |
Zur Bestimmung einer partikulären Lösung verwenden wir einen entsprechenden Störansatz:
xp(t) = e−2 t Œ |
A |
‘ Ô |
x˙ p(t) = −2 e−2 t Œ |
A |
‘ . |
B |
B |
Obwohl die Störfunktion nur in der zweiten Koordinate vorhanden ist, benötigen wir in beiden Koordinaten einen entsprechenden Ansatz. Störansatz und Ableitung werden in das Di erenzialgleichungssystem eingesetzt:
−2 e−2 |
t |
A |
|
‘ = Œ |
2 |
|
|
1 |
‘ e−2 |
t |
Π|
A |
‘ + e−2 |
t |
Π|
0 |
‘ . |
|||||||||
|
|
ΠB |
|
3 4 |
|
B |
|
21 |
||||||||||||||||||
Nach Kürzen mit e−2 t |
ergibt sich das lineare Gleichungssystem |
|||||||||||||||||||||||||
|
4 |
|
|
1 |
‘ Œ |
A |
‘ = Œ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Œ −3 |
|
|
−6 |
B |
21 ‘ |
, |
|
|
|
|
|
|
|
|
|
|
||||||||||
das die eindeutige− − |
Lösung A |
= |
1 und B |
|
4 besitzt. Somit lautet die allgemeine Lösung |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
= − |
|
|
|
|
1 |
|
|
|
|||
x t |
) = |
C1 e5 |
t |
Π|
3 |
‘ + |
C2 e |
t |
Œ − |
1 |
‘ + |
e−2 |
t |
Œ − |
‘ |
. |
Ì |
|||||||||
|
|
1 |
|
4 |
||||||||||||||||||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
12.5.4 Lineare Di erenzialgleichung als System
Eine lineare Di erenzialgleichung mit konstanten Koe zienten der Ordnung n
an y(n) + an−1 y(n−1) + . . . + a2 y′′ + a1 y′ + a0 y = r(t)

12.5 Di erenzialgleichungssysteme |
511 |
kann man mithilfe von n Zustandsvariablen
z1 = y, z2 = y′, z3 = y′′, . . . , zn = y(n−1)
als lineares System mit konstanten Koe zienten darstellen. Aus der ursprünglichen Di e- renzialgleichung ergibt sich
an z˙n + an−1 zn−1 + . . . + a2 z3 + a1 z2 + a0 z1 = r(t).
Diese Gleichung lösen wir nach z˙n auf: |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
= − |
an |
− |
|
|
− |
|
− |
|
− |
|
|
− |
|
|
− |
|
|
= − |
|
( |
) |
z˙n |
1 |
zn |
1 |
. . . |
a2 |
z3 |
a1 z2 |
a0 z1 |
|
|||||||||||||
|
|
|
|
|
|
|
r |
t |
. |
|||||||||||||
|
|
an |
|
|
|
|
|
|
|
an |
|
|
an |
|
an |
|
an |
|||||
Die restlichen Di erenzialgleichungen ergeben sich aus der Kopplung der Zustandsgrößen:
z˙1 = z2, z˙2 = z3, . . . , z˙n−1 = zn.
Die ursprüngliche Di erenzialgleichung und das Di erenzialgleichungssystem beschreiben ein und dasselbe Problem. Die Lösungen des Problems sind durch die Eigenwerte festgelegt und die Eigenwerte ergeben sich aus den charakteristischen Gleichungen. Deshalb besitzen beide Darstellungen dieselbe charakteristische Gleichung.
Satz 12.15 (Lineare Di erenzialgleichung als Di erenzialgleichungssystem)
Jede lineare Di erenzialgleichung der Ordnung n mit konstanten Koe zienten
an y(n) + an−1 y(n−1) + . . . + a2 y′′ + a1 y′ + a0 y = r(t),
kann man mithilfe von n Zustandsvariablen z1 = y, z2 = y′, z3 = y′′′, . . ., zn = y(n−1) als lineares System mit konstanten Koe zienten darstellen:
|
’ |
0 |
1 |
0 |
|
|
0 |
|||
|
0 |
0 |
1 |
|
0 |
|||||
z˙ |
– |
0 |
0 |
0 |
|
|
1 |
|||
|
– |
|
|
|||||||
|
– |
|
|
|
|
|
|
|
|
|
|
– |
|
a0 |
|
a1 |
|
a2 |
|
|
an 1 |
|
= – |
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
n |
|
n |
|
− |
|
|
– |
|
|
|
|
|
|
|||
|
– |
− |
|
− |
|
− |
|
|
− |
|
|
” |
an |
a |
a |
an |
|||||
|
|
|
|
|
|
|
||||
“ |
’ |
0 |
“ |
0 |
|||
— z |
– |
0 |
— . |
— |
– |
|
— |
— |
– |
r t |
— |
— |
+ – |
— |
|
— |
– |
|
— |
— |
– |
an |
— |
— |
– |
— |
|
— |
– |
( ) |
— |
• |
” |
• |
Beide Darstellungen besitzen dieselbe charakteristische Gleichung
anλn + an−1λn−1 + . . . + a2λ2 + a1λ + a0 = 0.
Die Matrix aus Satz 12.15 bezeichnet man als Begleitmatrix. Bei numerischen Berechnungen verwendet man diese Begleitmatrix, um mithilfe von Verfahren zur Berechnung von Eigenwerten die Nullstellen eines Polynoms zu berechnen.
