Наближене розв’язування лінійної крайової задачі для диференціального рівняння другого порядку за методами гальоркіна, рітца та колокацій

Глазкова А.Ю., керівник Шинковська І.Л.

Національна металургійна академія України

Нехай дано диференціальне рівняння другого порядку та граничні умови:

,

. (1)

Розв’язок крайової задачі (1) будемо шукати у вигляді

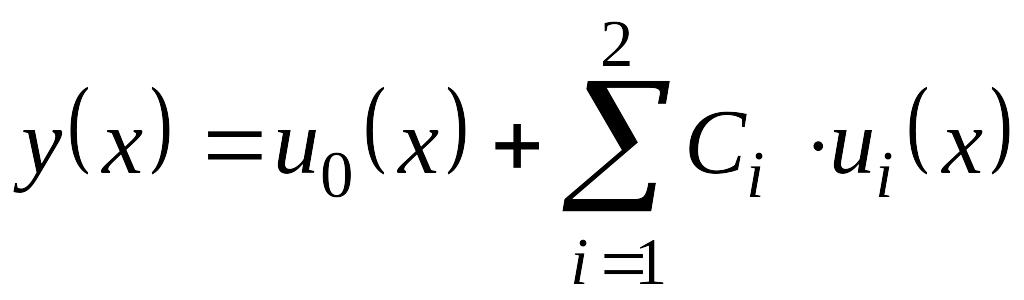, (2)

де 0,1,2 - обрана система базисних функцій, а саме 2, ,

, яка є ортогональною на відрізку .

В роботі розглядається розв’язання задачі трьома методами, окремо для двох та трьох базисних функцій. Порівняння результатів наведено у вигляді графіків.

Застосування рядів фур’є для дослідження згину тонкої жорсткої прямокутної пластини

Полякова О.Г., Дунаєв О.А., керівники доц. Чуднов К.У., ст. викл. Кочеткова І.Б.

Національна металургійна академія України

Дослідження згину пластин та оболонок має велике значення для розрахунку на міцність сучасних інженерних конструкцій (корпусів літаків, кораблів, ракет тощо). Використання гіпотез Кірхгофа-Лява зводить задачу розрахунку жорсткої пластини до розв’язання рівняння Софі Жермен-Лагранжа. Розв’язок цього рівняння отримано з використанням метода М.Леві у вигляді рядів Фур’є. Досліджено вплив на напружено-деформівний стан пластини її геометричних розмірів та умов закріплення країв.

Математична модель поточного стану матеріалу при термічній обробці

Кадильников С.В. керівники доц. Кагадій Л.П., ст. преп. Кочеткова І.Б.

Національна металургійна академія України

Кількісні значення показників якості виробів визначаються функціями стану, які залежать від властивостей матеріалу, а також показників, що характеризують метрологію вимірів математично багатофункціональну систему оцінки стану матеріалу при термічній обробці можна описати нелінійним диференціальним рівнянням першого порядку:

_,

_{де - вихідні параметри матеріалу як об’єкта досліджень, - часова стала, що характеризує глибину дослідження, - вхідні збурю вальні параметри, які залежать від умов термічної обробки.}

_{Для розрахунку перехідних процесів термообробки застосовуються операційні методи, а частинні періодичні рішення обираються у вигляді функції при впливових діях , де та - амплітуди відповідних параметрів, частота, час, мнима одиниця.}

Математична модель управління поточним станом матеріалів

Мокрицька М.В., керівники проф. Кадильникова Т.М., ас. Сушко Л.Ф.

Національна металургійна академія України

Задача управління системою стану матеріалу формується у вигляді розкладу:

, (1)

где набір випадкових коефіцієнтів; неперервні детерміновані функції, що характеризують змінення структурних параметрів матеріалу у часі; помилка моделі, яка визначається як функція похибки вимірів структурних параметрів; часовий інтервал.

Модель (1) утворює на інтервалі систему функцій Чебишева, розв’язком якої є поліноми Карліна та , що утворюють простір поточного стану, у якому гарантовано знаходяться дійсні реалізації процесів (1).

Управління системою здійснюється у моменти контролю шляхом повернення у нульове положення в границях допуску та зупинки під час виходження параметру за границю простору поточного стану.

ПІДСЕКЦІЯ ЗАГАЛЬНОЇ ТА ОРГАНІЧНОЇ ХІМІЇ